潜在类别分析LCA latent class analysis
由于论文需要用到此方法，这里做此学习记录，有需要的同学可一起学习进步。这里使用的软件为Mplus。
一、潜在类别分析的基础知识
潜在类别分析是潜在变量分析的一种，是将潜在变量理论与分类变量相结合的一种统计分析技术，是探讨存在统计学关联的分类外显变量背后的类别潜在变量的技术。ＬＣＡ的目的在于利用最少的潜在类别数目解释外显分类变量之间的关联，并使各潜在类别内部的外显变量之间满足局部独立的要求。
１）潜在变量与外显变量
潜在变量与外显变量，也称潜变量与显变量，是结构方程模型中的两种主要变量。
外显变量是指日常生活中能够直接观测、统计的变量。
潜在变量是指不能被直接精确观测，或虽能被观测但尚需通过其它方法加以综合的指标。
一个潜在变量往往对应着多个外显变量，可以看作是对应的多个外显变量的抽象和概括，外显变量则可视为特定潜在变量的反映指标。
2)连续变量与类别变量
依据统计学概念,连续变量(continuous variables)指在一定区间内可以取任意值的变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值。连续变量的测量结果是有意义的数值反应强度,例如身高几公分、体重几公斤等。在潜在变量分析中,即使被测量的结果是离散数值、无法作更精确的切割(例如家庭人数),但由于其数值具有测量大小的意义,可以进行加减乘除四则运算,也认为是连续变量的概念。
类别变量(categorical variables)是指仅仅代表某一特定类别,类别之间互有差别,但不能做四则运算的变量,例如性别、居住地区、宗教信仰、教育水平、医学上的疾病分类、牛物上的物种分类、管理学中的成功失败、对商品的满意程度等等。这些变量充斥着牛活,很容易被观察与测量,但其反映的是测量对象在本质上的类型上的差异,而非测量程度大小的概念,因此多半以人为的方式予以定义。
多半Ｗ人为的方式予以定义。
3)潜在变量分析与潜在类别分析
潜在变量分析与潜在类别分析都是研究潜在变量与外显变量关系的手段,区别在于分析变量的类型,潜在类别分析是潜在变量分析的一种特殊情况。
潜在类别模型(latent class model, LCM)是探讨LCA的模型化分析技术。
它与传统因素分析最大的不同在于变量的形式:因素分析处理的是连续变量,潜在类别模型处理的是类别变量。一个完整的LCM的建立需要经过模型的概率参数化与模型构建、参数估计与模型拟合、潜在分类三个步骤。
(1)概率参数化
潜在类别模型最突破性的原理是将类别变量的概率转换成模型的参数,亦即概率参数化(probabilistic parameterization),这其中的类别变量包括潜在变量与外显变量,所以模型中包含的概率参数也分为两类:潜在类别概率(latent classprobabilities)与条件概率(conditional probabilities)。
１）潜在类别概率
潜在类别巧率即潜在变量义所对应的参数，完整的数学形式为：
2)条件概率
在LCA的各潜在类别中,随机抽取一个样本,在外显变量上做出各种选择对应的概率称为条件概率。理解条件概率的关键有两点:
第一,需要对各外显变量进行分水平处理,同一外显变量各水平之间完全独立。
第二,分水平处理后的不同外显变量各水平之间完全独立。
在高铁旅客选择行为研究中,由前文分析可知,旅客属性、产品属性、购票行为对客流分布造成的差异是有统计关联的,即旅客选择行为中,三者之间并非相互独立,而是存在一定交叉的。所以在潜在类别模型建立之前,需要对三者所对应的外显变量进行分水平处理,并保证分水平处理后各外显变量不同水平之间彼此完全独立。
例如：①性别分为2个水平:男、女。②出行距离分为3个水平:短途、中途、长途。③购票方式分为4个水平:车站、代售点、互联网、自动售票机。
现以A.B.C分别表示性别、出行距离、购票方式,且其分别具有不同的水平: I=2,J=3,K=4,则
分别表示假设旅客属于潜在变量第T类情况下,对A外显变量选择i,对B外显变量选择j,对C外显变量选择k的条件概率:
这些条件概率类似于因素分析中的因素负荷(factor loading),用于说明各潜在类别与外显变量之间的关系,亦即可以协助研究者解释各潜在类别的内容与性质。在各潜在类别中,较大的条件概率值,表示潜在变量对于该外显变量的影响较强，比重较大。
考虑到某一潜在类别下任意一个旅客必然会在A这一外显变量的不同水平之间做出唯一的选择,因此A对应的1个水平的条件概率之和为1.00,同理, B、C分别对应的JK个水平的条件概率之和也为1.00:
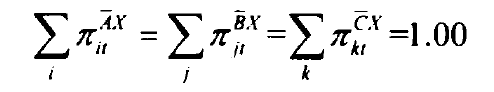
(2)模型构建
在完成概率参数化过程以后,进行模型的构建。模型的目标函数是求一个联,合概率(jointprobability) P(A=i,B=j,C=k),用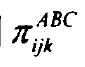
表示,含义为旅客对A外显变量选择i、对B外显变量选择j的同时,对C外显变量选择k的联合概率。出由于各外显变量不同水平之间完全独立,所以目标函数的最终形式为:
一般而言,潜在类别概率表示了潜在变量X的不同水平的比重,即表示各潜在类别群体大小,而条件概率则更多用于解释各潜在类别的属性特征及意义。
参数估计与模型拟合
(1)极大似然估计量
在LCM中,模型求解的方法主要是极大似然法,至于迭代过程中所使用的算法有EM (expectation-maximization)、NR (Newton-Raphson)等不同算法,其中LCM中广泛使用的是EM算法,其最大优点是具有不受初始值选择影响的稳健性,缺点则是迭代次数较多,且不提供标准误差的估计数。对于一个具有T个潜在类别的潜在变量X的LCM模型,极大似然估计函数如下:
初始值导出后，反复估算得到新的估计数，直到估计数的变化小于一定的程度(低于容忍值tolerance)才停止估计,即LCM参数估计迭代达成收敛。所获得的联合概率估计数即可应用于模型适配检验。
(3)模型适配检验
LCM适配检验方法主要有Pearsonx2、似然比(likelihood ratio, LR)卡方统计量G2,以及AIC指标(Akaike information criterion)和BIC指标(Bayesianinformation criterion),一般认为,各项适配指标均以越小越好,当样本数超过数千人以上或是模型的参数数目较少时,采取BIC指标检验为宜。
潜在分类
分类是LCA的最终目的。潜在类别分析的最后步骤,是将所有的旅客分类到适当的潜在类别中去,分类的原理是利用贝氏理论。假设某一旅客对前文A、B、C三个外显变量的选择行为分别为i、j、k,依据潜在类别模型可以分别求得该旅客属于1至T类潜在类别的概率
(其中t=1,2， …T),此求出该旅客属于第t类的后验概率：
利用公式4-6求出各该旅客属于各个潜在类别的后验概率后,根据后验概率大小判断该旅客应归入的潜在类别,
例如,第t类的后验概率最大,则此旅客归为第t类。对所有旅客进行后验概率的计算与比较,从而实现分类的目的。
为什么要使用该方法？什么情况可使用此方法？
优势
与传统聚类分析的比较
传统的聚类分析方法存在一些固有的不足之处,以最常用的K-means聚类分析为例,其存在以下缺点
- K-means算法随意选择初始的聚类中心,使得聚类效果时好时坏。
2)要事先制定K的值,人为决定存在较大误差。
3)当数据量不多时,输入的数据的顺序不同会导致结果不同。
4)无法确定哪个属性对聚类的贡献更大。
此外,传统的聚类分析方法多是在主成份分析的基础上进行聚类。而主成份分析的本质是减少变量个数、以少数变量来解释尽可能全的信息,并且通过正交变换来使得到的主成份保持独立,这就造成了必然有缺失的信息不能被解释。
LCA在目的与功能上可以看作是主成份分析与聚类分析的结合,其本质是寻找潜在的共同因素(即潜在变量),相比传统聚类分析而言,其具有以下优点:
1)不需剔除变量,保证了外显变量反映的信息的完整度。 - LCA可以对给定的类别数目建模,并比较得到最合适的模型,减少了人为指定K所造成的误差。
- LCA与输入数据的顺序、数据各变量之间的相互顺序无关。
LCA应用领域
潜在变量分析在社会科学研究领域有着重要的地位, LCA也得到了广泛的应用,例如医学、教育学、社会学、心理学等
在医学研究中,若假设心理疾病是一种潜在的特质,没有一个客观明确的诊断标准,而医生也只能通过一些外显的测量,例如对病人语言、行为方面比较,用概率的描述将诊断结果转化为潜在的特质,来界定其是否有心理疾病以及患病程度等。
在教育学领域,为了解学生对科目掌握程度的情况,通过做题测试来进行间接测量,掌握程度就是潜在变量,每个学生对每一道题给出的结果,可以作为观测统计得到的外显变量取值。
在管理学中的能力、信任、自尊、动机、成功等概念，也是人们为了理解和研究社会而建立的假设概念,并不存在直接测量的操作方法,可以作为潜在变量,通过一些问答或其他统计方法间接测量得到外显变量取值
又如假设需要调查对于某个商品的满意度, "满意度”就是潜在变量,是一个不可测量、抽象的概念,为了了解客户对于商品的满意度,就需要设计一系列的问题及指标,例如商品价格、包装、质量、购买途径等等,这些问卷上的题目,就是与“满意度”这个潜在变量对应的外显变量,是可以直接测量得到的。
推荐参考书籍
王孟成、毕向阳 潜变量建模与mplus应用进阶篇