R语言绘制逆概率加权后的基线表

基于 PS （倾向评分）的逆概率加权(IPTW )法首先由Ｒosenbaum作为一种以模型为基础的直接标准化法提出，属于边际结构模型。简单来说，就是把许多协变量和混杂因素打包成一个概率并进行加权，这样的话，我只用计算它的权重就可以了，方便了许多。那么，如何将多个协变量的影响用一个倾向评分值来表示呢? 即如何估计倾向评分值呢? 根据 Rosen-baum 和 Rubin 的定义:倾向评分值为在给定一组协变量(X i )条件下，研究对象 i(i =1，2，…N)被分配到某处理组或接受某暴露因素(Z i =1)的条件概率。

采用 logistic 回归模型估计倾向评分值具有模型
简单、容易实现、可直接得到倾向评分值、结果易于解释等显著优势。
我们拿logistic 回归做例子：
logistic 回归是最早提出的估计倾向评分值的方法，由于其原理为人们所熟悉且容易实现，
也是目前最常用的估计方法。logistic 回归模型如下:

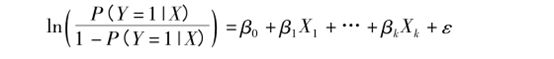
假设为二元logistic 回归，右边一系列混杂因素的方程会生成一个0-1之间的目标事件时间发生的概率，概率越大代表事件发生的可能性越大，这样就等于把多个混杂因素做成了一个综合评分来表示。逆概率加权（IPTW）是利用倾向性评分的倒数来处理数据间混杂的一种方法。Robins等给出的加权系数(形)计算方法是：处理组观察单位的权数Wt=1／PS，对照组观察单位的权数Wc=1／(1一PS)。PS为观察单位的倾向评分值。此方法得到的
人群往往与原来人群的数量不同，因此虚拟人群各变量的方差大小可有变化，而且有较低 PS 的处理组对象与有较高 PS 的非处理组对象将会获得很大的权重。由于非常大的权重会诱导不稳定性。Heman等人对计算方法进行调整，将整个研究人群的处理率和非处理率加入公式调整后得到稳定权数(stabilized weights)。具方法是：处理组观察单位的权数Wt=Pt／PS，对照组观察单位的权数Wc=(1–Pt)／(1–PS)。 目前蛮多文章使用稳定权重。
在既往文章中，我们已经介绍了怎么使用R和SPSS进行逆概率加权分析，后台有粉丝问，如何绘制加权后的基线表，如下图，加权后基线资料基本上被配平

今天我们通过R来演示一下如何绘制加权后的基线表，继续使用我们的早产数据（公众号回复：早产数据，可以获得该数据），我们先导入R包和数据

library(tableone)
library(survey)
bc<-read.csv("E:/r/test/zaochan.csv",sep=',',header=TRUE)
bc <- na.omit(bc)

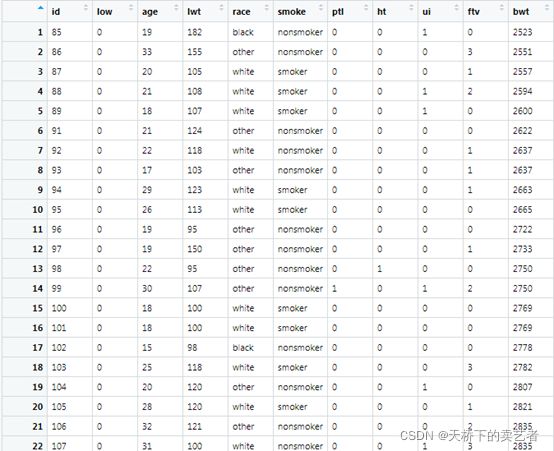
这是一个关于早产低体重儿的数据（公众号回复：早产数据，可以获得该数据），低于2500g被认为是低体重儿。数据解释如下：low 是否是小于2500g早产低体重儿，age 母亲的年龄，lwt 末次月经体重，race 种族，smoke 孕期抽烟，ptl 早产史（计数），ht 有高血压病史，ui 子宫过敏，ftv 早孕时看医生的次数
bwt 新生儿体重数值。
我们先把分类变量转成因子

bc <- na.omit(bc)
bc$race<-ifelse(bc$race=="black",1,ifelse(bc$race=="white",2,3))
bc$smoke<-ifelse(bc$smoke=="nonsmoker",0,1)
bc$low<-factor(bc$low)
bc$race<-factor(bc$race)
bc$ht<-factor(bc$ht)
bc$ui<-factor(bc$ui)

假设我们研究的是有无高血压（ht）对生出低体重儿（low）的影响，我们先绘制一个还没有加权的患者基线表

dput(names(bc))##输出变量名
allVars <-c("age", "lwt", "race", "smoke", "ptl", "ht", "ui", 
            "ftv", "bwt")###所有变量名
fvars<-c("race", "smoke","ht","ui")#分类变量定义为fvars
tab2 <- CreateTableOne(vars = allVars, strata = "low" , data = bc, factorVars=fvars,
                       addOverall = TRUE )###绘制基线表
print(tab2)#输出表格

我们注意到，上图中有3个指标P是小于0.05的，bwt属于结局指标，lwt体重属于基线指标。
我们先建立回归方程生成预测值

pr<- glm(ht ~age + lwt + race + smoke + ptl + ui + ftv, data=bc,
         family=binomial(link = "logit"))
pr1<-predict(pr,type = "response")
summary(bc$ht)

上图显示有高血压12人，没有高血压177人，下面我们来分别生成两种权重一种是Robins等给出的加权系数(形)计算方法，

w<- (bc$ht==1) * (1/pr1) + (bc$ht==0) * (1)/(1-pr1)

另外的是Heman等人对计算方法，计算稳定权重要先生成概率（发生高血压的概率）

pt<-12/(177+12)
w1 <- (bc$ht==1) * (pt/pr1) + (bc$ht==0) * (1-pt)/(1-pr1)

生成权重后就可以绘制加权后的基线表格，这里就需要使用到survey包的svydesign函数，这是一个强大的R包，可以生成各种权重的基线表格。

bcSvy1<- svydesign(ids = ~ id, strata = ~ low, weights = ~ w,
                   nest = TRUE, data = bc)

生成后就可以使用TableOne包绘制加权表格

Svytab1<- svyCreateTableOne(vars = c( "age", "lwt", "race", "smoke", "ptl","ui", 
                                      "ftv", "bwt"),
                            strata = "low", data =bcSvy1 ,
                            factorVars = c("race", "smoke","ht","ui"))
Svytab1

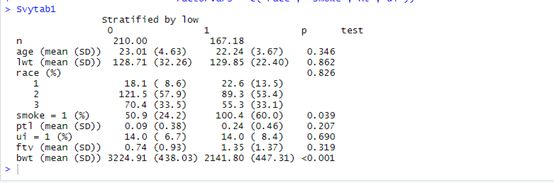
由上图可知经过加权后，每组病例数已经发生了改变，lwt这个基线治疗已经被配平，使得两组患者的比较更加具有可比性，下面我们使用Heman等人对计算方法生成权重生成基线表格

bcSvy2<- svydesign(ids = ~ id, strata = ~ low, weights = ~ w1,
                   nest = TRUE, data = bc)
Svytab2<- svyCreateTableOne(vars = c( "age", "lwt", "race", "smoke", "ptl", "ui", 
                                      "ftv", "bwt"),
                            strata = "low", data =bcSvy2 ,
                            factorVars = c("race", "smoke","ht","ui"))
Svytab2

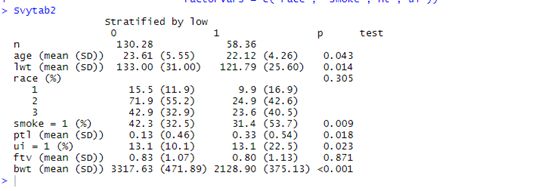
我们可以看出，针对本文章中的数据，Heman方法生成的基线表格，病例数没有Robins方法的病例数变化那么大，但是在配平基线资料上没有Robins方法配得好。并不是说Robins方法比Heman方法更好，估计在不同的数据中，两种方法各有优势。