知深行远：关于图神经网络层数加深的探索

作者 | 贺华瑞

简介

什么是GNN？

图 (Graph) 由结点和连边组成，我们把应用于图上的神经网络算法称为图神经网络 (Graph Neural Network, 简称GNN)。受启发于卷积神经网络 (Convolutional Neural Network, 简称CNN) 和图嵌入算法，GNN以图作为输入，根据“相邻的结点具有相似性”这一假设，对图中结点采用聚合其周围结点信息作为自身的表征的方式，将图中结点映射为连续向量空间中的向量，使得结构上相近的结点在嵌入空间中有相似的向量表示。

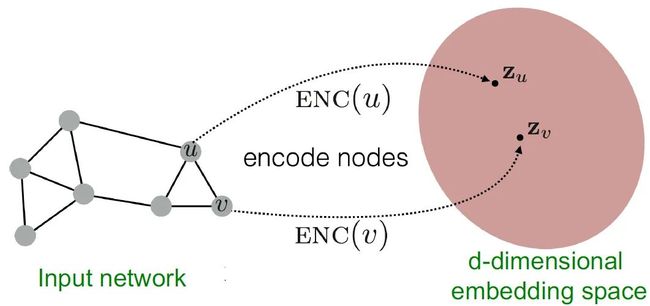图表示学习 [18]

为什么需要GNN?

对于图像、视频、音频等数据，经典的神经网络 (如CNN和RNN) 已经能够较好地处理，并且目前也已经取得了不错的效果,为什么我们还会需要GNN呢？究其原因，以上提到的数据类型属于“排列整齐”的欧几里得结构数据 (Euclidean Structure Data)，可以清晰地将它们表示为网格 (grid) 类型，对于格中任一点，总能很容易可以找出其邻居结点，就在旁边，不偏不倚。而现实生活中，除了以上提到的“规整”的网格结构数据外，还有社交网络、化合物结构图、生物基因蛋白以及知识图谱等非欧几里得结构数据 (Non-Euclidean Structure Data)。LeCun 等人 [1] 总结常见非欧几里得结构数据有流形数据 (manifolds) 和图数据 (graphs) 两种，对这些数据中的某一点，很难定义出其邻居结点来，或者不同结点的邻居结点数量是不尽相同的。

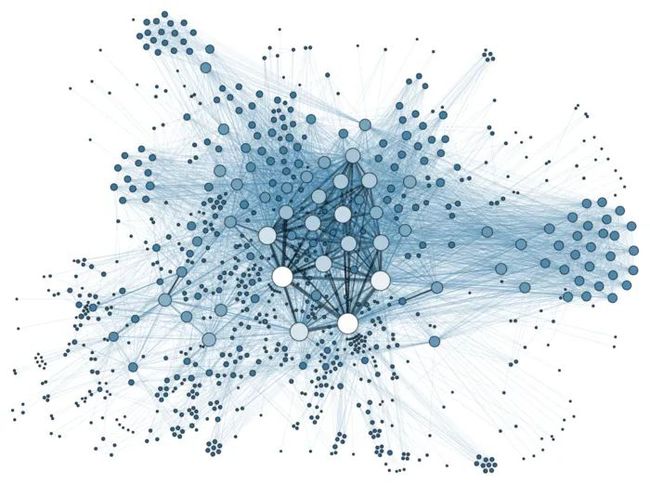manifold [19] graph

GNN的训练流程及应用

在非欧几里得结构数据上，CNN和RNN等经典深度学习模型已不再适用，而GNN就是处理图数据的一种新范式。给定一张由结点和连边组成的图作为输入，GNN的训练流程通常分三步走：（1）消息传递(message passing)；（2）邻域聚合(neighborhood aggregation)；（3）状态更新(representation update)。具体的公式在此不予详述，感兴趣的读者可参看论文 [2]。经多轮迭代训练后，GNN会为图中各结点学习到稳定的向量表示，对这些向量做简单处理，即可便捷地应用于不同的下游任务。

那么具体地，GNN可应用于哪些场景呢？有人制作了如下图所示的GNN应用树，GNN的应用范围有多宽广，由此可见一斑。

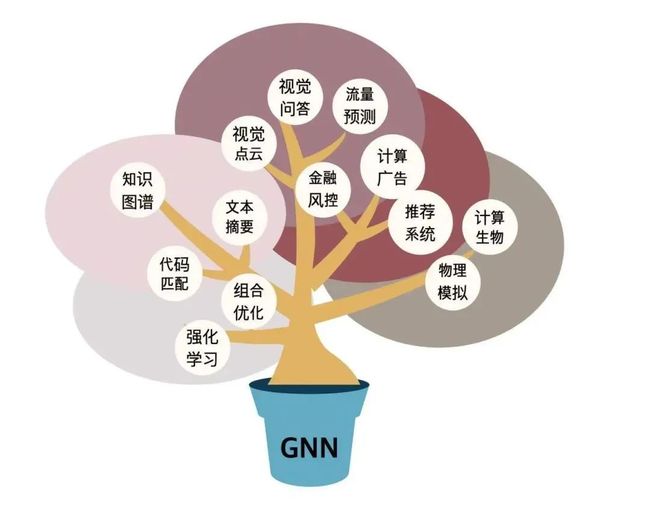GNN应用树 [20]

举例来说，国际著名的图片社交平台 Pinterest，就是GNN最成功的应用之一。用户可以收藏平台中的任何图片，并根据自己的喜好将图片放到不同的收藏夹中。鉴于每张图可能会被不同用户放入不同的收藏夹中，以每张图片和每个收藏夹为结点，其中的连边表示图片被放入某个收藏夹，据此我们得到了一个由约30亿结点和200亿连边组成的图片-收藏夹二部图(bipartite graph，也就是说连边的两端不可能同时是图片或同时是收藏夹)。

GNN在Pinterest中的应用 [18]

得到这样的图数据后，Pinterest 后台做的事就是利用GNN邻域聚合的方式（认为属于同一个收藏夹的图片是“邻居”），为每张图片生成一个向量 [3]，使得含义相似的图片在向量空间中的距离相近，从而当用户点击一张感兴趣的图片时，后台可以迅速搜索向量空间中与该图最相近的图片，并向用户推荐，借此满足用户需求，也提高了网站的点击率。注意整个过程中 Pinterest 并不需要对图片进行视觉上的训练与学习，从而大大减少了模型计算量与响应时间，甚至取得了比采用视觉模型更优越的推荐效果。

为什么需要深层的GNN？

通过前文较为轻松的入门介绍，我们对GNN已经有了大致的了解，接下来我们将继续探讨GNN的一些深层次机理。其实要说GNN是“深度”学习模型是有一些牵强的，因为在一般的结点/图分类、链接预测等任务中，GCN [4]、GAT [5]、GIN [6] 等经典的GNN模型及其变体在2~4层即可达到很好的性能表现，且在继续直接堆叠网络层数时发现性能下降的现象。根据 ResNet [7]、DenseNet [8] 等深层化神经网络模型在计算机视觉领域的成功，很自然地，我们想问GNN是否也有往深层化方向发展的需求呢？

近年来，许多学者研究了这一主题，在我看来，至少在以下两种场景中，我们是需要深层GNN的：「少标签半监督结点分类」和「少特征半监督结点分类」。具体地，前者对应有小样本文本分类问题，以每篇文章为结点，若文章之间有引用，则认为结点之间有边相连，不同于一般的基于GNN的文本分类任务，输入的图中只有少量文本有类别标签。此时，为提高分类准确率，不得不加深模型的网络层数，这是因为各结点状态更新时一般只聚合一跳邻居信息，那么网络层数即反映结点的向量表示融合了几跳内的邻居信息，当标签很少时，结点在浅层聚合过程中可能无法获取有效的标签信息，从而对分类性能造成不利影响。而第二种场景对应有推荐系统中的冷启动问题，面对缺少历史行为数据的新用户，如何为其进行个性化推荐？系统只凭借该类用户的少量注册信息（即与少量点击商品的连边）往往很难做出精准推荐，此时也需要利用深层GNN对该用户的潜在消费兴趣进行建模。

综上两种情景，GNN的网络层数某种程度上表征了各结点最终向量表示的信息来源范围，正所谓“欲穷千里目，更上一层楼”，网络层数增加后，邻域聚合的感受野也相应扩大，“知之深则行愈达”，理论上能更好地应对上述两种任务。

深层化GNN的难点在哪里？

既然GNN层数加深理想情况下会有增益，那么我们为什么还不立即行动呢？前面提到过，GCN [4]、GAT [5]、GIN [6] 等经典的GNN模型在网络层数超过2~4层时发生性能下降的现象，GNN加深的难点在哪里呢？近年来，学者们已经接连发现加深GNN面临三大障碍：过拟合 (over-fitting)、梯度消失 (gradient vanishing) 和过平滑 (over-smoothing)。前两个障碍在深度学习领域已是司空见惯，在此不做赘述，我们主要分析一下 over-smoothing 的原因。Over-smoothing 由论文 [9] 首先发现，并在论文 [10] 中被进一步分析阐明，顾名思义， over-smoothing  即是在GNN多层网络训练中，随着层数加大，图中结点的向量表示趋向于相等的现象。具体来说，可以从两个角度加以理解，首先是结点的角度，GNN结点的邻域聚合被证明其实是 Laplacian smooth 的一种特殊形式，迭代地进行 Laplacian smooth 自然导致结点层面的  over-smoothing ；其次是特征的角度，根据压缩映射原理（参考之前的文章【基础训练】压缩映射原理及其应用），迭代训练层数的增加也会导致各结点向量表示的特征维度层面的 over-smoothing 。

深层化GNN的研究脉络及未来方向

在掌握了深层化GNN面临的几大障碍后，以下将介绍目前主流的解决思路。对已有的文章进行梳理总结，我们知道现在大概存在两种加深GNN的研究思路：

• 它山之石可以攻玉，日光之下并无新事，从故纸堆中我们可以几乎可以找到一切想要的答案。既然GNN本就与CNN有剪不断理还乱的关联，我们很自然地会想到从CNN中迁移已有的研究成果，事实上这也确实奏效。如 JKNet [11] 在ResNet [7] 启发下引入强弱自适应的残差连接 ；DeepGCN [12] 从ResNet [7]、DenseNet [8] 以及 dilated CNN [13] 中汲取灵感，在各网络层间引入residual/dense connections，并采用dilated convolutions直接扩张聚合感受野；DropEdge [11] 则是受 Dropout 启发，针对图学习场景做了一些改进；NodeNorm [12] 则是从 BatchNorm [13] 一系列工作中获取思路。

• "头痛医头，脚痛医脚"，有仰望星空的怀旧派，就有脚踏实地的现实主义。有学者针对上文三大难点逐个攻破，采用 SGC [14] 克服过拟合和梯度消失，随后 Pairnorm [10] 被提出用于克服 over-smoothing 问题。Pairnorm [10] 的思想相当直接，即在目标函数中强制使相邻结点的向量表示尽量相近，非相邻结点的向量表示尽量相异。

上述两种思路皆为GNN深层化迈出了前进的一大步，做出了卓有成效的贡献，那么未来的深化GNN还有哪些可能的研究方向呢？我认为还有以下两个可能的思路：

• 面向下游任务对图数据做稀疏化处理，使得深层GNN不传播干扰信息，从而有效减缓深层化的几个障碍；

• GNN并不总是越深越好，模型应考虑数据集的特性，根据图的局部稠密性做自适应深度调节。

总结

本文简介了GNN及其应用，梳理概括了加深GNN层数的三大难点以及相应的研究思路与学术工作，并对深层化GNN未来可能的发展方向提出了畅想。GNN作为新兴模型，还有很多可供推敲之处，深层化不过是其冰山一角。毋庸置疑的是，对于GNN，还有更多瑰丽的景色在深处等待我们去发掘。

[1] Bronstein M M, Bruna J, LeCun Y, et al. Geometric deep learning: going beyond euclidean data[J]. IEEE Signal Processing Magazine, 2017, 34(4): 18-42.

[2] Ying Z, Bourgeois D, You J, et al. Gnnexplainer: Generating explanations for graph neural networks[C]//Advances in neural information processing systems. 2019: 9244-9255.

[3] Ying R, He R, Chen K, et al. Graph convolutional neural networks for web-scale recommender systems[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2018: 974-983.

[4] Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.

[5] Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[J]. arXiv preprint arXiv:1710.10903, 2017.

[6] Xu K, Hu W, Leskovec J, et al. How powerful are graph neural networks?[J]. arXiv preprint arXiv:1810.00826, 2018.

[7] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.

[8] Huang G, Liu Z, Van Der Maaten L, et al. Densely connected convolutional networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4700-4708.

[9] Li Q, Han Z, Wu X M. Deeper insights into graph convolutional networks for semi-supervised learning[J]. arXiv preprint arXiv:1801.07606, 2018.

[10] Zhao L, Akoglu L. Pairnorm: Tackling oversmoothing in gnns[J]. arXiv preprint arXiv:1909.12223, 2019.

[11] Xu K, Li C, Tian Y, et al. Representation learning on graphs with jumping knowledge networks[J]. arXiv preprint arXiv:1806.03536, 2018.

[12] Li G, Muller M, Thabet A, et al. Deepgcns: Can gcns go as deep as cnns?[C]//Proceedings of the IEEE International Conference on Computer Vision. 2019: 9267-9276.

[13] Yu F, Koltun V. Multi-scale context aggregation by dilated convolutions[J]. arXiv preprint arXiv:1511.07122, 2015.

[14] Rong Y, Huang W, Xu T, et al. Dropedge: Towards deep graph convolutional networks on node classification[C]//International Conference on Learning Representations. 2019.

[15] Zhou K, Dong Y, Lee W S, et al. Effective training strategies for deep graph neural networks[J]. arXiv preprint arXiv:2006.07107, 2020.

[16] Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[J]. arXiv preprint arXiv:1502.03167, 2015.

[17] Wu F, Zhang T, Souza Jr A H, et al. Simplifying graph convolutional networks[J]. arXiv preprint arXiv:1902.07153, 2019.

[18] http://web.stanford.edu/class/cs224w/

[19] https://www.wikiwand.com/zh/%E5%8D%A1%E6%8B%89%E6%AF%94%E2%80%93%E4%B8%98%E6%B5%81%E5%BD%A2

[20] https://mp.weixin.qq.com/s/1RUdmTr4bHjm6XYVdVRv5A

作者简介：贺华瑞，2020年毕业于西安电子科技大学，获得工学学士学位。现于中国科学技术大学电子工程与信息科学系的 MIRA Lab 实验室攻读研究生，师从王杰教授。研究兴趣包括知识表示与知识推理。

下载一：中文版！学习TensorFlow、PyTorch、机器学习、深度学习和数据结构五件套！

后台回复【五件套】
下载二：南大模式识别PPT

后台回复【南大模式识别】

说个正事哈

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面最上方“深度学习自然语言处理”，进入公众号主页。

（2）点击右上角的小点点，在弹出页面点击“设为星标”，就可以啦。

感谢支持，比心。

投稿或交流学习，备注：昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多：机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦

推荐两个专辑给大家：

专辑 | 李宏毅人类语言处理2020笔记

专辑 | NLP论文解读

专辑 | 情感分析

整理不易，还望给个在看！