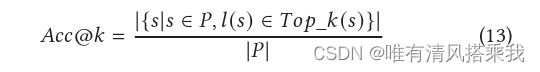POI推荐文献阅读笔记3：Predicting Human Mobility via Graph Convolutional Dual-attentive Networks
POI推荐文献阅读笔记3： Predicting Human Mobility via Graph Convolutional Dual-attentive Networks
- 1.摘要
- 2.贡献
- 3.模型分析
-
- 3.1问题公式化
- 3.2模块详情
-
- 3.2.1时空嵌入模块
-
- 时间戳嵌入
- 位置嵌入
- 全局嵌入
- 轨迹位置编码
- 3.2.2轨迹编码器--解码器模块
-
- 编码器
- 解码器
- 目标函数
- 3.2.3模型训练和优化
-
- 训练阶段的三个训练技巧
- 3.3 模型整体流程
- 4.实验
-
-
- 4.1数据集及评价指标
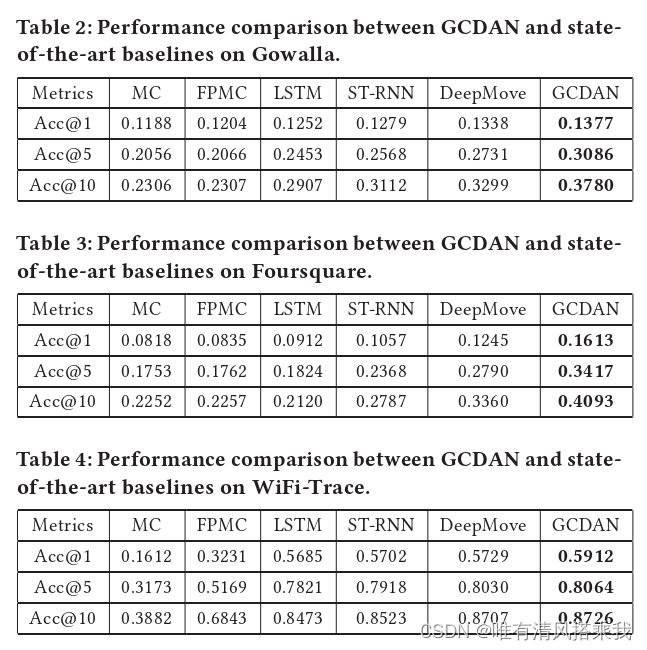
- 4.2结果对比
-
1.摘要
人类移动性预测对于智能交通和个性化推荐系统等各种应用具有重要意义。尽管许多传统的基于模式的方法和基于深度模型的(比如循环神经网络)方法已经被开发出来用于该任务，但它们本质上并不能很好地处理轨迹数据的稀疏性和不准确性以及序列依赖的复杂高阶性质，而这些都是移动性预测中的典型挑战。针对上述问题，本文提出了一种新颖的图卷积双注意力网络( Graph Convolutional Dual-attentive Networks，GCDAN )框架，该框架由时空嵌入和轨迹编解码两个模块组成。第一个模块使用双向扩散图卷积来保持位置嵌入中的空间依赖性。第二个模块使用了基于序列到序列架构的双注意力机制，以有效地提取轨迹内的长序列依赖关系和不同轨迹之间的相关性，从而进行预测。在三个真实数据集上的大量实验表明，与最先进的baseline相比，GCDAN获得了显著的性能增益。
2.贡献
1、据我们所知，我们是最早引入图卷积和双注意力机制来处理轨迹数据的稀疏性和不准确性以及人类移动预测问题中的高阶序列性的。
2、我们提出了一个新的移动性预测框架GCDAN，它由两个模块组成。第一个模块通过同时保留轨迹的空间依赖性和时间特性来学习轨迹位置的稠密表示。在此基础上，第二个模块进一步采用了序列到序列的架构，该架构充分考虑了复杂的序列依赖和用户偏好，在历史轨迹的指导下预测下一个位置
3、我们在三个真实的数据集(包括两个常用的数据集和一个新收集的数据集)上进行了广泛的实验，以评估所提出的框架的有效性。结果表明，GCDAN始终优于最先进的baseline。此外，我们公开发布了收集的数据集，作为移动预测问题的新基准，该数据集记录了一个最大的校园无线网络中的用户移动轨迹。
3.模型分析
3.1问题公式化
定义1(时空点)： L = { l 1 , . . . . . . ， l ∣ L ∣ } L = \lbrace l_1,......，l_{|L|}\rbrace L={l1,......，l∣L∣}定义为地点标识符的集合，那么对于一个时空点 p = ( l , t ) p=(l,t) p=(l,t)意思是一个用户到达在t时间到达l地点。
定义2(轨迹)： U = { u 1 , . . . . . . ， u ∣ U ∣ } U = \lbrace u_1,......，u_{|U|}\rbrace U={u1,......，u∣U∣}定义为用户的集合。对于一个用户u∈U其一个按时间排序的时空点序列 T u = p u 1 p u 2 p u 3 . . . p u m T_u=p^1_{u}p^2_{u}p^3_{u}...p^m_{u} Tu=pu1pu2pu3...pum, p u i p^i_{u} pui表示在轨迹 T u T_u Tu的第i个时空点。当然每个用户不同的轨迹的长度可能是不同的。
对于一个用户u∈U， S u = { T u 1 , T u 2 , T u 3 . . . T u ∣ S u ∣ } S_u=\lbrace T^1_{u}, T^2_{u},T^3_{u}...T^{|S_u|}_{u}\rbrace Su={Tu1,Tu2,Tu3...Tu∣Su∣}定义为其历史轨迹的集合，同时 T u ∼ = p u 1 p u 2 p u 3 . . . p u m {\overset{\thicksim}{{T}_{u}}}=p^1_{u}p^2_{u}p^3_{u}...p^m_{u} Tu∼=pu1pu2pu3...pum是其当前轨迹。基于此可以公式化地提出用户移动行为预测的问题：
对于任意的一个用户u，给定一个他的历史轨迹 S u S_u Su和当前轨迹 T u ∼ \overset{\thicksim}{{T}_{u}} Tu∼，目标是预测当前轨迹的下一个时空点比如 p u n + 1 p^{n+1}_u pun+1。
3.2模块详情
整个模型结构图如下：
3.2.1时空嵌入模块
时间戳嵌入
时间戳对齐到了一个固定的时间间隔内，时间间隔可以为一天或者一周。然后将固定时间间隔离散化为 ρ \rho ρ个时隙，对于每个时间戳进一步映射到相应的时隙，并将其以one-hot形式表示，维度为 ρ \rho ρ，叫做 v t v_t vt。
同时，使用了word2vec将 v t v_t vt转化为一个低维密集表示形式 h t h_t ht，方法是通过一个变换矩阵 Θ T ∈ R d 1 × ρ \Theta_T∈R^{d_1 ×\rho} ΘT∈Rd1×ρ，即 h t = Θ T v t h_t=\Theta_Tv_t ht=ΘTvt
位置嵌入
引入了图卷积来捕获空间依赖关系并减轻定位的不准确性。令 G = ( L , E , W ) G=(L,E,W) G=(L,E,W)其中L在之前已经定义过，E是边的集合，W是对于一个位置对子比如 ( l i , l j ) (l_i,l_j) (li,lj)计算其出现在历史轨迹中的次数。 w i j w_{ij} wij如果大于0表示这俩点之间有边，否则等于0.计算方式如下图：
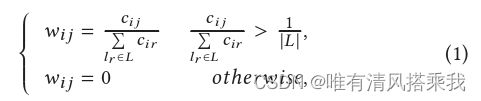
进一步将所有位置的one-hot表示形式定义为 V L V_L VL, H L = ( h l 1 , . . . , h l ∣ L ∣ ) H_L=(h_{l_1},...,h_{l_|L|}) HL=(hl1,...,hl∣L∣)是所有位置的稠密表示。
全局嵌入
对于一个时空点 p = ( l , t ) p=(l,t) p=(l,t)，全局嵌入 h p = h t ∣ ∣ h l h_p=h_t||hl hp=ht∣∣hl，||的意思是concatenate，所以 h p h_p hp的维度是 d 1 + d 2 d_1+d_2 d1+d2
轨迹位置编码
令 T = p 1 p 2 . . . p m T=p^1p^2...p^m T=p1p2...pm表示为一个轨迹，那么对T中的m个时空点进行全局嵌入后的形式则表示为 H T = h p 1 , . . . , h p m H_T=h_{p^1},...,h_{p^m} HT=hp1,...,hpm，进一步构建了一个新的位置向量 p o s i pos_i posi，维度为 d 1 + d 2 d_1+d_2 d1+d2，其计算方式如下：
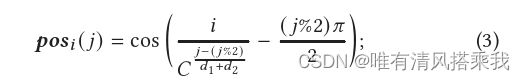
其中C是一个常数，决定位置编码的函数频率。最后对于T中的每一个时空点进行全局嵌入再加上这个新的位置向量就变成了 h p i = h p i + p o s i h_{p^i}=h_{p^i}+pos_i hpi=hpi+posi
3.2.2轨迹编码器–解码器模块
编码器
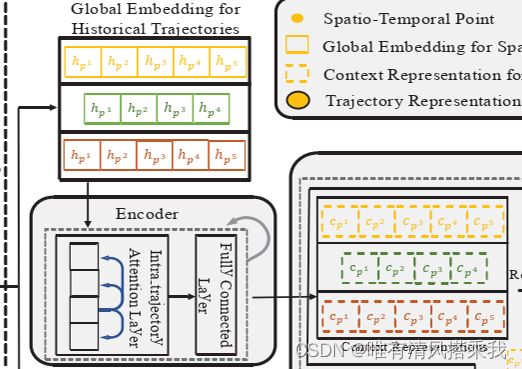
T = p 1 p 2 . . . p m T=p^1p^2...p^m T=p1p2...pm表示为一个轨迹，那么对T中的m个时空点进行全局嵌入后的形式则表示为 H T = h p 1 , . . . , h p m H_T=h_{p^1},...,h_{p^m} HT=hp1,...,hpm，然后进入编码器，即如上图所示。
轨迹中的顺序转移通常具有高阶性质，这意味着位置可能不依赖于相邻位置，而是依赖于轨迹序列中的一个较远的位置。因此，在编码器中设计了轨迹内注意力层，相比于RNN、LSTM等循环单元，能够更好地建模长距离依赖。
其计算过程是给定一个历史轨迹及其全局嵌入后的向量表示，对于每个时空点，intra-trajectory注意力层计算其和其他所有候选时空点之间的相似性，类似做softmax，但是对于两个时空点先经过一个函数f，这个f可以是点积也可是双线性函数等。最终得到每个时空点的上下文表示。计算方式如下图：
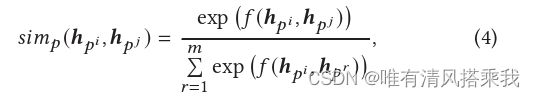
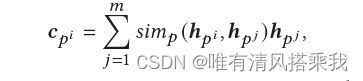至此历史轨迹部分进入解码器。
当前轨迹生成其全局嵌入表示后直接进入解码器部分。
解码器
分别看下历史轨迹和当前轨迹在解码器里的过程。
当前轨迹：其全局嵌入进来后也是经过intra-trajectory注意力层计算其和其他所有候选时空点之间的相似性，只不过这个操作只对轨迹T的最后一个时空点 p n p^n pn进行，从而产生 c p n ∼ \overset{\thicksim}{{c}_{p^n}} cpn∼。
同时对解码器过来的历史轨迹上下文表示进行了一个readout操作，其本质是对每一条历史轨迹的中的 c p j c_{p^j} cpj做了求和平均产生 x x x。原因是不同的历史轨迹可以显示不同的时空行为模式，当其作用在 c p n ∼ \overset{\thicksim}{{c}_{p^n}} cpn∼上可能产生不同的效果。
产生 x x x后，当前轨迹的 x x x表示形式为 x ∼ \overset{\thicksim}{{x}} x∼,进行类似softmax的操作。
最后的结果 v p n v_{p^n} vpn是对一条历史轨迹所有的 c p j c_{p^j} cpj与 c p n ∼ \overset{\thicksim}{{c}_{p^n}} cpn∼。做 s i m p ( ) sim_{p}() simp()× c p j c_{p^j} cpj求和后，乘上其与 x ∼ \overset{\thicksim}{{x}} x∼做的 s i m t ( ) sim_{t}() simt()结果。历史轨迹的条数为 ∣ S ∣ |S| ∣S∣，对每一条历史轨迹做同样的操作。对应的模型图部分和具体计算如下图所示。
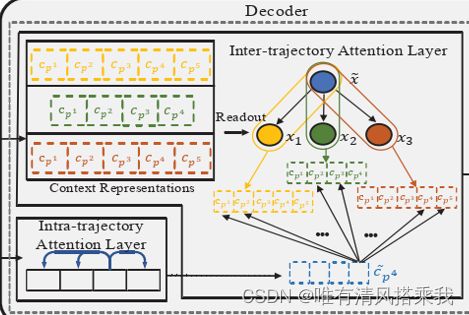
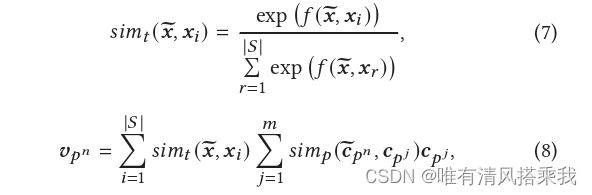
之后得到的 v p n v_{p^n} vpn再经过全连接层以及softmax输出最终的预测。
目标函数
总体上来说移动预测问题可以看作是一个多分类问题，因此最后将 v p n v_{p^n} vpn转化为 L L L中所有可能位置的概率分布。其计算方式如下：
训练模型使用的交叉熵损失函数如下：
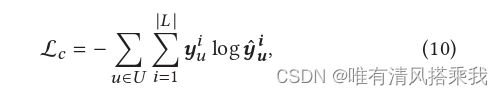
其中 y ^ u i {\hat{y}}_u^i y^ui代表用户u通过(9)得到的预测分布， y u i y_u^i yui代表用户u当前轨迹中下一个位置的one-hot真实值分布。为了避免过拟合将 L 2 L_2 L2正则化作用在所有参数上，最终的loss如下：
L是对所有参数正则化后的求和，α是一个平衡参数
3.2.3模型训练和优化
训练阶段的三个训练技巧
1、轨迹划分。
根据相邻两个时空点的时间间隔将用户的时空点序列划分为多个轨迹，这样可以带来两个好处。( 1 )划分方法使得可以使用上面提到的轨迹间注意力机制来捕获不同子序列对移动性预测的贡献。( 2 )令表示被划分的轨迹的个数。提高了计算效率
2、轨迹填充
被划分后的轨迹的长度不同，使得学习在所有历史轨迹中的时空点的上下文表示效率不高。为此设计了轨迹填充，通过填充虚拟时空点让所有的轨迹的长度等于最长的轨迹的长度。但是为了不影响注意力操作的结果，提出了mask向量 M \boldsymbol{M} M。具体来说，假设最长的轨迹的长度为 m ^ \hat{m} m^，一条轨迹的长度为 m m m，那么在 M \boldsymbol{M} M中，对应前 m m m个维度的mask向量为1，后 ( m ^ − m ) (\hat{m}-m) (m^−m)维度为0。基于此，可以重写公式(4)。
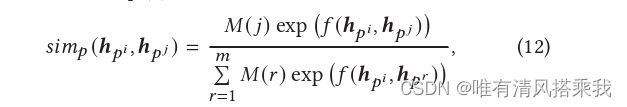
3、轨迹重用
为了进一步加强训练过程，我们可以重用当前待预测的轨迹来获得更多的监督信息。具体来说，假设当前轨迹为 T ∼ = p 1 . . p n \overset{\thicksim}{{T}}=p^1..p^n T∼=p1..pn，不仅预测其 p n + 1 p^{n+1} pn+1，希望生成另外的n-1个当前轨迹 T i ∼ = p 1 . . p i \overset{\thicksim}{{T}^{i}}=p^1..p^i Ti∼=p1..pi去预测 p i + 1 p^{i+1} pi+1。也就是说，对于当前轨迹 T ∼ = p 1 \overset{\thicksim}{{T}}=p^1 T∼=p1一直到 T ∼ = p 1 . . . p n \overset{\thicksim}{{T}}=p^1...p^n T∼=p1...pn，都去预测其下一个时空点。从同样，虽然全部的轨迹序列信息已经知道，但是不应该使用未来的信息，所以同样的也做了mask。
3.3 模型整体流程
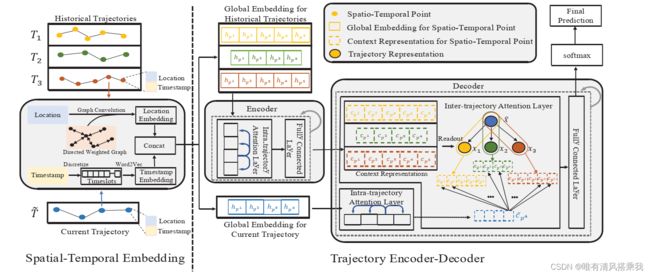
分为两部分，左边为时空嵌入部分，右边为轨迹编码器–解码器部分。
左边：历史轨迹时空点的位置经过图卷积后生成Location Embedding，同时时间戳经过时间间隔划分以及word2vec生成timestamp Embedding，两者做concat。
右边：历史轨迹中的每个时空点进行过全局嵌入后进入encoder，encoder由intra-trajectory attention layer 和全连接层组成，相当于一个小的单元，论文经过实验采用了3个单元，同时多头注意力的头数经过实验后设置为4。经过encoder后，历史轨迹生成其上下文表示，而具有全局嵌入的当前轨迹则经过intra-trajectory注意力层后只产生最后一个时空点的上下文表示。
之后，对历史轨迹的上下文表示经过readout操作后产生 x x x，与对应的当前轨迹的最后一个时空点的上下文表示的 x ∼ \overset{\thicksim}{{x}} x∼计算后，生成最后的 v p n v_{p^n} vpn， v p n v_{p^n} vpn在经过全连接层以及softmax后输出最终结果。同理，解码器之中的intra-trajectory attention layer与全连接层也相当于一个小的单元，其数目设置和头数设置与编码器相同。
4.实验
4.1数据集及评价指标
三个数据集，(1)Gowalla(2)Foursquare(3)WiFi-Trace。
评价指标：
4.2结果对比
