【KDD 2020】A Data-Driven Graph Generative Model for Temporal Interaction Networks

数据驱动的时间交互网络图生成模型

ABSTRACT

Deep graph generative models have recently received a surge of attention due to its superiority of modeling realistic graphs in a variety of domains, including biology, chemistry, and social science. Despite the initial success, most, if not all, of the existing works are designed for static networks. Nonetheless, many realistic networks are intrinsically dynamic and presented as a collection of system logs (i.e., timestamped interactions/edges between entities), which pose a newresearch direction for us: howcanwe synthesize realistic dynamic networks by directly learning from the system logs? In addition, how can we ensure the generated graphs preserve both the structural and temporal characteristics of the real data?

深层图生成模型由于其建模真实感图的优势，近年来在生物学、化学和社会科学等领域受到了极大的关注。尽管最初取得了成功，但现有的大部分(如果不是全部的话)工作都是为静态网络设计的。尽管如此，许多现实网络在本质上是动态的，并以系统日志的集合的形式呈现(即，实体之间带有时间戳的交互/边界)，这为我们提出了一个新的研究方向:我们如何通过直接从系统日志学习来合成现实的动态网络?此外，我们如何确保生成的图既保留了真实数据的结构特征又保留了时间特征?

To address these challenges, we propose an end-to-end deep generative framework named TagGen. In particular, we start with a novel sampling strategy for jointly extracting structural and temporal context information from temporal networks. On top of that, TagGen parameterizes a bi-level self-attention mechanism together with a family of local operations to generate temporal random walks. At last, a discriminator gradually selects generated temporal random walks, that are plausible in the input data, and feeds them to an assembling module for generating temporal networks. The experimental results in seven real-world data sets across a variety of metrics demonstrate that (1) TagGen outperforms all baselines in the temporal interaction network generation problem, and (2) TagGen significantly boosts the performance of the prediction models in the tasks of anomaly detection and link prediction.

为了应对这些挑战，我们提出了一个端到端的深层生成框架TagGen。特别是，我们从一种新的抽样策略开始，从时态网络中联合提取结构和时间上下文信息。在此基础上，TagGen参数化了一个双层自我注意机制和一系列局部操作来生成时间随机游动。最后，鉴别器逐渐地选择在输入数据中可信的生成的时间随机游动，并将其馈送给生成时序网络的组装模块。在七个真实数据集上的实验结果表明：（1）TagGen在时间交互网络生成问题上优于所有基线；（2）TagGen显著提高了预测模型在异常检测和链路预测任务中的性能。

INTRODUCTION

Graph presents a fundamental abstraction for modeling complex systems in a variety of domains, ranging from chemistry [39], security [4, 16, 42], recommendation [25, 33], and social science [34]. Therefore, mimicking and generating realistic graphs have been extensively studied in the past.

图为从化学[39]、安全[4,16,42]、推荐[25,33]和社会科学[34]等多个领域中建模复杂系统提供了基本抽象。因此，模拟和生成真实的图在过去得到了广泛的研究。

The traditional graph generative models are mostly designed to model a particular family of graphs based on some specific structural assumptions, such as heavy-tailed degree distribution [3], small diameter [10], local clustering [38], etc.

传统的图生成模型大多是基于某些特定的结构假设，如重尾度分布[3]、小直径[10]、局部聚类[38]等，对特定的图族进行建模。

In addition to the traditional graph generative models, a surge of research efforts on deep generative models [12, 17] have been recently observed in the task of graph generation. These approaches [5, 40] are trained directly from the input graphs without incorporating prior structural assumptions and often achieve promising performance in preserving diverse network properties of real networks.

除了传统的图形生成模型外，最近在图形生成任务中还观察到了对深层生成模型的研究热潮[12,17]。这些方法[5，40]是直接从输入图训练而来的，不需要加入预先的结构假设，并且通常在保持真实网络的不同网络特性方面取得了很好的性能。

Despite the initial success of deep generative models on graphs, most of the existing techniques are designed for static networks. Nonetheless, many real networks are intrinsically dynamic and stored as a collection of system logs (i.e., imestamped edges between entities). For example, in Fig. 1, an online transaction network can be intrinsically presented as a sequence of timestamped edges (i.e., financial transactions) between users. When an online transaction is completed, a system log file (i.e., a timestamped edge from one account to another) will be automatically generated and stored in the system. A conventional way of modeling such dynamic systems is to construct time-evolving graphs [36, 44] by aggregating timestamps into a sequence of snapshots. One drawback comes from the uncertainty of defining the proper resolution of the timeevolving graphs. If the resolution is too fine, the massive number of snapshots will bring intractable computational cost when training deep generative models; if the resolution is too coarse, fine-grained temporal context information (e.g., the addition/deletion of nodes and edges) might be lost during the time aggregation.

尽管图上的深层生成模型取得了初步成功，但现有的大多数技术都是为静态网络设计的。尽管如此，许多真实的网络本质上是动态的，并且存储为系统日志的集合（即实体之间的imestaped边缘）。例如，在图1中，在线交易网络本质上可以表示为用户之间的时间戳边缘（即，金融交易）的序列。当在线交易完成时，系统日志文件（即从一个帐户到另一个帐户的时间戳边缘）将自动生成并存储在系统中。对这种动态系统进行建模的传统方法是通过将时间戳聚合成一系列快照来构造时间演化图[36，44]。一个缺点来自于定义时间演化图的正确分辨率的不确定性。如果分辨率太细，在训练深层生成模型时，大量的快照将带来难以解决的计算开销；如果分辨率太粗，则在时间聚合过程中可能会丢失细粒度的时间上下文信息（如节点和边的添加/删除）。

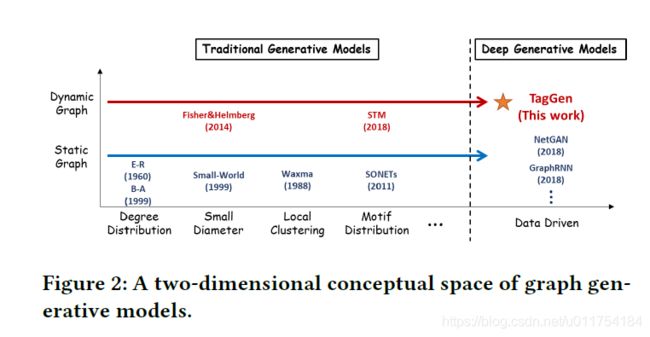
Fig. 2 compares various graph generators in a two-dimensional conceptual space in order to demonstrate the limitation of existing techniques as compared to ours. In this paper, for the first time, we aim to address the following three open challenges: (Q.1) Can we directly learn from the raw temporal networks (i.e., temporal interaction network) represented as a collection of timestamped edges (see Fig. 1 (b)) instead of constructing the time-evolving graphs? (Q.2) Can we develop an end-to-end deep generative model that can ensure the generated graphs preserve the structural and temporal characteristics (e.g., the heavy tail of degree distribution, and shrinking network diameter over time) of the original data?

图2比较了二维概念空间中的各种图形生成器，以证明与我们相比现有技术的局限性。在这篇论文中，我们第一次致力于解决以下三个开放性的挑战：（问题1）我们是否可以直接从表示为时间戳边集合（见图1（b））的原始时间网络（即时间交互网络）学习而不是构造时间演化图？（Q.2）我们是否可以开发一个端到端的深层生成模型，以确保生成的图保持原始数据的结构和时间特征（例如，度分布的重尾，随着时间的推移网络直径不断缩小）？

To this end, we propose TagGen, a deep graph generative model for temporal interaction networks to tackle all of the aforementioned challenges. We first propose a random walk sampling strategy to jointly extract the key structural and temporal context information from the input graphs. On top of that, we develop a bi-level self-attention mechanism which can be directly trained from the extracted temporal random walks while preserving temporal interaction network properties. Moreover, we designed a novel network context generation scheme, which defines a family of local operations to perform addition and deletion of nodes and edges, thus mimicking the evolution of real dynamic systems. In particular, TagGen maintains the state of the graph and generates new temporal edges by training from the extracted temporal random walks [27]; the addition operation randomly chooses a node to be connected with another one at a timestamp ; the deletion operation randomly terminates the interaction between two nodes at timestamp ; all the proposed operations are either accepted or rejected by a discriminator module in TagGen based on the current states of the constructed graph. At last, the selected plausible temporal random walks will be fed into an assembling module to generate temporal networks.

为此，我们提出了一个用于时态交互网络的深层图生成模型TagGen来解决上述所有挑战。首先提出一种随机游走抽样策略，从输入图中联合提取关键的结构和时间上下文信息。在此基础上，我们开发了一个双层次的自我注意机制，该机制可以直接从提取的时间随机游动中训练出来，同时保持时间交互网络的特性。此外，我们设计了一种新的网络上下文生成方案，该方案定义了一系列局部操作来执行节点和边的添加和删除，从而模拟了真实动态系统的演化。具体而言，TagGen通过训练提取的时间随机游动来保持图的状态并生成新的时间边[27]；加法运算在时间戳处随机选择一个节点与另一个节点连接；删除操作在时间戳处随机终止两个节点之间的交互；全部TagGen中的鉴别器模块根据所构造的图的当前状态来接受或拒绝所提出的操作。最后，将选择的似然时间随机游动输入到一个装配模块中，生成时序网络。

The main contributions of this paper are summarized below.
• Problem.We formally define the problem of temporal interaction network generation and identify its unique challenges arising from real applications.
• Algorithm. We propose an end-to-end learning framework for，temporal interaction network generation, which can (1) directly learn from a series of timestamped nodes and edges and (2) preserve the structural and temporal characteristics of the input data.
• Evaluations. We perform extensive experiments and case studies on seven real data sets, showing that TagGen achieves superior performances compared with the previous methods in the tasks of temporal graph generation and data augmentation.

PROBLEM DEFINITION

The main symbols used in this paper are summarized in Table 1 of Appendix A. We formalize the graph generation problem for
temporal interaction networks [21, 27, 29], and present our learning problem with inputs and outputs. Different from conventional dynamic graphs that are defined as a sequence of discrete snapshots, the temporal interaction network is represented as a collection of temporal edges. Each node is associated with multiple timestamped edges at different timestamps, which results in the different occurrences of node = {1 , . . . , }. For example, in Fig. 3, the node is associated with three occurrences {1 , 2 , 3 } that appear at timestamps 1, 2 and 3. The formal definitions of temporal occurrence and temporal interaction network are given as follows.

Definition 1 (Temporal Occurrence). In a temporal interaction network, a node is associated with a bag of temporal occurrences = {1 , 2 , . . .}, which instance the occurrences of node at timestamps {1, 2, . . .} in the network.

Definition 2 (Temporal Interaction Network). A temporal interaction network e = (e, e) is formed by a collection of nodes e = {1, 2, . . . , } and a series of timestamped edges e ={11 , 22 , ..., }, where = ( , ) .

Definition 3 (TemporalNetwork Neighborhood). Given a temporal occurrence at timestamp , the neighborhood of is
defined asN ( ) = { | ( , ) ≤ N , |− | ≤ N },where (·|·) denotes the shortest path between two nodes, N is theuser-defined neighborhood range, and N refers to the user-defined neighborhood time window.

Definition 4 (-Length TemporalWalk). Given a temporali nteraction network e, a -length temporal walk = {1, . . . , }
is defined as a sequence of incident temporal walks traversed one after another, i.e., = ( , ) , = 1, . . . , , where and are the source node and destination node of the th temporal walk in respectively.

Problem 1. Temporal Interaction Network Generation

Input: a temporal interaction network e, which is presented as a collection of timestamped edges {(1 , 1 )1 , . . . , (, ) }.

Output: a synthetic temporal interaction network e′ = (e ′, e′) that accurately captures the structural and temporal properties of the observed temporal network e.

MODEL

In this section, we introduce TagGen, a graph generative model for temporal interaction networks. The core idea of TagGen is to
train a bi-level self-attention mechanism together with a family of local operations to model and generate temporal random walks for assembling temporal interaction networks. In particular, we first introduce the overall learning framework of TagGen. Then, we discuss the technical details of TagGen regarding context sampling, sequence generation, sample discrimination, and graph assembling in temporal interaction networks. At last, we present an end-to-end optimization algorithm for training TagGen.

在这一节中，我们将介绍一个用于时态交互网络的图生成模型TagGen。TagGen的核心思想是训练一个双层的自我注意机制和一系列局部操作来建模和生成时间随机游动，以组装时间交互网络。特别是，我们首先介绍了TagGen的整体学习框架。然后，我们讨论了TagGen在时态交互网络中的上下文采样、序列生成、样本判别和图形组装等技术细节。最后，我们给出了塔根优化算法。

A Generic Learning Framework

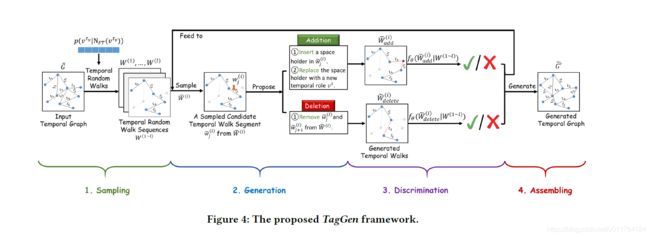
An overview of our proposed framework is presented in Fig. 4, which consists of four major stages. Given a temporal interaction network defined by a collection of temporal edges (i.e., timestamped interactions), we first extract network context information of temporal interaction networks by sampling a set of temporal random walks [27] via a novel sampling strategy. Second, we develop a deep generative mechanism, which defines a set of simple yet effective operations (i.e., addition and deletion over temporal edges) to generate synthetic random walks. Third, a discriminator is trained over the sampled temporal random walks to determine whether the generated temporal walks follow the same distributions as the real ones. At last, we generate temporal interactionnetwork, by collecting the qualified synthetic temporal walks via the discriminator. In the following subsections, we describe each stage of TagGen in details.

图4显示了我们提出的框架的概述，它包括四个主要阶段。给定一个由时间边缘集合（即时间戳交互）定义的时间交互网络，我们首先通过一种新的采样策略，通过采样一组时间随机游动来提取时间交互网络的网络上下文信息[27]。其次，我们开发了一个深层生成机制，它定义了一组简单而有效的操作（即在时间边缘上添加和删除）来生成合成随机游动。第三，在采样的时间随机游动上训练鉴别器，以确定生成的时间随机游动是否遵循与实际随机游动相同的分布。最后，通过鉴别器收集符合条件的合成时态行走，生成时态交互网络。在下面的小节中，我们将详细描述TagGen的每个阶段。