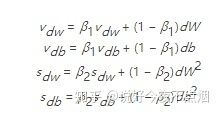Adam优化算法(Adam optimization algorithm)

Adam优化算法(Adam optimization algorithm)

Adam优化算法基本上就是将Momentum和RMSprop结合在一起。

1. 初始化

2.在第t次迭代中，用mini-batch梯度下降法计算出dw和db

3.计算Momentum指数加权平均数

4.用RMSprop进行更新

5.计算Momentum和RMSprop的修正偏差

6更新权重

 

其中Adam参数配置有:α 学习率/

β1 一阶矩估计的指数衰减率如0.9

β2 二阶矩估计的指数衰减率如0.999 该超参数在稀疏梯度（如在 NLP 或计算机视觉任务中）中应该设置为接近 1 的数。

 是非常小参数，防止在实现中除以0 分母防止为0 如 10E-8

 

Adam优势：

是一种在深度学习模型中用来代替随机梯度下降的优化算法

结合了AdaGrad和RMSProp算法最优性能 调参相对简单 默认参数就可处理大部分的问题。

 

Momentum介绍：

通常情况下我们把数据集拆解为一小批一小批进行训练，就是我们常用的Mini-batch SGD算法，虽然能带来很好的训练速度但是在达到最优点的时候并不是总是能够到达真正的全局最优点，而是在最优点附近不断地徘徊，另一个缺点就是需人工去选择一个合适的learningLate，大了会过拟合，小了会导致收敛速度过慢。于是我们所希望的仅仅是网络在优化的时候网络的损失函数有一个很好的收敛速度同时又不至于摆动幅度太大。

Momentum基于梯度的移动指数加权平均，假设在当前的迭代步骤第 tt 步中，那么基于Momentum优化算法可以写成下面的公式：

vdw=βvdw+(1−β)dWvdw=βvdw+(1−β)dW (1)

vdb=βvdb+(1−β)dbvdb=βvdb+(1−β)db (2)

W=W−αvdwW=W−αvdw (3)

b=b−αvdbb=b−αvdb (4)

主要思想是对网络中的参数进行平滑处理，让梯度摆动的幅度变小。

在上面的公式中vdwvdw和vdbvdb分别是损失函数在前t−1t−1轮迭代过程中累积的梯度梯度动量，ββ是梯度累积的一个指数，这里我们一般设置值为0.9。所以Momentum优化器的主要思想就是利用了类似与移动指数加权平均的方法来对网络的参数进行平滑处理的，让梯度的摆动幅度变得更小。

dWdW和dbdb分别是损失函数反向传播时候所求得的梯度，下面两个公式是网络权重向量和偏置向量的更新公式，αα是网络的学习率。当我们使用Momentum优化算法的时候，可以解决mini-batch SGD优化算法更新幅度摆动大的问题，同时可以使得网络的收敛速度更快

RMSProp：

在上面的Momentum优化算法中，虽然初步解决了优化中摆动幅度大的问题。所谓的摆动幅度就是在优化中经过更新之后参数的变化范围，如下图所示，蓝色的为Momentum优化算法所走的路线，绿色的为RMSProp优化算法所走的路线。

为了进一步优化损失函数在更新中存在摆动幅度过大的问题，并且进一步加快函数的收敛速度，RMSProp算法对权重WW和偏置bb的梯度使用了微分平方加权平均数。

其中，假设在第tt轮迭代过程中，各个公式如下所示：

所不同的是，RMSProp算法对梯度计算了微分平方加权平均数。这种做法有利于消除了摆动幅度大的方向，用来修正摆动幅度，使得各个维度的摆动幅度都较小。另一方面也使得网络函数收敛更快。（比如当 dWdW 或者 dbdb 中有一个值比较大的时候，那么我们在更新权重或者偏置的时候除以它之前累积的梯度的平方根，这样就可以使得更新幅度变小）。为了防止分母为零，使用了一个很小的数值 ϵϵ 来进行平滑，一般取值为10−810−8。

 

Adam：

有了上面两种优化算法，一种可以使用类似于物理中的动量来累积梯度，另一种可以使得收敛速度更快同时使得波动的幅度更小。那么讲两种算法结合起来所取得的表现一定会更好。Adam（Adaptive Moment Estimation）算法是将Momentum算法和RMSProp算法结合起来使用的一种算法，我们所使用的参数基本和上面讲的一致，在训练的最开始我们需要初始化梯度的累积量和平方累积量。

vdw=0,vdb=0;sdw=0,sdb=0

假设在训练的第tt轮训练中，我们首先可以计算得到Momentum和RMSProp的参数更新：

由于移动指数平均在迭代开始的初期会导致和开始的值有较大的差异，所以我们需要对上面求得的几个值做偏差修正

通过上面的公式，我们就可以求得在第tt轮迭代过程中，参数梯度累积量的修正值，从而接下来就可以根据Momentum和RMSProp算法的结合来对权重和偏置进行更新。

上面的所有步骤就是Momentum算法和RMSProp算法结合起来从而形成Adam算法。在Adam算法中，参数 β1β1 所对应的就是Momentum算法中的 ββ 值，一般取0.9，参数 β2β2 所对应的就是RMSProp算法中的 ββ 值，一般我们取0.999，而 ϵϵ 是一个平滑项，我们一般取值为 10−810−8，而学习率 αα 则需要我们在训练的时候进行微调。

 

原文链接：深度学习优化算法解析(Momentum, RMSProp, Adam)

 

偏差修正：

由指数加权平均来看出，每个最新的数据值，依赖于以前的数据结果。

一般令第一个数值为0，即v0=0；但此时初期的几个计算结果就会与真实的平均值有较大偏差，具体如下：

有了指数加权平均、偏差修正的基础，就可以研究一下深度学习中优化算法的实现原理了。

深度学习--优化器算法Optimizer详解（BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam） - 郭耀华 - 博客园

 

L0,L1,L2范数

即相对应的lasso 和岭回归，