量子+AI应用：量子计算与神经网络

量子+AI应用：量子计算与神经网络

文章主题：

神经网络是当下计算应用中发展最快，使用最广的机器学习算法。然而，由于传统的神经网络只能使用单个网络来存储许多算法模式，随着应用不断复杂化导致网络结构不断扩大，存储性能瓶颈已逐渐凸显。

而量子神经网络是根据量子计算机的特性设计的神经网络。研究者们根据量子计算机所提供的基本计算单元（即量子逻辑门）进行量子线路设计，以实现神经网络的计算。通过在量子计算机或量子器件的基础上构造神经网络，利用量子计算超高速、超并行、指数级容量的特点，来改进神经网络的结构和性能，可以使用许多网络来存储许多算法模式。

1.神经网络

1.1 什么是神经网络

神经网络，也称为人工神经网络 (ANN) ，是机器学习的子集，并且是深度学习算法的核心。其名称和结构是受人类大脑的启发，模仿了生物神经元信号相互传递的方式，以数学和物理方法及从信息处理的角度对人脑生物神经网络进行抽象并建立起来的某种简化模型。

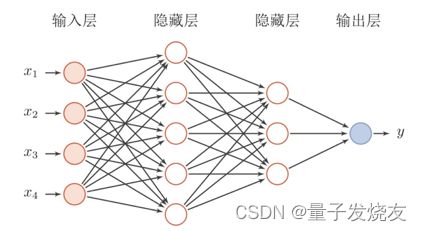
人工神经网络 (ANN) 由节点层组成，包含一个输入层、一个或多个隐藏层和一个输出层。 每个节点也称为一个人工神经元，人工神经元是神经网络的基本元素，它们连接到另一个节点，具有相关的权重和阈值。如果任何单个节点的输出高于指定的阈值，那么该节点将被激活，并将数据发送到网络的下一层。否则，不会将数据传递到网络的下一层。下图是一个人工神经网络的构造图，每一个圆代表着一个神经元，他们连接起来构成了一个网络。

神经网络反映人类大脑的行为，允许计算机程序识别模式，以及解决人工智能、机器学习和深度学习领域的常见问题。其依赖于训练数据随时间的推移不断学习并提高其准确性。 然而，一旦这些学习算法的准确性经过调优，它们便是计算科学和人工智能中的强大工具，我们可以快速地对数据进行分类。与由人类专家进行的人工识别相比，语音识别或图像识别任务可能仅需要几分钟而不是数小时。最著名的神经网络之一是 Google 的搜索算法。

1.2 人工神经元

人工神经元的工作原理，如下图所示

上面的x是神经元的输入，相当于树突接收的多个外部刺激。w是每个输入对应的权重，代表了每个特征的重要程度，它对应于每个输入特征，影响着每个输入x的刺激强度。假设只有3个特征，那么x就可以用（x1，x2，x3）。b表示阈值，用来影响预测结果。z就是预测结果。

所以有：$‘z=(x_1\ast w_1+x_2\ast w_2+x_3\ast w_3)-b‘$

上面这个式子在业内我们称之为逻辑回归。在实际的神经网络中，我们不能直接用逻辑回归，必须要在逻辑回归外面再套上一个函数，这个函数我们就称它为激活函数。

如在1943年，McCulloch和Pitts将上图的神经元结构用一种简单的模型进行了表示，构成了一种人工神经元模型，也就是现在经常用到的“M-P神经元模型”，如下图所示：

从上图M-P神经元模型可以看出，神经元的输出为

$‘y=f({\sum }_{i=1}^n{w}_i{x}_i-\theta )‘$

其中θ为神经元的激活阈值，函数f(⋅)也被称为是激活函数。

1.3 神经网络的类型

1.3.1 感知器

感知器是最古老的神经网络，由 Frank Rosenblatt 于 1958 年创建。它有一个神经元，是神经网络最简单的形式：

上图中，x是神经元的输入，代表着输入特征向量， Output是预测结果。

1.3.2 前馈神经网络（FNN）

前馈神经网络（Feedforward Neural Network，FNN）是最早发明的简单人工神经网络，由输入层、一个或多个隐藏层以及输出层组成。在前馈神经网络中，各神经元分别属于不同的层。每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层叫输入层，最后一层叫输出层，其它中间层叫做隐藏层。整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示。

1.3.3 卷积神经网络 (CNN)

卷积神经网络（CNN）是一类包含卷积计算且具有深度结构的前馈神经网络，是深度学习的代表算法之一。卷积神经网络具有表征学习能力，能够按其阶层结构对输入信息进行平移不变分类，通常用于图像识别、模式识别和/或计算机视觉。这些网络利用线性代数的原理（特别是矩阵乘法）来识别图像中的模式。卷积神经网络的构成分为：输入层、卷积层、池化层和全连接层，其结构如下图所示。

（1）输入层

整个网络的输入，一般代表了一张图片的像素矩阵。上图中最左侧三维矩阵代表一张输入的图片，三维矩阵的长、宽代表了图像的大小，而三维矩阵的深度代表了图像的色彩通道（channel）。

（2）卷积层

卷积层是卷积神经网络（CNN） 中最为重要的部分。卷积层中每一个节点的输入只是上一层神经网络中的一小块，一般来说，通过卷积层处理过的节点矩阵会变的更深。

（3）池化层

池化层不改变三维矩阵的深度，但是可以缩小矩阵的大小。池化操作可以认为是将一张分辨率高的图片转化为分辨率较低的图片。通过池化层，可以进一步缩小最后全连接层中节点的个数，从而到达减少整个神经网络参数的目的。池化层本身没有可以训练的参数。

（4）全连接层

卷积神经网络中的全连接层等价于传统前馈神经网络中的隐含层。全连接层位于卷积神经网络隐含层的最后部分，并只向其它全连接层传递信号。特征图在全连接层中会失去空间拓扑结构，被展开为向量并通过激励函数。

1.3.4 循环神经网络 (RNN)

循环神经网络 (RNN) 是一种使用顺序数据或时间序列数据的人工神经网络。这些深度学习算法通常用于顺序或时间问题，例如语言翻译、自然语言处理 (nlp)、语音识别和图像字幕；它们被整合到流行的应用程序中，例如 Siri、语音搜索和谷歌翻译。与前馈和卷积神经网络 (CNN) 一样，循环神经网络利用训练数据进行学习。

（循环神经网络（左侧）和前馈神经网络（右侧）的比较）

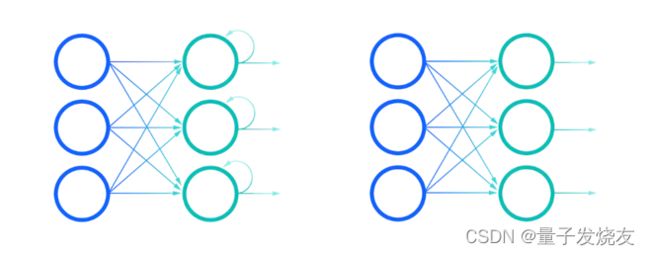
循环网络的另一个显着特征是它们在网络的每一层共享参数。虽然前馈网络在每个节点上具有不同的权重，但循环神经网络在网络的每一层内共享相同的权重参数。也就是说，这些权重仍然在通过反向传播和梯度下降的过程中进行调整，以促进强化学习。

1.4 神经网络与深度学习

训练深度神经网络的过程就叫做深度学习。网络构建好了后，我们只需要负责不停地将训练数据输入到神经网络中，它内部就会自己不停地发生变化不停地学习。打比方说我们想要训练一个深度神经网络来识别猫。我们只需要不停地将猫的图片输入到神经网络中去。训练成功后，我们任意拿来一张新的图片，它都能判断出里面是否有猫。

2 量子神经网络

量子神经网络（QNN）是前馈神经网络的一种，是基于量子力学原理的神经网络模型。通过将量子态的叠加思想引入到传统的前馈神经网络中，将神经网络的隐含层激励函数采用多个sigmoid函数进行叠加。一个sigmoid函数仅可以表示两个量级和状态，而线性叠加的sigmoid函数相邻之间有着不同的量子间隔。一个隐层的神经单元就能表示更多的量级和状态，这样通过对量子间隔的训练，训练样本输入数据的不确定性就能得到量化，不同数据将映射到不同的量级之上，利用多层的激励函数增加网络的模糊性，提高网络模式识别的准确性和确定性。

与经典神经网络相比，量子神经网络（QNN）具有以下几个优点：（1）更快的计算速度；（2）更高的记忆容量；（3）更小的网络规模；（4）可消除灾变性失忆现象。因此其十分适合于未来数据海量、计算要求高的任务。

2.1 量子神经网络的工作原理

人工神经网络 (ANN)的许多功能源于其并行分布式信息处理能力和神经元变换的非线性。然而，量子理论的态叠加原理使 QNN具有比ANN更强的并行处理能力并能处理更大型数据集。根据量子计算原理，一个n位量子寄存器可以同时保存 2^n个n位二进制数 (0到 2^n一1)，它们各以一定的概率存在。量子计算系统以这种方式指数地增加存储能力并能并行处理一个 n位量子寄存器的所有 2^n个数，它的一次运算可产生 2^n个运算结果，相当于常规计算 2^n次操作。但在读出量子计算的输出结果即测量量子寄存器的态时，其叠加态将坍缩 (或消相干)到其中之一个基态上，因而测量时只能测得一个结果。例如在量子神经元模型中，感知器的权矢被一个波函数0(w, t)所取代，0(W, t)是所有可能的经典权矢的量子相干叠加，当叠加权矢与环境作用时(如受到实际输入的激励)，它必定会消相干到其中之一的基态上，即坍缩到经典权矢上。

接下来我们将尝试构建一个量子神经网络，以下是量子神经网络的工作原理。

首先向网络提供一些数据x，构建输入量子态：

$‘x\to |\psi (x)⟩‘$

将一个二维向量x变换成一个角。

$‘f(x)=2{\cos }^{-1}(\sqrt{\frac{x_0^2}{x_0^2+x_1^2}})‘$

当x被编码为量子态，我们应用一系列量子门。

$‘U_n({\theta }_n)U_{n-1}({\theta }_{n-1})...U_2({\theta }_2)U_1({\theta }_1)|\psi (x)⟩‘$

网络的输出设为π(x，0)。是最后一个量子比特被测量为 |1〉状态的概率（Z_n-1代表将Z门应用到最后的量子比特），加上一个经典的偏置项。

$‘\pi (x,\theta )=\frac{1}{2}(1+|\psi (x)⟩U(\theta {)}^{†}{Z}_{n-1}U(\theta )|\psi (x)⟩)+b‘$

最后，在输出的数据中取出和 x 有关联的标签，用来计算样本上的损失——我们将使用二次损失，如下：

$‘C(X,\theta )={\sum }_{x\in X}^{}l(x,\theta )‘$

从输出的数据中可以得到网络 p 的预测：

$`p=\left{\begin{matrix}

0 & \pi (x,\theta )<0.5 \

1 &\pi (x,\theta )\ge 0.5

\end{matrix}\right.`$

计算损失函数的梯度。

$‘l(x,\theta )‘$

2.2 如何在量子计算机上计算梯度

先求损失函数对θ_i的微分：

$‘{\partial }_{{\theta }_i}l(x,\theta )=(\pi (x,\theta )-y(x)){\partial }_{{\theta }_i}\pi (x,\theta )‘$

展开最后一项：

$‘{\partial }_{{\theta }_i}\pi (x,\theta )={\partial }_{{\theta }_i}(\frac{1}{2}(1+|\psi (x)⟩)U(\theta {)}^{†}{Z}_{n-1}U(\theta )|\psi (x)⟩+b)‘$

通过求导可以去掉常数项。

$‘\frac{1}{2}{\partial }_{{\theta }_i}⟨\psi (x)|U(\theta {)}^{†}{Z}_{n-1}U(\theta )|\psi (x)⟩‘$

使用乘积法则进一步展开：

$`\frac{1}{2}(\left \langle \psi (x)\right |(\partial_{\theta {i} }U(\theta ) )^{\dagger } Z{n-1} U(\theta )\left | \psi (x) \right \rangle

• \left \langle \psi (x)\right |(U(\theta ) )^{\dagger } Z_{n-1} \partial _{\theta _{i} } U(\theta )\left | \psi (x) \right \rangle)`$

通过 Hermitian 共轭，可以转化为下面这个简单的公式：

$‘Re(⟨\psi (x)|({\partial }_{{\theta }_i}U(\theta ){)}^{†}{Z}_{n-1}U(\theta )|\psi (x)⟩‘$

U(θ) 由多个门组成，每一个门又由不同的参数控制，求U的偏导数只需要求门$‘U_i({\theta }_i)‘$对$‘{\theta }_i‘$的偏导数：

$‘{\partial }_{{\theta }_i}U(\theta )=U_n({\theta }_n)U_{n-1}({\theta }_{n-1})...{\partial }_{{\theta }_i}{U}_i({\theta }_i...U_2({\theta }_2)U_1({\theta }_1))‘$

我们把$‘U_i‘$定义为相同的形式，称为G门，当然形式不是唯一的。

$`G(\theta )=\begin{bmatrix}

\cos \theta &\sin \theta \

-\sin \theta&\cos \theta

\end{bmatrix}`$

定义了$‘U_i‘$的形式后，就能找到它的导数：

$`\delta _{\theta } G(\theta )=\begin{bmatrix}

-\sin \theta &\cos \theta \

-\cos \theta &-\sin \theta

\end{bmatrix}`$

可以用G门来表示导数：

$‘{\delta }_{\theta }G(\theta )=G(\theta +\frac{\pi }{2})‘$

构造出一个电路来得到所需的内积形式：

$‘Re(⟨\psi |A{Z}_{n-1}B|\psi ⟩)‘$

Hadamard测试是最简单的方法——首先，准备好输入的量子态，并将辅助态制备为叠加态：

$‘\frac{1}{\sqrt{2}}(|0⟩+|1⟩)|\psi ⟩‘$

现在对|ψ>应用Z_n-1B，约束辅助态是|1>：

$‘\frac{1}{\sqrt{2}}(|0⟩|\psi ⟩+|1⟩Z_{n-1}B|\psi ⟩‘$

然后翻转辅助态，用A做同样的操作：

$‘\frac{1}{\sqrt{2}}(|0⟩A|\psi ⟩+|1⟩Z_{n-1}B|\psi ⟩‘$

最后，对辅助态使用另一个Hadamard门：

$‘\frac{1}{\sqrt{2}}(|0⟩(A+Z_{n-1}B)|\psi ⟩+|1⟩(A-Z_{n-1}B)|\psi ⟩‘$

现在辅助态等于0的概率是：

$‘p(0)=\frac{1}{2}+\frac{1}{2}Re(⟨\psi |A{Z}_{n-1}B|\psi ⟩‘$

因此如果我们用U(θ)代替B，用U(θ)的共轭对$‘{\theta }_i‘$的导数来代替A，然后辅助量子比特为0的概率将会给我们π(x，θ)对$‘{\theta }_i‘$的梯度。

2.3 建立量子神经网络

导入所有需要启动的模块：

from qiskit import QuantumRegister, ClassicalRegister

from qiskit import Aer, execute, QuantumCircuit

from qiskit.extensions import UnitaryGate

import numpy as np

将功能(前四列)与标签分开：

data = np.genfromtxt("processedIRISData.csv", delimiter=",")

X = data[:, 0:4]

features = np.array([convertDataToAngles(i) for i in X])

Y = data[:, -1]

构建一个为我们进行功能映射的函数。由于输入向量是归一化的和4维的，因此映射有一个超级简单的选择-使用2个量子位来保存编码数据，并使用仅将输入向量重新创建为量子态的映射。为此，我们需要两个函数-一个从向量中提取角度：

def convertDataToAngles(data):

"""

Takes in a normalised 4 dimensional vector and returns

three angles such that the encodeData function returns

a quantum state with the same amplitudes as the

vector passed in.

"""

prob1 = data[2] ** 2 + data[3] ** 2

prob0 = 1 - prob1

angle1 = 2 * np.arcsin(np.sqrt(prob1))

prob1 = data[3] ** 2 / prob1

angle2 = 2 * np.arcsin(np.sqrt(prob1))

prob1 = data[1] ** 2 / prob0

angle3 = 2 * np.arcsin(np.sqrt(prob1))

return np.array([angle1, angle2, angle3])

另一种将角度转换为量子态的方法：

def encodeData(qc, qreg, angles):

"""

Given a quantum register belonging to a quantum

circuit, performs a series of rotations and controlled

rotations characterized by the angles parameter.

"""

qc.ry(angles[0], qreg[1])

qc.cry(angles[1], qreg[1], qreg[0])

qc.x(qreg[1])

qc.cry(angles[2], qreg[1], qreg[0])

qc.x(qreg[1])

编写实现U (θ)所需的函数，该函数将采用RY和CX交替层的形式。从G门开始：

def GGate(qc, qreg, params):

"""

Given a parameter α, return a single

qubit gate of the form

[cos(α), sin(α)]

[-sin(α), cos(α)]

"""

u00 = np.cos(params[0])

u01 = np.sin(params[0])

gateLabel = "G({})".format(

params[0]

)

GGate = UnitaryGate(np.array(

[[u00, u01], [-u01, u00]]

), label=gateLabel)

return GGate

def GLayer(qc, qreg, params):

"""

Applies a layer of GGates onto the qubits of register

qreg in circuit qc, parametrized by angles params.

"""

for i in range(2):

qc.append(GGate(qc, qreg, params[i]), [qreg[i]])

接下来进行CX门操作：

def CXLayer(qc, qreg, order):

"""

Applies a layer of CX gates onto the qubits of register

qreg in circuit qc, with the order of application

determined by the value of the order parameter.

"""

if order:

qc.cx(qreg[0], qreg[1])

else:

qc.cx(qreg[1], qreg[0])

将它们放在一起以获得U (θ)：

def generateU(qc, qreg, params):

"""

Applies the unitary U(θ) to qreg by composing multiple

G layers and CX layers. The unitary is parametrized by

the array passed into params.

"""

for i in range(params.shape[0]):

GLayer(qc, qreg, params[i])

CXLayer(qc, qreg, i % 2)

接下来创建一个函数获取网络的输出，而另一个函数会将这些输出转换为类预测：

def getPrediction(qc, qreg, creg, backend):

"""

Returns the probability of measuring the last qubit

in register qreg as in the |1⟩ state.

"""

qc.measure(qreg[0], creg[0])

job = execute(qc, backend=backend, shots=10000)

results = job.result().get_counts()

if '1' in results.keys():

return results['1'] / 100000

else:

return 0

def convertToClass(predictions):

"""

Given a set of network outputs, returns class predictions

by thresholding them.

"""

return (predictions >= 0.5) * 1

构建一个在网络上执行前向传递的功能-向其提供一些数据，对其进行处理，并提供网络输出：

def forwardPass(params, bias, angles, backend):

"""

Given a parameter set params, input data in the form

of angles, a bias, and a backend, performs a full

forward pass on the network and returns the network

output.

"""

qreg = QuantumRegister(2)

anc = QuantumRegister(1)

creg = ClassicalRegister(1)

qc = QuantumCircuit(qreg, anc, creg)

encodeData(qc, qreg, angles)

generateU(qc, qreg, params)

pred = getPrediction(qc, qreg, creg, backend) + bias

return pred

编写测量梯度所需的所有功能，需要能够应用U (θ)的受控版本：

def CGLayer(qc, qreg, anc, params):

"""

Applies a controlled layer of GGates, all conditioned

on the first qubit of the anc register.

"""

for i in range(2):

qc.append(GGate(

qc, qreg, params[i]

).control(1), [anc[0], qreg[i]])

def CCXLayer(qc, qreg, anc, order):

"""

Applies a layer of Toffoli gates with the first

control qubit always being the first qubit of the anc

register, and the second depending on the value

passed into the order parameter.

"""

if order:

qc.ccx(anc[0], qreg[0], qreg[1])

else:

qc.ccx(anc[0], qreg[1], qreg[0])

def generateCU(qc, qreg, anc, params):

"""

Applies a controlled version of the unitary U(θ),

conditioned on the first qubit of register anc.

"""

for i in range(params.shape[0]):

CGLayer(qc, qreg, anc, params[i])

CCXLayer(qc, qreg, anc, i % 2)

创建一个计算期望值的函数：

def computeRealExpectation(params1, params2, angles, backend):

"""

Computes the real part of the inner product of the

quantum states produced by acting with U(θ)

characterised by two sets of parameters, params1 and

params2.

"""

qreg = QuantumRegister(2)

anc = QuantumRegister(1)

creg = ClassicalRegister(1)

qc = QuantumCircuit(qreg, anc, creg)

encodeData(qc, qreg, angles)

qc.h(anc[0])

generateCU(qc, qreg, anc, params1)

qc.cz(anc[0], qreg[0])

qc.x(anc[0])

generateCU(qc, qreg, anc, params2)

qc.x(anc[0])

qc.h(anc[0])

prob = getPrediction(qc, anc, creg, backend)

return 2 * (prob - 0.5)

计算出损失函数的梯度-最后做乘法解决梯度中的π ( x ，θ)-y( x )项：

def computeGradient(params, angles, label, bias, backend):

"""

Given network parameters params, a bias bias, input data

angles, and a backend, returns a gradient array holding

partials with respect to every parameter in the array

params.

"""

prob = forwardPass(params, bias, angles, backend)

gradients = np.zeros_like(params)

for i in range(params.shape[0]):

for j in range(params.shape[1]):

newParams = np.copy(params)

newParams[i, j, 0] += np.pi / 2

gradients[i, j, 0] = computeRealExpectation(

params, newParams, angles, backend

)

newParams[i, j, 0] -= np.pi / 2

biasGrad = (prob + bias - label)

return gradients * biasGrad, biasGrad

一旦有了梯度，就可以使用梯度下降以及称为动量的技巧来更新网络参数，这有助于加快训练时间：

def updateParams(params, prevParams, grads, learningRate, momentum):

"""

Updates the network parameters using gradient descent

and momentum.

"""

delta = params - prevParams

paramsNew = np.copy(params)

paramsNew = params - grads * learningRate + momentum * delta

return paramsNew, params

构建成本和准确性功能，了解网络如何响应培训：

def cost(labels, predictions):

"""

Returns the sum of quadratic losses over the set

(labels, predictions).

"""

loss = 0

for label, pred in zip(labels, predictions):

loss += (pred - label) ** 2

return loss / 2

def accuracy(labels, predictions):

"""

Returns the percentage of correct predictions in the

set (labels, predictions).

"""

acc = 0

for label, pred in zip(labels, predictions):

if label == pred:

acc += 1

return acc / labels.shape[0]

最后创建训练网络的函数，并调用它：

def trainNetwork(data, labels, backend):

"""

Train a quantum neural network on inputs data and

labels, using backend backend. Returns the parameters

learned.

"""

np.random.seed(1)

numSamples = labels.shape[0]

numTrain = int(numSamples * 0.75)

ordering = np.random.permutation(range(numSamples))

trainingData = data[ordering[:numTrain]]

validationData = data[ordering[numTrain:]]

trainingLabels = labels[ordering[:numTrain]]

validationLabels = labels[ordering[numTrain:]]

params = np.random.sample((5, 2, 1))

bias = 0.01

prevParams = np.copy(params)

prevBias = bias

batchSize = 5

momentum = 0.9

learningRate = 0.02

for iteration in range(15):

samplePos = iteration * batchSize

batchTrainingData = trainingData[samplePos:samplePos + 5]

batchLabels = trainingLabels[samplePos:samplePos + 5]

batchGrads = np.zeros_like(params)

batchBiasGrad = 0

for i in range(batchSize):

grads, biasGrad = computeGradient(

params, batchTrainingData[i], batchLabels[i], bias, backend

)

batchGrads += grads / batchSize

batchBiasGrad += biasGrad / batchSize

params, prevParams = updateParams(

params, prevParams, batchGrads, learningRate, momentum

)

temp = bias

bias += -learningRate * batchBiasGrad + momentum * (bias - prevBias)

prevBias = temp

trainingPreds = np.array([forwardPass(

params, bias, angles, backend

) for angles in trainingData])

print('Iteration {} | Loss: {}'.format(

iteration + 1, cost(trainingLabels, trainingPreds)

))

validationProbs = np.array(

[forwardPass(

params, bias, angles, backend

) for angles in validationData]

)

validationClasses = convertToClass(validationProbs)

validationAcc = accuracy(validationLabels, validationClasses)

print('Validation accuracy:', validationAcc)

return params

backend = Aer.get_backend('qasm_simulator')

learnedParams = trainNetwork(features, Y, backend)

参考链接：

1.https://zhuanlan.zhihu.com/p/215839390

2.https://www.ibm.com/cn-zh/cloud/learn/neural-networks#toc–bS0t361U

3.https://www.ibm.com/cn-zh/cloud/learn/neural-networks

4.https://max.book118.com/html/2019/0803/7024013124002044.shtm

5.https://towardsdatascience.com/quantum-machine-learning-learning-on-neural-networks-fdc03681aed3

6.https://cloud.tencent.com/developer/article/1781109

原文链接：

https://juejin.cn/post/7146139101098409998

https://mp.weixin.qq.com/s/D9gH50Fkm7bh9cHqbFTl7w