机器学习初探：（四）逻辑回归之二分类

（四）逻辑回归 - 二分类

​ 图片出处

在 机器学习初探：（一）机器学习绪论一文中，我们介绍了机器学习的基本类型。其中， 有监督学习问题又可分为两类：回归和分类。在前面的文章中，我们讨论了如何使用线性模型进行回归学习，包括预测餐厅利润额、预测房价。在这类问题中，我们根据训练集中的一系列特征，试着 推测出一系列连续值属性，比如利润、房价。那么，要做分类任务该怎么办？我们还可以使用线性回归来解决吗？

先来回顾一下什么是分类问题。它的目标是根据已知样本的某些特征，判断一个新的样本属于哪种已知的样本类。典型的分类问题包括：邮件是否为垃圾邮件、股票是涨还是跌、肿瘤是恶性还是良性等等。分类在计算机科学中具有广泛的应用，从医学图像分析到信用卡欺诈检测，包括语音识别，生物分类，手写体识别，地统计学和药物发现等。

回顾：分类和回归最大的区别在于，我们在试着推测出几个离散值（类别）属性。

我们以一个例子来说明，学生申请大学，学校需要对学生的学习成绩、综合素质等进行评估。评估结果为两种：未被录取（以 0 表示），被录取（以 1 表示）。假设一种简单的情况，Z 校所有申请者都需参加两门考试，根据这两门考试的成绩决定是否发放录取通知书。目前，Z 校收集了所有历史申请人的成绩以及录取结果的信息（如下表），试图构建一个分类模型，可以根据考试成绩预测某一申请人是否会被录取¹…

观测值 #	科目一成绩（$X_1$）	科目二成绩（$X_2$)	是否录取（$Y$）
1	34	78	0
2	30	43	0
3	35	72	0
4	60	86	1
…	…		…
100	74	89	1

逻辑回归（Logistic Regression）

为什么需要逻辑回归？

以上的例子是一个二分类任务，其输出标记有两种（即 0 和 1），而线性回归模型产生的预测值 $Z={\Theta }^{T}X$ 是实值，可能大于 1，也可能小于 0，显然无法直接用于分类问题。那么该怎么办呢？答案蕴涵在下式中：只需找到一个单调可微函数将线性回归模型的预测值映射到分类任务的真实标记 $y$ 上²。

有单调可微函数 $g(\cdot )$ ，令：
$$y=h_{\Theta }(x)=g({\Theta }^{T}X)$$
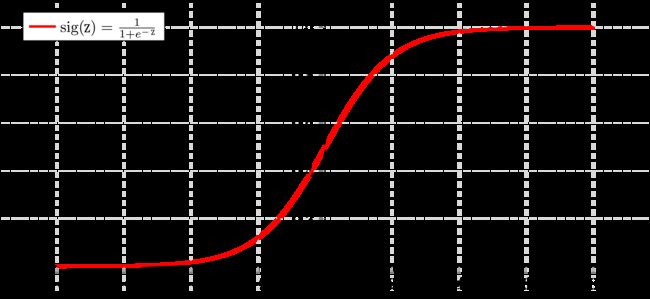
我们希望 $0\le h_{\Theta }(x)\le 1$，Sigmoid 函数即可以用作上式中的 $g(\cdot )$（Sigmoid 函数形式如图 1 所示），见下式：

图1 Sigmoid 函数

Sigmoid 函数将 $z$ 值转化为一个介于 0 和 1 之间的 $y$ 值，将Sigmoid函数作为 $g(\cdot )$ 代入 $h_{\Theta }(x)=g({\Theta }^{T}X)$ 中，得到：

$$h_{\Theta }(x)=\frac{1}{1+e^{-{\Theta }^{T}X}}$$

上式对应的模型称为“逻辑回归”（Logistic Regression）。

逻辑回归的预测值 $h_{\Theta }(x)$ 为介于 0 和 1之间的值，其可以理解为，在给定的输入 $x$ 的取值下，该例的标签 $y=1$ 的概率。 比如，在本节开篇的例子中，若模型预测值 $h_{\Theta }(x)=0.7$，其表示，基于该名学生的考试成绩，其被录取的概率为 70%。

假设，当 $h_{\Theta }(x)\ge 0.5$ （即，概率值大于50%） 时，预测 $y=1$；当 $h_{\Theta }(x)<0.5$ （即，概率值小于50%） 时，预测 $y=0$。对应到图1中，即：
$$y=\{\begin{array}{c}1,{\Theta }^{T}X\ge 0\\ 0,{\Theta }^{T}X<0\end{array}$$
其中，${\Theta }^{T}X=0$ 即为区分两个类别的决策边界（Decision Boundary）！

逻辑回归模型的基本形式：$h_{\Theta }(x)=\frac{1}{1+e^{-{\Theta }^{T}X}}$

因而，利用Logistic回归进行分类的主要思想是：根据现有数据对决策边界线建立回归公式，以此进行分类。特别需注意到，虽然它的名字是“回归”，但实际却是一种分类学习方法。这里的“回归”一词源于最佳拟合，表示要找出最佳拟合参数集³。

逻辑回归损失函数

先来回顾一下，我们用到的一些表达式：

• 训练集包括 $m$ 个训练样本：$\left\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots ,(x^{(m)},y^{(m)})\right\}$

• 每个训练样本：$x=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ ⋮\\ x_n\end{array}\right]\in {\mathbb{R}}^{n+1}$ ，其中 $x_0=1$, $y\in \left\{0,1\right\}$

• 模型假设：$\hat{y}=h_{\theta }(x)=\frac{1}{1+e^{-{\Theta }^{T}x}}$, 其中 $\hat{y}$ 表示 $y$ 的预测值

那么，如何找到最佳参数 $\Theta$ 呢？和线性回归问题一样，我们需要定义一个损失函数，来衡量每组参数下模型的预测准确度，从而选出预测效果最好的那组参数。先以只有一个样本的情况为例，逻辑回归的预测误差 Loss（$L$）定义为：
$$L(\hat{y},y)=-\left[ylog(\hat{y})+(1-y)log(1-\hat{y})\right]$$
这个式子代表什么呢？我们来分别看一下 $y=1$ （样本标签为1）和 $y=0$ （样本标签为0）两种情况：

如果 $y=1$： $L(\hat{y},y)=-log(\hat{y})$， 即预测值 $\hat{y}$ 趋近于0时，$L$ 趋近于无穷大，$\hat{y}$ 趋近于1时，$L$ 趋近于0。

如果 $y=0$： $L(\hat{y},y)=-log(1-\hat{y})$， 即预测值 $\hat{y}$ 趋近于1时，$L$ 趋近于无穷大，$\hat{y}$ 趋近于0时，$L$ 趋近于0。

对于一般的有 $m$ 个样本的情况，损失函数（Cost function）的形式如下：
$$\begin{array}{rl}J(\Theta )& =\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})\\ & =-\frac{1}{m}\sum _{i=1}^m[y^{(i)}log({\hat{y}}^{(i)})+(1-y^{(i)})log(1-{\hat{y}}^{(i)})]\end{array}$$

与线性回归问题一样，最优参数 $\Theta$ 可以使得损失函数 $J(\Theta )$ 最小化：
$$\underset{\Theta }{\min }J(\Theta )$$
求得上述最优参数取值之后，对于一个新的样本 $x$, 我们基于此求得 $h_{\Theta }(x)$ 值，用于预测新样本的类别（或属于某一类别的概率）：
$$h_{\Theta }(x)=\frac{1}{1+e^{-{\Theta }^{T}x}}$$

从计算图的角度理解梯度下降算法

和线性回归问题一样，逻辑回归也可通过梯度下降（Gradient Descent）算法来最小化 $J(\Theta )$。

梯度下降算法更新参数的一般形式为（同时更新所有参数 ${\theta }_j$）：
$${\theta }_j:={\theta }_j-\alpha \frac{\delta }{\delta {\theta }_j}J(\Theta )$$

什么是计算图（Computation Graph）

如何求得偏导数 $\frac{\delta }{\delta {\theta }_j}J(\Theta )$ 是梯度下降算法的关键。为了更好理解梯度下降算法，我们通过计算图来说明⁴。

计算图被定义为有向图，其中节点对应于数学运算。 计算图是表达和评估数学表达式的一种方式。

例如，对于有两个特征变量的逻辑回归，假设只有一个样本，即:
$$\begin{array}{rl}z& ={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2\\ \hat{y}& =h_{\theta }(x)=\sigma (z)\\ L(\hat{y},y)& =-ylog(\hat{y})-(1-y)log(1-\hat{y})\end{array}$$
其中，$\sigma (z)$ 代表sigmoid函数。

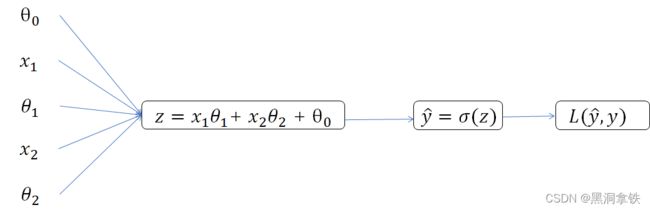
以上 $L(\hat{y},y)$ 的计算过程表示为计算图即为下图 2：

图2 通过计算图来理解预测误差的计算过程

接下来，按照相反的方向（即如下图 3 中红色箭头所示方向）来计算 $L(\hat{y},y)$ 关于 ${\theta }_i$ 的偏导数 $\delta {\theta }_i$。计算过程使用了复合函数求导的链式法则 （欲了解详情可参见链接：复合函数求导链式法则⁵），比如，计算 $L$ 关于 $z$ 的偏导数 $\frac{\delta L}{\delta z}$ (即，由 $L(\hat{y},y)\to \hat{y}=\sigma (z)$）的过程如下：
$$\frac{\delta L(\hat{y},y)}{\delta z}=\frac{\delta L(\hat{y},y)}{\delta \hat{y}}\times \frac{\delta \hat{y}}{\delta z}$$
此外，图 3 中的计算使用到了 log函数、Sigmoid 函数，以及函数和、积的求导法则，在此篇中不过多介绍，感兴趣的可以参阅：初等函数求导法则⁶ 自行查阅，看看你能否计算出以下的结果呢？

其余反向传导过程依此类推，直至到输入端，即可得到：
$$\begin{array}{rl}\delta {\theta }_0& =\delta z=\hat{y}-y=h_{\theta }(x)-y\\ \delta {\theta }_1& =x_1\cdot \delta z\\ \delta {\theta }_2& =x_2\cdot \delta z\end{array}$$

图3 通过计算图来理解逻辑回归梯度下降算法

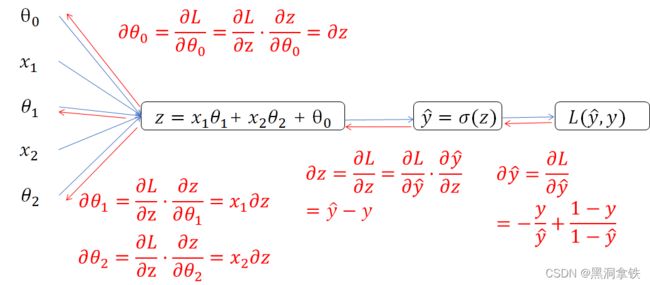
逻辑回归梯度下降算法

以上，我们详细介绍了在只有一个样本的情况下，如何通过计算图辅助我们理解偏导数 $\frac{\delta }{\delta {\theta }_j}J(\Theta )$ 的计算过程。对于更一般的情况，即有 $m$ 个样本的情况，偏导数的计算公式如下：
$$\frac{\delta }{\delta {\theta }_j}J(\Theta )=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_j^{(i)}$$
逻辑回归梯度下降算法的形式如下（在每次迭代过程中，同时更新所有 ${\theta }_j$，学习率为 $\alpha$）：
$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_j^{(i)}$$
仔细观察一下，上式和线性回归梯度下降算法更新参数的表达式是类似的！只不过，在此式中 $h_{\theta }(x)$ 的表达式变了 ，即$h_{\theta }(x^{(i)})=\sigma ({\Theta }^T{x}^{(i)})$。

逻辑回归二分类实例

有了上述的知识储备，我们来具体看一下，如何通过逻辑回归训练一个学生录取概率的预测模型。

在开始执行任何算法之前，如果可能的话，一般的做法是先直观地了解一下数据的分布情况。在下图 4 中，横纵轴分别为科目一（Exam 1 score）、科目二的考试成绩（Exam 2 score），其中蓝色点代表被录取的学生，红色点代表未被录取的学生。逻辑回归要解决的就是找到一条分界线，区分上述两类样本。

图4 学生录取预测数据可视化

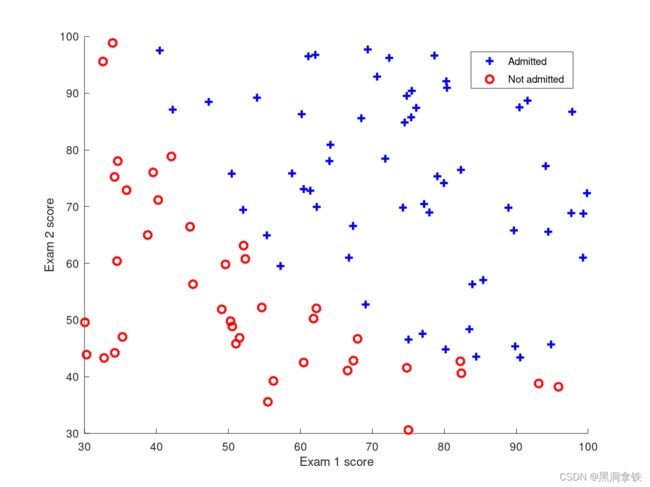
类似于线性回归，你采用逻辑回归算法构建了函数假设 $h_{\theta }(x)$、定义了损失函数 $J(\Theta )$，并应用梯度下降算法寻找最小化 $J(\Theta )$ 的参数组合 $\Theta$。算法最终优化得到的 $\Theta$ 值组合为，{${\theta }_0,{\theta }_1,{\theta }_2$} = {-25.161, -0.206, -0.201}，即：
$$h_{\theta }(x)=\sigma (-25.161-0.206Exam\_1score-0.201Exam\_2score)$$
其中，$-25.161-0.206Exam\_1score-0.201Exam\_2score=0$ 即为区分是否录取的决策边界，即为下图 5 中的黄色直线。

图5 学生录取预测决策边界

接下来，我们就可以使用训练好的模型来预测特定的学生是否会被录取。比如，某学生科目一、科目二考试成绩分别为 45 分和 85 分，计算得到其录取概率为 0.776，即 $h(45,85)=\sigma (-25.161-0.206\times 45-0.201\times 85)=\sigma (1.194)\approx 0.776$。

那么，以上得到的是一个理想的决策边界吗？从图中可以直观地看到，在这样的决策边界下，边界附近的一些点并没有被正确地分类。如果统计一下训练样本中被正确分类的样本所占的比例，可以得到我们构建的分类器的准确率为 89%，显然还有提升空间。

为什么我们构建的分类器效果不够理想呢？从上图 5 中可以看到，红蓝点之间的分界更近似于一条曲线，而我们构建的分类器是一个线性的分类器，其决策边界是一条直线（因为我们只使用了输入特征 $x$ 的一次项）。为了得到一个非线性的决策边界，我们可以尝试：

1， 类似于在线性回归模型中介绍的方法，可以通过构建输入特征的多项式项来刻画非线性关系，比如加入 $x_1^2$，$x_1{x}_2$, $\sqrt{x_2}$ … 当然，具体加入哪些项，还需根据模型最终效果来决定。

2， 使用更复杂的模型，比如神经网络，关于构建非线性分类器的部分，我们将在后续的文章中介绍。

小结

在此篇文章中，我们主要介绍了以下三点内容：

1， 逻辑回归是一种分类算法，其基于现有数据对不同类别间的决策边界线建立回归公式，以此区分不同类别。

2， 相比于线性回归，逻辑回归通过 Sigmoid 函数将模型预测值映射至 0 和 1 之间，其输出表示样本属于某一类别的概率。

3， 同样可以通过梯度下降算法求得最优参数 $\Theta$ 以最小化逻辑回归损失函数 $J(\Theta )$，计算图可以帮助理解梯度的计算过程。

Logistic回归优点：

• 不仅能预测出“类别”，还可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用。
• 计算代价不高，易于理解和实现。

缺点：

• 拟合效果欠佳，分类精度可能不高。

参考资料

---

1. 数据来自吴恩达机器学习课程 ↩︎

2. 周志华. 机器学习[M]. 清华大学出版社, 2016. ↩︎

3. Harrington P. 机器学习实战[J]. 人民邮电出版社, 北京, 2013. ↩︎

4. 吴恩达. Deep learning and neural network. ↩︎

5. 复合函数求导链式法则. ↩︎

6. 初等函数求导法则. ↩︎