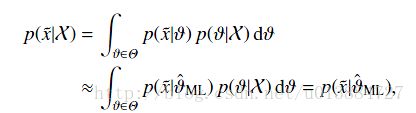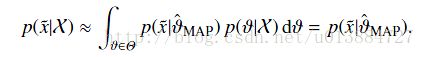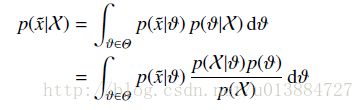经验风险最小化、结构风险最小化、极大似然估计、最大后验概率估计...||《统计学习方法》李航_第1章_蓝皮(学习笔记)
第1章 统计学习方法概论
- 监督学习
- 统计学习三要素
-
- 模型
- 策略(经验风险和结构经验风险)
- 判别模型与生成模型
- 补充(含课后作业)
-
- MLE、MAP和贝叶斯估计
- 证明经验风险最小化等价于极大似然估计(在特定条件下)
- 证明结构风险最小化与最大后验概率等价(在特定条件下)
- 贝叶斯估计
挑重点记录一下。
监督学习
监督学习有一个重要的假设:设输入的随机变量 X X X和 Y Y Y遵循联合概率分布 P ( X , Y ) P\left( {X,Y} \right) P(X,Y),所有数据是独立同分布的。
统计学习三要素
包括模型、策略、算法(书中算法没有细讲)
模型
在监督学习过程中,模型是要学习的条件概率分布或者决策函数。模型的假设空间记为 F \mathcal F F。
- 假设空间包括决策函数的集合: F \mathcal F F = { f ∣ Y = f ( X ) } \{ \it f \ | \ Y=\it f (X)\} {f ∣ Y=f(X)}
F \mathcal F F 通常是有参数 θ \theta θ决定的: F \mathcal F F = { f ∣ Y = f θ ( X ) , θ ∈ R n } \{ \it f\ |\ Y=\it f_\theta (X),\theta \in \bf R^n \} {f ∣ Y=fθ(X),θ∈Rn} - 假设空间是条件概率的集合: F \mathcal F F = { P ∣ P ( Y ∣ X ) } \{P\ |\ P ( Y|X ) \} {P ∣ P(Y∣X)}
F \mathcal F F 通常是有参数 θ \theta θ决定的: F \mathcal F F = { P ∣ P θ ( Y ∣ X ) , θ ∈ R n } \{P\ |\ P_\theta ( Y|X ), \theta \in \bf R^n \} {P ∣ Pθ(Y∣X),θ∈Rn}
策略(经验风险和结构经验风险)
有了模型,就要考虑按照什么准则学习,或者如何选择最优模型
-
损失函数和风险函数
●损失函数一般指衡量预测值 f ( X ) \it f (X) f(X)和真实 Y Y Y之间差异,常用的有:
(1)平方误差: L ( Y , f ( X ) ) = ( Y − f ( X ) ) 2 L(Y, \it f(X)) = (Y - \it f (X))^2 L(Y,f(X))=(Y−f(X))2
(2)对数似然函数: L ( Y , f ( X ) ) = − l o g P ( Y ∣ X ) L(Y, \it f(X)) = -log P(Y | X) L(Y,f(X))=−logP(Y∣X)
●风险函数指理论上模型 f ( X ) \it f (X) f(X)关于 P ( X , Y ) P( X,Y ) P(X,Y)的期望:
R e x p ( f ) = E p [ L ( Y , f ( X ) ) ] R_{exp} (f) = E_p[L(Y, \it f(X)) ] Rexp(f)=Ep[L(Y,f(X))] = ∫ x , y L ( y , f ( x ) ) P ( x , y ) d x d y \int_{x,y}^{}\ {L(y, \it f(x))P( x,y )}\ dxdy ∫x,y L(y,f(x))P(x,y) dxdy
然而,我们没有那么多数据,所以引出了: -
经验风险和结构经验风险
●经验风险就是在给定的N个数据 ( x i , y i ) , i ∈ { 1... N } (x_i,y_i),i \in \{1...N\} (xi,yi),i∈{1...N}情况下,利用大数定律,用经验风险逼近期望风险,公式如下:
R e m p ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) R_{emp}(f) = \frac {1} {N} \sum_{i=1}^{N} {L(y_i, \it f(x_i))} Remp(f)=N1∑i=1NL(yi,f(xi))
但是由于样本不多,所以引入结构风险:
●结构风险是为了防止过拟合(在样本数量不足但参数过多时容易过拟合,公式如下:
R s r m ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f ) R_{srm}(f) = \frac {1} {N} \sum_{i=1}^{N} {L(y_i, \it f(x_i))} \ +\ \lambda J(\it f) Rsrm(f)=N1∑i=1NL(yi,f(xi)) + λJ(f)
J ( f ) J(\it f) J(f)是复杂度,模型越复杂, J ( f ) J(\it f) J(f)就越大,也就是说复杂度表示了对复杂模型的惩罚。
因此我们的策略就是求解最小化经验风险或者结构风险:
min f ∈ F 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f ) \min \limits_{\it f \in \mathcal F} \ \frac {1} {N} \sum_{i=1}^{N} {L(y_i, \it f(x_i))} \ +\ \lambda J(\it f) f∈Fmin N1∑i=1NL(yi,f(xi)) + λJ(f)
另外,
当 模 型 是 条 件 概 率 分 布 , 损 失 函 数 是 负 对 数 函 数 时 , 经 验 风 险 最 小 化 等 价 于 极 大 似 然 估 计 ( M L E ) ; \color{Red}{当模型是条件概率分布,损失函数是负对数函数时,经验风险最小化等价于极大似然估计(MLE);} 当模型是条件概率分布,损失函数是负对数函数时,经验风险最小化等价于极大似然估计(MLE);
结 构 风 险 最 小 化 等 价 于 最 大 后 验 概 率 估 计 ( M A P ) \color{Red}{结构风险最小化等价于最大后验概率估计(MAP)} 结构风险最小化等价于最大后验概率估计(MAP) . . . . . . . . 后面会证明。
判别模型与生成模型
- 生成方法
由数据学习得到联合概率分布 P ( X , Y ) P\left( {X,Y} \right) P(X,Y),然后求出条件概率分布 P ( Y ∣ X ) P(Y | X) P(Y∣X)
主要模型有:朴素贝叶斯模型和隐马尔可夫模型,比较难。 - 判别方法
由数据直接学习 P ( Y ∣ X ) P(Y | X) P(Y∣X)或者判别函数 f ( X ) \it f (X) f(X)
主要模型有:k近邻、感知器、决策树、逻辑回归、最大熵模型、SVM、条件随机场等。
补充(含课后作业)
先介绍一下极大似然估计、最大后验概率估计以及贝叶斯估计(每次看见这几个都有点恍惚,这次要全部弄懂!)
MLE、MAP和贝叶斯估计
首先弄明白估计是在估计什么:三种估计都是对概率分布的参数进行求解,比如高斯分布的均值 μ \mu μ、方差 σ \sigma σ或者伯努利分布的概率 p p p,以上所有都用 θ \theta θ代替。
也就是说,我们可能有一堆数据,知道 P ( X ∣ θ ) P(X|\theta) P(X∣θ)(求参数),其中 θ \theta θ是变量,那怎么求(找策略),所以有三种策略,极大似然估计、MAP和贝叶斯估计。
因为经常搞不清条件概率和似然函数的区别,所以查了很多资料,下面这个理解感觉能解释得通:
对于这个函数: P(x|θ)
P(x|θ) 输入有两个:x表示某一个具体的数据;θ表示模型的参数。
如果θ是已知确定的,x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点x,其出现概率是多少。
如果x是已知确定的,θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现x这个样本点的概率是多少。
举例(作业题):求N次独立伯努利实验下,结果中有k次的结果为1(说明所有x已知),估计结果为1的概率(求参数)。
其中伯努利分布是一个0-1分布,即P(x=1)=θ, P(x=0)=1-θ;
对应的似然就是P(x=1 | θ)=θ, P(x=0 | θ)=1-θ;(注意是小写x)
证明经验风险最小化等价于极大似然估计(在特定条件下)
1. 极大似然估计
所以依据所有实验数据, 似 然 函 数 等 于 所 有 似 然 概 率 的 乘 积 \color{Red}{似然函数等于所有似然概率的乘积} 似然函数等于所有似然概率的乘积(一般都是这样定义),加上我们独立同分布的假设,得到似然函数(注意我们求解的依然是条件概率):
L ( θ ∣ X ) = P ( X ∣ θ ) = ∏ i = 1 N P ( x i ∣ θ ) L(\theta | X)=P(X|\theta) = \prod_{i=1}^{N}{P(x_i|\theta)} L(θ∣X)=P(X∣θ)=∏i=1NP(xi∣θ)
我们一般写成对数形式,方便求解,即,
L ( θ ∣ X ) = ∑ i = 1 N l n P ( x i ∣ θ ) L(\theta | X)= \sum_{i=1}^{N}{lnP(x_i|\theta)} L(θ∣X)=∑i=1NlnP(xi∣θ)
极大似然估计,就是求使得似然函数概率最大的值,则我们得到优化函数:
max θ L ( θ ∣ X ) = max θ ∑ i = 1 N l n P ( x i ∣ θ ) \max \limits_{\theta} L(\theta | X)=\max \limits_{\theta} \sum_{i=1}^{N}{lnP(x_i|\theta)} θmaxL(θ∣X)=θmax∑i=1NlnP(xi∣θ)
取负对数:
min θ L ( θ ∣ X ) = min θ ∑ i = 1 N − l n P ( x i ∣ θ ) \min \limits_{\theta} L(\theta | X)=\min \limits_{\theta} \sum_{i=1}^{N}{-lnP(x_i|\theta)} θminL(θ∣X)=θmin∑i=1N−lnP(xi∣θ)
比较经验风险最小化: min f ∈ F 1 N ∑ i = 1 N L ( y i , f ( x i ) ) \min \limits_{\it f \in \mathcal F} \ \frac {1} {N} \sum_{i=1}^{N} {L(y_i, \it f(x_i))} f∈Fmin N1∑i=1NL(yi,f(xi))
可 以 看 到 极 大 似 然 估 计 取 负 对 数 时 与 经 验 风 险 最 小 化 等 价 \color{Red}{可以看到极大似然估计取负对数时与经验风险最小化等价} 可以看到极大似然估计取负对数时与经验风险最小化等价
求解的算法就是求导,另导数为0即可得到最优 θ ∗ \theta^* θ∗
得到 θ \theta θ的目的也是为了预测,我们的最终目的是去预测新事件基于这个参数下发生的概率:
因为是估计值,所以是约等于
因此,带入作业可以得到
L ( θ ) = ∏ i = 1 N P ( x i ∣ θ ) = θ k ( 1 − θ ) N − k L(\theta) = \prod_{i=1}^{N}{P(x_i|\theta)} = {\theta}^k {(1-\theta)}^{N-k} L(θ)=∏i=1NP(xi∣θ)=θk(1−θ)N−k
对数形式为
L ( θ ∣ X ) = ∑ i = 1 N l n P ( x i ∣ θ ) = l n θ k ( 1 − θ ) N − k L(\theta | X)= \sum_{i=1}^{N}{lnP(x_i|\theta)} = ln {\theta}^k {(1-\theta)}^{N-k} L(θ∣X)=∑i=1NlnP(xi∣θ)=lnθk(1−θ)N−k
求导赋0得
k l n θ + ( N − k ) l n ( 1 − θ ) = 0 kln\theta + (N-k)ln(1-\theta)=0 klnθ+(N−k)ln(1−θ)=0
解得
θ ∗ = k N \theta^* = \frac{k}{N} θ∗=Nk
可以看出,极大似然估计以实验中概率大的结果,没有考虑先验信息等。因此提出最大后验概率策略。
证明结构风险最小化与最大后验概率等价(在特定条件下)
2.最大后验概率估计
最大后验概率引入了参数的先验概率,根据贝叶斯公式,后验概率为:
P ( θ ∣ X ) = P ( X ∣ θ ) P ( θ ) / P ( X ) P(\theta|X)= {P(X|\theta) P(\theta)}/{P(X)} P(θ∣X)=P(X∣θ)P(θ)/P(X),但在一个实验中,如N次伯努利实验,正反面的概率已知,所以 P ( X ) P(X) P(X)是已知的。因此我们可以认为最大后验概率是求 P ( X ∣ θ ) P ( θ ) P(X|\theta)P(\theta) P(X∣θ)P(θ)最大。
此时的似然函数为:
L ( θ ∣ X ) = P ( θ ∣ X ) ∝ ∏ i = 1 N P ( x i ∣ θ ) P ( θ ) L(\theta | X)=P(\theta|X) \propto \prod_{i=1}^{N}{P(x_i|\theta)P(\theta)} L(θ∣X)=P(θ∣X)∝∏i=1NP(xi∣θ)P(θ)
对数形式为:
L ( θ ∣ X ) = ∑ i = 1 N l n P ( x i ∣ θ ) + l n P ( θ ) L(\theta | X)= \sum_{i=1}^{N}{lnP(x_i|\theta)+lnP(\theta)} L(θ∣X)=∑i=1NlnP(xi∣θ)+lnP(θ)
优化函数:
max θ L ( θ ∣ X ) = max θ ∑ i = 1 N l n P ( x i ∣ θ ) + l n P ( θ ) \max \limits_{\theta} L(\theta | X)=\max \limits_{\theta} \sum_{i=1}^{N}{lnP(x_i|\theta) + lnP(\theta)} θmaxL(θ∣X)=θmax∑i=1NlnP(xi∣θ)+lnP(θ)
取负对数:
min θ L ( θ ∣ X ) = min θ − { ∑ i = 1 N l n P ( x i ∣ θ ) + l n P ( θ ) \min \limits_{\theta} L(\theta | X)=\min \limits_{\theta}- \{\sum_{i=1}^{N}{lnP(x_i|\theta) + lnP(\theta)} θminL(θ∣X)=θmin−{∑i=1NlnP(xi∣θ)+lnP(θ)}
比较结构风险最小化:
min f ∈ F 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f ) \min \limits_{\it f \in \mathcal F} \ \frac {1} {N} \sum_{i=1}^{N} {L(y_i, \it f(x_i))} \ +\ \lambda J(\it f) f∈Fmin N1∑i=1NL(yi,f(xi)) + λJ(f)
可 以 看 到 最 大 后 验 概 率 估 计 取 负 对 数 时 与 结 构 风 险 最 小 化 等 价 \color{Red}{可以看到最大后验概率估计取负对数时与结构风险最小化等价} 可以看到最大后验概率估计取负对数时与结构风险最小化等价
求解的算法还是求导,得到一个最优 θ ∗ \theta^* θ∗
贝叶斯估计
完全参考贝叶斯估计
总结一下就是,不求 θ \theta θ,求出后验分布出来
其他参考:
https://blog.csdn.net/u011508640/article/details/72815981
https://blog.csdn.net/u013884727/article/details/23544633