聊一聊那些激活函数
文章目录
-
- 神经网络和神经元
- 激活函数
-
- 为什么要用
- 有什么激活函数
- 重点介绍
-
- Mish
- Sigmoid
- TanH
- Relu
- Leaky ReLU
- SoftPlus
- Bent Identity
- Swish
- 如下为上述激活函数的可视化图
- 如何选择
神经网络和神经元
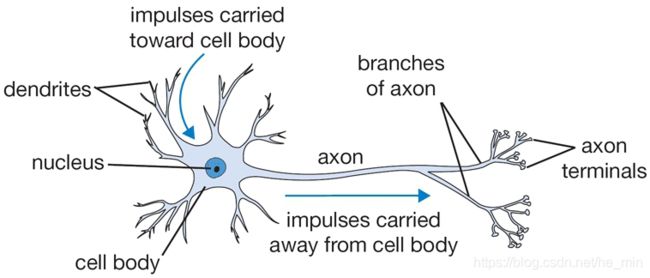
如今,一说起人工智能,都会说两句深度学习大法好!说起深度学习就不得不提起神经网络,不管是之前的BP(back propagation),还是现在的CNN(Convolutional Neural Networks).都是一种仿生设计,模仿的人类的神经元处理过程以及眼睛的局部感受野。从生物书上可以了解到,人的神经系统中大概有860亿个神经元,这些神经元通很多的突触连接起来。每个神经元从树突接受到信号,然后沿着轴突传递信号,而神经网络中可以这么理解:突触控制着传导到下一个神经元的信号强弱(权重), 如果传递到下一个神经元的数值超过了一定的阈值,那么这个神经元被激活,同时继续传递信号,这个激活就是这篇文章的重点, 在神经网络中叫做激活函数,用来控制着对神经元的激励程度, 从而控制着是否向后传递信号。
激活函数
为什么要用
对于
y = a x + b y=ax+b y=ax+b
这样的函数,当x的输入很大时,y的输出也是无限大,经过多层网络叠加后,值会越累越大,这显然不符合预期,很多情况下我们希望的输出是一个概率。 线性函数的表达能力太有限了,即使经过多层网络的叠加,最后仍然是线性的,增加网络的深度根本没有意义。线性回归连下面这个最简单的“异或”都无法拟合。
因为线性模型的表达能力不够。需要加入激活函数是来引入非线性因素,
有什么激活函数
- ReLU
- Sigmoid
- Tanh
- GELU
- Leaky ReLU
- Swish
- PReLU
- GLU
- Softplus
- Maxout
- ELU
- Mish
- ReLU6
- Hard Swish
- SELU
- Softsign
- Shifted Softplus
- CReLU
- RReLU
- Hard Sigmoid
- KAF
- TanhExp
- SiLU
- SReLU
- modReLU
- Hermite
- E-swish
- m-arcsinh
- PELU
- ELiSH
- HardELiSH
- SERLU
- ARiA
- nlsig
- Lecuns Tanh
- Hardtanh
重点介绍
Mish
Mish 是神经网络的一种激活函数,这个激活函数的定义是:
f ( x ) = x ⋅ t a n h ⋅ s o f t p l u s ( x ) f(x) = x\cdot tanh\cdot softplus(x) f(x)=x⋅tanh⋅softplus(x)
其中:
s o f t p l u s ( x ) = l n ( 1 + e x ) softplus(x) = ln(1+e^x) softplus(x)=ln(1+ex)
Sigmoid
sigmoid 是神经网络中常用的一种激活函数,它的定义是
f ( x ) = 1 1 + e x p ( − x ) f(x)=\frac{1}{1+exp(-x)} f(x)=1+exp(−x)1
有些文献指出这个激活函数的缺点,从较深的隐含层往输入层反向传播的过程中, 容易导致梯度包和,收敛缓慢。
TanH
历史上,tanh函数比sigmoid函数更受欢迎,因为它能为多层神经网络提供更好的性能。但它并没有解决sigmoid所面临的消失弥散问题,通过引入ReLU激活,这一问题得到了更有效的解决。
Tanh的数学表达式为:
f ( x ) = e x − e − x e x + e − x f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} f(x)=ex+e−xex−e−x
Relu
Relu 是常见的一个激活函数, 它的正半轴是线性的,而负半轴却是0 , 相比于sigmoid, Relu 可以有效的避免梯度弥散, 该激活函数的数学公式为:
f ( x ) = m a x ( x , 0 ) f(x)=max(x, 0) f(x)=max(x,0)
Leaky ReLU
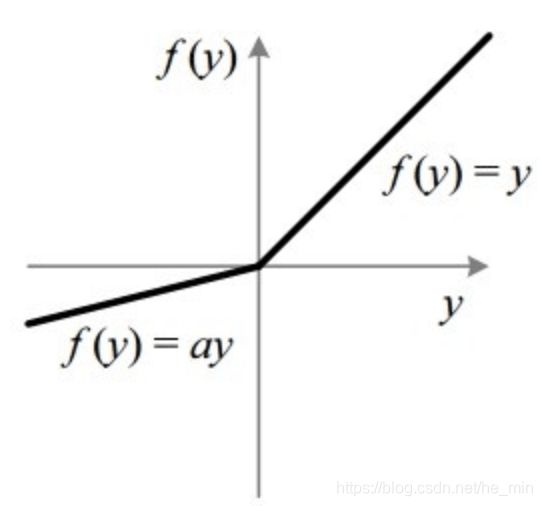
LeakyReLU 是一种基于ReLU的激活函数,但它的负值斜率很小,而不是平坦的斜率。斜率系数需要在训练前确定,即在训练过程中不学习。这种类型的激活函数在可能遇到稀疏梯度的任务中很流行,例如训练生成式对抗网络。该激活函数的直观表述为:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6gQW6Y9C-1609482685875)(http://bed.thunisoft.com:9000/ibed/2021/01/01/BQByo3Aps.png)]
SoftPlus
该激活函数可以看作是光滑的Relu, 它的数学表达式为:
f ( x ) = l o g ( 1 + e x p ( x ) ) f(x)=log(1+exp(x)) f(x)=log(1+exp(x))
Bent Identity
激活函数 Bent Identity 是介于 Identity 与 ReLU 之间的一种折衷选择。它允许非线性行为,尽管其非零导数有效提升了学习并克服了与 ReLU 相关的静默神经元的问题。由于其导数可在 1 的任意一侧返回值,因此它可能容易受到梯度爆炸和消失的影响。
Swish
swish的表达式为:
f ( x ) = x ⋅ s i g m o i d ( b x ) f(x)=x\cdot sigmoid(bx) f(x)=x⋅sigmoid(bx)
其中b是可学参数, Swish 具备无上界有下界、平滑、非单调的特性。Swish 在深层模型上的效果优于 ReLU。例如,仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%,Inception-ResNet-v 的分类准确率提高 0.6%。
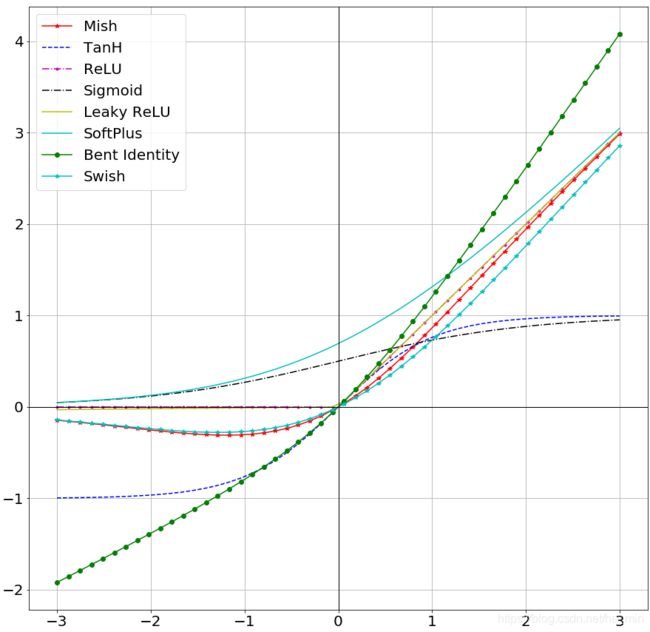
如下为上述激活函数的可视化图
如何选择
已经有了这么多的激活函数,接下来就需要分析在哪种情况下应该使用哪种激活函数,激活函数效果,不能凭感觉定论。然而,根据问题的性质,我们可以为神经网络更快更方便地收敛作出更好的选择。
用于分类器时,Sigmoid函数及其组合通常效果更好。由于梯度消失问题,有时要避免使用sigmoid和tanh函数。ReLU函数是一个通用的激活函数,目前在大多数情况下使用。如果神经网络中出现死神经元,那么PReLU函数就是最好的选择.其中ReLU函数只能在隐藏层中使用。