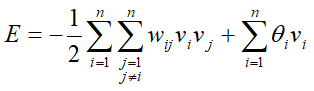机器学习——期末复习
文章目录
-
-
-
- 填空题
-
- 第一章 机器学习基础
- 第二章 数据预处理
- KNN算法
- 支持向量机
- 集成学习
- 决策树
- 聚类算法
- 联结学习
- 三种池化操作
- 选择题
- 计算题
-
- 数据正规化
- Hopfield网络能量函数计算
- 卷积、池化操作
- 应用题
-
- 决策树、朴素贝叶斯、聚类算法
- 单层感知器构造（连接神经元部分）
-
-
填空题
第一章 机器学习基础
按机器学习系统的含义：是指能够在一定程度上实现机器学习系统
机器学习按对人类学习的模拟方式：符号主义学习、统计学习、连接主义学习等。
学习系统基本模型4部分：
机器学习任务：1、分类、回归、聚类 2、降维、去噪 3、机器翻译、异常检测
机器学习基本流程：数据处理、训练、验证、预测
数据集划分（判断是哪个数据集）：训练集。用于训练模型。验证集。用于调整模型。测试集。用于评估模型
模型效果描述（给出意义描述写术语）：拟合是模型与训练数据和测试数据具有较好的拟合性、过拟合是指的是模型出现拟合过度的情况。过拟合表现为模型在训练数据中表现良好，在预测时却表现较差、欠拟合是欠拟合是指在训练数据和预测结果时，模型精确度均不高的情况。
机器学习三种类型（区分分类和回归、聚类和降维概念）：
- 监督学习：监督学习算法是给定一组输入x和输出y的训练集，学习如何关联输入和输出
- 分类： 分类任务是对离散结果的预也就是提供的标签是离散的。
- 回归：回归任务是对连续结果的预测也就是提供的标签是连续的。
- 无监督学习：
- 聚类：聚类是将数据集中的样本划分为若干个不相交的子集(簇)，每个簇可能对应于一些潜在的概念
- 降维：在高维情况下出现的数据样本稀疏、距离计算困难等问题被称为维度灾难,解决维度灾难的一个途径就是降维。降维是将原始高维空间转变为一个低维空间即高维空间的一个低维嵌入。
- 强化学习：就是一个智能体采取行动从而改变自己的状态获得奖励与环境发生交互的循环过程。
模型性能描述
- 准确率、查准率、查全率
- 准确率：分类正确的样本占总样本的比例
- 查准率：正确被检索的样本占所有实际被检索得到的样本的比例
- 查全率：正确被检索出的样本占所有应该检索的样本的比例
- MSE、RMSE
- F1、ROC
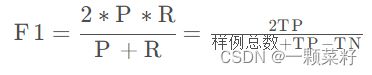
第二章 数据预处理
数据预处理（3个给定义写术语）：数据清理、数据转换、数据压缩
-
数据清洗( Data Cleaning ) 主要是通过填补缺失值、光滑噪声数据，平滑或删除离群点，并解决数据的不一致性来“清理”数据。自然数据中的异常值等问题可能会影响机器学习模型并产生有偏差的结果。常见问题数据如下：
+ 缺失值：它指的是现有数据集中某个或某些属性的值是不完全的，可能直接导致算法无法直接分析数据。
+ 离群值：它指在一份数据中,与其他观察值具有明显不同特征的那些观察值，可能会使数据的分布失真影响模型判断。 -
数据转换:数据转换（Data Transformation）就是修改数据的表示形式，使其符合机器学习模型的输入要求，并使机器学习模型的优化算法更容易生效。
- 数字化：一般在计算型任务中需要用数值特征，因此会遇到非数值特征转换为数值特征情况。
- 离散化：有时数据为连续值，而模型只能处理离散型数据，则需要将连续数据转换为离散数据。
- 正规化：数据压缩到一个范围内赋予所有属性相等的权重，进行规范化处理。
- 数值转换：数值变换能够增加数据的非线性特征捕获特征之间的关系，有效提高模型的复杂度。
-
数据压缩：数据压缩是一种有助于减少数据集的数据量或维数或两者兼得的技术，从而使模型的学习过程更加有效，并帮助模型获得更好的性能，防止过度拟合问题并修复不均匀的数据分布
- 降维：将高维数据转换为低维，有利于模型计算和可视化等操作
- 实例选择和采样：通过减少数据样本，寻求以最小的性能损失来训练模型的机会。如通过K近邻分类算法选择实例，随机采样收集部分样本。
KNN算法
给定义写术语：它根据距离函数计算待分类样本X和每个训练样本的距离（作为相似度），选择与待分类样本距离最小的K个样本作为X的K个最近邻，最后以X的K个最近邻中的大多数样本所属的类别作为X的类别。
三大步骤：算距离、找邻居、做分类
支持向量机
最常使用的四类核函数：
集成学习
集成学习给定义写术语： 集成学习是指为解决同一问题，先训练出一系列个体学习器（或称弱学习器），然后再根据某种规则把这些个体学习器的学习结果整合到一起，得到比单个个体学习器更好的学习效果
集成学习两大基本问题：一个是个体学习器的构造，另一个是个体学习器的合成。
集成学习分类：Boosting方法和Bagging方法两大基本类
决策树
给定义写术语：决策树分类方法采用自顶向下的递归方式，在决策树的内部节点进行属性值的比较，根据不同的属性值判断从该节点向下的分支，在决策树的叶节点得到结论。
常用决策树算法：ID3、C4.5、CART（区分概念，谁取最大或最小）
ID3：按信息增益划分
C4.5：增益比例
CART：基尼指数
聚类算法
K-means、K-中心点、DBSCAN
联结学习
人工神经网络给定义写术语：人工神经网络是一种对人工神经元进行互联所形成的网络，它是对生物神经网络的模拟。反映的是神经元的饱和特性
人工神经网络分类（重点按拓扑和按学习方法）
常见网络：深度卷积神经网络、深度波尔兹曼机、深度信念网络
深度神经网络给定义写术语：深层神经网络也叫深度神经网络（DNN），通常是指隐含层神经元不少于2层的神经网络，目前可做到数百层甚至更多
正向传播过程3个操作、反向传播过程2个
三种池化操作
最大池化、最小池化、均值池化
选择题
计算题
数据正规化
- 使用min-max方法规范化数据组：200，300，400，600，1000的结果分别是
- 假定属性平均家庭总收入的均值和标准差分别为9000元和2400元，值12600元使用z-score规范化转换结果为
- 假定A的取值范围是-1075~923。使用十进制缩放规范化方法转换-1075结果为： ，923转换结果为：
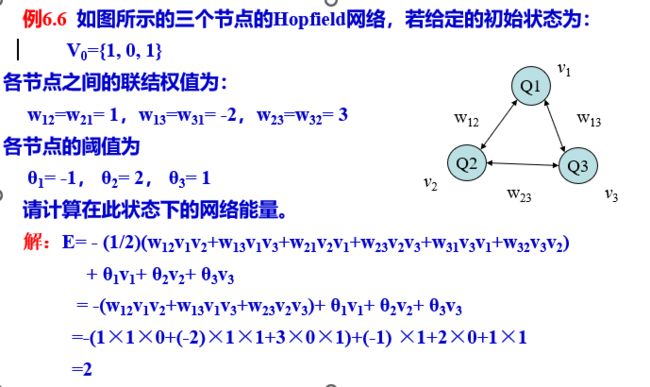
Hopfield网络能量函数计算
Hopfield 网络的能量函数定义如下：
式中；n是网络中的神经元个数，wij 是神经元i和神经元 j之间的连接权值，且有wij = wji ； vi和 vj分别是神经元i和神经元 j 的输出；θi 是神经元i的阈值。
卷积、池化操作
卷积操作
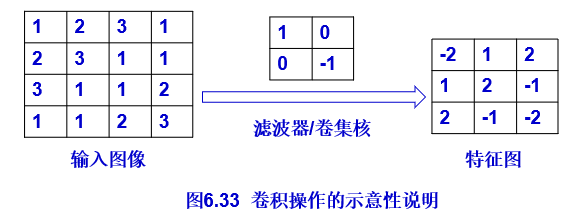
池化操作
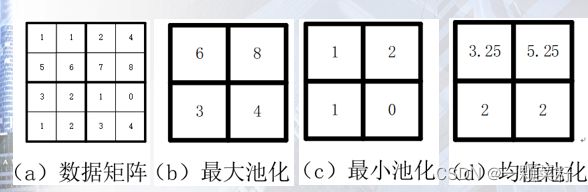
卷积、池化操作所得特征图的尺寸
卷积：
特征矩阵的行数和列数:假设数据矩阵大小为M×N，卷积核大小为m×n，填充的圈数为p，水平方向和竖直方向的步长分别为 d 1 , d 2 d_1,d_2 d1,d2，则有特征矩阵的行数和列数分别为：
池化
M×N，池化窗口大小为m×n =》 R = M / m, C = N / n
应用题
决策树、朴素贝叶斯、聚类算法
单层感知器构造（连接神经元部分）
试根据训练集：
D = ( ( 1 , 2 ) T , 1 ) , ( ( 3 , 3 ) T , 1 ) , ( ( 2 , 1 ) T , − 1 ) , ( ( 5 , 2 ) T , − 1 ) D={((1,2)^T,1),((3,3)^T,1),((2,1)^T,-1),((5,2)^T,-1)} D=((1,2)T,1),((3,3)T,1),((2,1)T,−1),((5,2)T,−1)构造一个感知机模型，学习率α=1。
【解】已知感知机模型的具体形式为： f ( X ) = s g n ( W T X ) f(X)=sgn(W^T X) f(X)=sgn(WTX)
s g n ( t ) = { 1 , ( t > = 0 ) − 1 , ( t < 0 ) sgn(t)= \left\{ \begin{array}{ lr } 1, &(t>=0) \\ -1, &(t < 0)\\ \end{array} \right. sgn(t)={1,−1,(t>=0)(t<0)
其中 W = ( b , w 1 , w 2 ) T , X = ( 1 , x 1 , x 2 ) T W=(b,w_1,w_2 )^T,X=(1,x_1,x_2 )^T W=(b,w1,w2)T,X=(1,x1,x2)T。使用数据集D构造感知机模型的具体步骤如下：
(1)初始化参数向量 W = ( 0 , 0 , 0 ) T W=(0,0,0)^T W=(0,0,0)T
(2)随机选择一个样本 ( ( 2 , 1 ) T , − 1 ) ((2,1)^T,-1) ((2,1)T,−1)输入初始模型，求得 f ( X = ( 2 , 1 ) T ) = s g n ( 0 ) = 1 ≠ − 1 f(X=(2,1)^T )=sgn(0)=1≠-1 f(X=(2,1)T)=sgn(0)=1=−1,该样本未被感知机模型正确分类，使用如下公式更新模型参数：
w i = w i + α y i x i , b = b + α y i w_i=w_i+αy_i x_i, b=b+αy_i wi=wi+αyixi,b=b+αyi
计算得到新的参数向量 W = ( − 1 , − 2 , − 1 ) T W=(-1 ,-2,-1)^T W=(−1,−2,−1)T，获得的感知机模型为:
f ( X ) = s g n ( − 2 x 1 − x 2 − 1 ) f(X)=sgn(-2x_1-x_2-1) f(X)=sgn(−2x1−x2−1)
将数据集D中样本均输入更新后的感知机模型中，若存在样本被错误分类，则根据步骤（2）中公式进行参数更新，直至D中所有样本均分类正确时结束算法并输出模型。