【Paper Quickthrough】2021 Bert 各向异性

Bert各向异性2021 Paper Quickthrough

ISOTROPY IN THE CONTEXTUAL EMBEDDING SPACE: CLUSTERS AND MANIFOLDS

Paper Url. Github Url. Accepted by ICLR 2021.

Abstract

近年来，深度语言模型(如BERT和ERNIE)的上下文嵌入空间的几何特性受到了广泛关注。对上下文嵌入的研究表明，空间具有很强的各向异性，大多数向量落在一个狭窄的锥内，导致高余弦相似性。令人惊讶的是，这些语言模型能够如此成功，因为它们的大多数嵌入向量彼此都非常相似。在本文中，我们从一个不同但更有建设性的角度，论证了空间中确实存在各向同性。我们在上下文嵌入空间中识别出孤立的簇和低维流形，并引入了定性和定量分析它们的工具。我们希望本文的研究能为我们更好地理解深层语言模型提供一些启示

1. Intuition

虽然Bert向量在很多任务上变现的很棒，但是由于其向量退化的特性，即所有的高维向量空间都是在一个凸锥中，所以在计算余弦距离时计算的值都很大。

所以本文通过各向异性的角度进行探究得到了以下几点结论：

1)我们在向量空间中发现了簇类内的各向同性，这与之前的学术研究的各向异性(由误导的孤立聚类造成)形成了对比。通过引入clustering和center shifting的方法来揭示各向同性，并在跨模型之间显示了更一致layer-wise行为。

2)在GPT/GPT2嵌入中发现Swiss-Roll流形，但在BERT/DistilBERT嵌入中没有发现。流行与词频分布密相关，这表明当模型看到更多数据时，其演变方式有所不同。我们使用Local Intrinsic Dimension (LID)来描述流形，并发现上下文嵌入模型，包括所有BERT、GPT族和ELMo，通常都有小的LIDs。小LID可以视空间的局部各向异性。

什么是Local Intrinsic Dimension (LID)?

简单点来说就是描述data on manifold的最少需要的变量的个数。

如链接中例图，数据本身的表示是三维的，可以用一个二维manifold 来表示（蓝色灰色组成的面）

流形学习认为我们所能观察到的数据实际上是由一个低维流形映射到高维空间上的。由于数据内部特征的限制，一些高维中的数据会产生维度上的冗余，实际上只需要比较低的维度就能唯一地表示。

选取了BERTvocab.txt中所有的词汇表，选取某个token$t_i$，利用encoder表示出其在数据集中所有出现的实例的embedding（上下文不同其）记为$\Phi \left(t_i\right)=\left\{{\varphi }_1\left(t_i\right),{\varphi }_2\left(t_i\right),\dots \right\}$。通过计算inter-type和intra-type的余弦距离计算簇类间距离和对于token $t_i$而言的簇类内距离和：
$$S_{\text{inter }}\triangleq {\mathbb{E}}_{i\ne j}\left[\cos \left(\varphi \left(t_i\right),\varphi \left(t_j\right)\right)\right]$$
其中$\varphi (t_i)$ 是$\Phi (t_i)$中的一个随机向量，$\varphi (t_j)$ 是$\Phi (t_j)$中的一个随机向量。

$$S_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}}\triangleq {\mathbb{E}}_i\left[{\mathbb{E}}_{k\ne l}\left[\cos \left({\varphi }_k\left(t_i\right),{\varphi }_l\left(t_i\right)\right)\right]\right]$$
在最外面取了平均，所以衡量的是token $t_i$而言的簇类内距离。

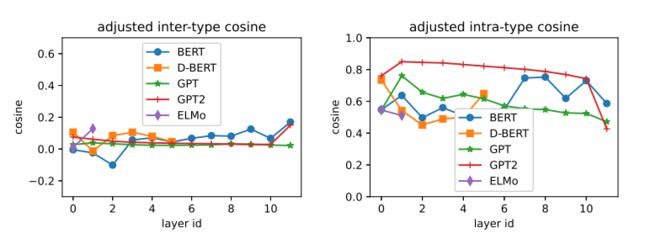
针对主流的embedding模型进行分析：

layer越深，簇类间距离越高，特别是GPT2的最后一层，相对更具有各向异性。S_intra指数一般都很高，说明任意向量都有很高的余弦相似度，不同类型的嵌入在更深的层次上越来越接近，而相同类型的实例的嵌入却在扩散。除了GPT-2，最后一层layer的余弦距离都相对较小。

2. Clusters

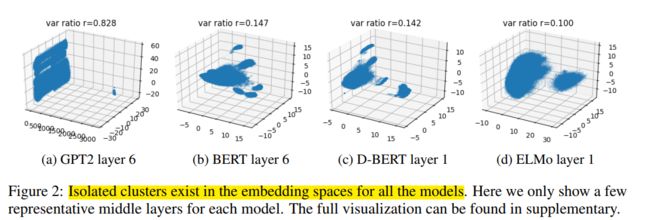
对每一layer的embedding都进行降维，并计算PCA的方差贡献率，计算大于0.8最少需要的层数。

所有模型的嵌入空间中都存在孤立的聚类。

GPT2的第2层到第10层中表现出双岛特性，在最后一层合并成一个大集群。在所有PTM所有层上都能观察到类似的集群行为。

通过Silhouette Method计算聚类个数$|C|$，通过Maximum Mean-Silhouette(MMS) score计算衡量各个簇类在向量空间中是如何分布的，MMS越大说明簇类间距离分隔越大，越小说明簇类越重叠。Figure3可以看到GPT2模型有更明显的集群效应。

其后论文探究了中心化（shift mean to the origin）后的向量分布情景，即在聚好的簇中，将原始的向量距离计算减去簇类内的平均向量，类似于中心化。即：
$$S_{\text{inter }}^{\prime }\triangleq {\mathbb{E}}_c\left[{\mathbb{E}}_{i\ne j}\left[\cos \left({\bar{\varphi }}^c\left(t_i\right),{\bar{\varphi }}^c\left(t_j\right)\right)\right]\right],\text{ where }{\bar{\varphi }}^c(t)={\varphi }^c(t)-{\mathbb{E}}_{{\varphi }^c}\left[{\varphi }^c(t)\right]$$

$$S_{\text{intra }}^{\prime }\triangleq {\mathbb{E}}_c\left[{\mathbb{E}}_i\left[{\mathbb{E}}_{k\ne l}\left[\cos \left({\bar{\varphi }}_k^c\left(t_i\right),{\bar{\varphi }}_l^c\left(t_i\right)\right)\right]\right]\right]$$

• 图1说明中心化后的每一个layer的簇类间余弦距离都趋向于0，说明簇类间的空间具备各向同性；
• 而簇类内的向量相似度呈现总体下降趋势，表明同一类型/单词的多个实例正在各个layer上缓慢扩散。

3. 低维流形

3.1 GPT是瑞士卷流形

BERT和D-BERT向量倾向于沿着更多维度分布，而GPT和GPT2在向量空间中倾向于将tokens嵌入低维流形中。更具体地说，我们发现大多数tokens都嵌入在螺旋带中，螺旋随着层数加深而变厚，形成瑞士卷形状的表面。

3.2 tokens在空间中的变化

为了验证GPT族的流形结构，通常认为越相关的单词距离理应当越近。在Bert和GPT的tokens embedding 中选定符号组\ & ·以及单词组the first man六个使用的比较频繁的单词进行标注，可以看到BERT的向量能够使得相似的单词在欧式距离上成簇状靠的更近，GPT的更像螺旋带分布。

3.3 词频

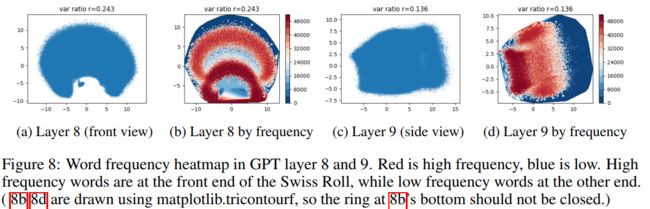
论文还发现所有模型都试图将高频率的单词映射到向量空间中的某个特定区域，而不是将它们分散到整个空间。

较深的红色表示高词频向量分布相对集中，且更倾向于分布在瑞士卷流形的前端；蓝色表示低词频向量分布，分布在瑞士卷的最末端。当模型发现了生僻词时，把他添加到流形的最末端。

3.4 LID

虽然原始空间维数为768，但我们观测到的流形具有更低的固有维数，这意味着流形上的数据点移动的自由度更小。例如，在3-D空间的瑞士卷上，任何点都只能有2-d自由度，因此内在维数只有2。我们采用LID相对于参考点局部估计维数。LID由Houle(2013)提出，最近被用于深度学习模型表征。根据Amsaleg et al. (2015) 给出的LID的近似KNN估计方法：$\widetilde{LID}(p)=-{\left(\frac{1}{K}{\sum }_{i=1}^K\log \frac{\mathrm{dist}\left(p,q_i\right)}{{\max }_i\left(\mathrm{dist}\left(p,q_i\right)\right)}\right)}^{-1}$.

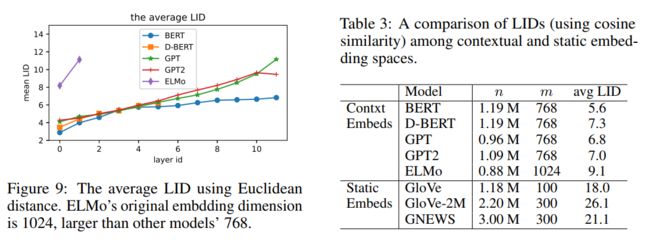
LID越大，manifold structrue越分散，一言以蔽之，可以理解为LID是原本的高维数据保留信息所能降低到的最低维度数目。

在所有上下文嵌入层中，LID值都有明显的增加趋势。在图9中，我们还可以看到层数和LID之间的近似线性关系。**随着layer越来越深，流形逐渐扩散化并慢慢失去聚合力，导致数据样本扩散，如图4所示类型内余弦随深度而减小。**随着层的深入，每个token向量都通过添加它们的向量(并连接非线性转换)从上下文收集信息。这可以解释局部子空间的扩展，因此LID在更深层次上增加。表3可以看到静态向量间的LID普遍高于上下文向量空间，意味着数据点在静态嵌入中更加各向同性，这可能是因为它们的词汇表$V$很大。

这段话我们就更深入的理解LID，就是衡量高维模型表征能力的指标；

LID越大，manifold structrue越分散，样本逐渐扩散化，向量分布更容易具有各向同性，更不容易是个convex cone，得到的cosine距离越不容易相似，分数越不容易高。

4. 启示

1. 词频在向量分布中起着关键作用，如何利用好词频信息？
2. 簇类内各向同性，全局视角来看各向异性的结论，是否是说明在进行句子匹配任务时先聚类找到对应的簇类去，再计算cos相似度会好一些。考虑聚类的作用。

Isotropic Contextual Word Representation in BERT

Paper Url.

Paper Url. Github Url. 《A Cluster-based Approach for Improving Isotropy in Contextual Embedding Space》. Accepted @ ACL 2021 short paper.

Abstract

表征学习的最新进展表明，各向同性(即单位方差和不相关)嵌入可以显著提高下游任务的性能，收敛速度更快，泛化效果更好。在这个项目中，我们提出了一个算法，既适用于预训练阶段，也适用于微调阶段。我们的算法试图使表示各向同性。我们分析了BERT模型在预训练和微调阶段的各向同性。实验结果表明，该算法能有效地提高预训练表示法的各向同性。但在微调阶段，我们不能提高模型的性能。

1. Isotropy度量

$Z(c)={\sum }_{w\in \mathcal{V}}\exp \left(c^{\top }v(w)\right)$，Z©应该近似为任意单位向量c的常数，$v(w)$是词汇表中词向量。

各向同性度量可以用$I(\{v(w)\})=\frac{{\min }_{\Vert c\Vert =1}Z(c)}{{\max }_{\Vert c\Vert =1}Z(c)}$来表示（具体推导可以参考Mu et al. 2018）。越趋向于1表示越各向同性。我们将C向量近似为$V^{T}V$的特征向量的集合，其中V是词表示的向量空间。

2. Algorithm

1. 先将文本表示进行用K-means时时聚类，一个簇类内是相似的文本表示
2. 分别计算每个簇类内的均值向量$\mu$
3. 中心化，减掉mean vector
4. 计算PCA向量
5. 减掉前D维最重要的信息。（最主导的方向对其他向量有很强的影响，从零均值单词向量中减去了主导方向的影响，将单词嵌入向弱方向）

后四步全都参考于Mu et al. 2018。

后面这一步$\tilde{v}(w)-{\sum }_{i=1}^D(u_i^{T}v(w))u_i$其实就是ZCA白化。

3. 实验结果

任务也都是在语义相似度匹配和分类务上进行都有所提高。

PCA后成球形，也即白化，whitening or sphering。

Learning to Remove: Towards Isotropic Pre-trained BERT Embedding

Paper Url. Github Url.

Accepted by ICANN2021

Abstract

词汇表征研究表明，各向同性嵌入可以显著提高下游任务的表现。然而，我们测量和分析了预先训练的BERT嵌入的几何形状，发现它远不是各向同性的。我们发现词向量不是以原点为中心，两个随机词之间的平均余弦相似度远高于零，这表明词向量分布在一个狭窄的锥体中，降低了词嵌入的表示能力。我们提出了一种简单而有效的方法来解决这个问题:用一组可学习权值去除BERT嵌入的几个主导方向。我们训练了单词相似度任务的权重，并表明处理后的嵌入更具各向同性。我们的方法在三个标准化任务上进行评价:词相似度、词类比和语义文本相似度。在所有任务中，我们的方法处理的词嵌入都优于原始的嵌入(词类比平均提高13%，语义文本相似度平均提高16%)和两种基线方法。该方法对超参数的变化具有较好的鲁棒性。

1. Contributions

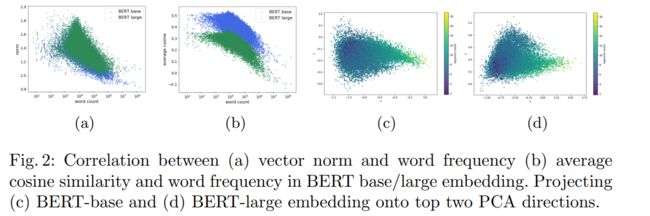
1. 测量、可视化和分析发现BERT向量是各向异性的，词向量的范数/平均余弦相似度与词的频率有很强的相关性。
2. 提出一种加权去除方法，学习去除主导方向。该方法的关键是利用一组经过训练的词相似度任务的可学习权值来决定去除方向的比例。
3. 我们在三个任务上评估我们的方法:单词相似度，单词类比和语义文本相似度。将该方法与BERT、ABTT方法和概念否定方法三种baseline进行性能比较。

2. Observation

平均余弦相似度远高于零，这意味着词向量不是均匀分布在向量空间中，而是分布在一个狭窄的圆锥体中

我们发现第一个PCA系数对单词频率进行显著地编码，二者具有很高的Pearson相关性(约为−0.7)。频率高的词接近原点(范数更小)，分布相对均匀(平均余弦相似度更低)，频率低的词被挤压成一个更窄的锥体，被推离原点。这可能导致两个明显不同的词，但其对应的词向量在欧几里得空间中可能产生高度的相似度，从而影响下游任务的性能。
在BERT的预训练过程中，最终对应于mask tokens的隐藏向量被输入到词汇表的softmax输出中。直觉理解，在训练过程中，对于任何给定的文本的hidden state，相应掩码词的表示向量将被推向隐藏状态的方向，优化目标是去得到更大的似然值，而其他所有词的嵌入则会被推向隐藏状态的负方向，得到更小的似然值。频率越低的词越会被推向各种隐藏状态的负方向。因此，低频率的单词被压缩到一个更窄的圆锥体中。

对于任何一个token$w_i$，其损失函数可以分为两部分:一块$A_{w_i}$为训练语料中context中不包含token $w_i$的部分，一块$B_{w_i}$为包含 $w_i$的部分。设$P(\text{Context}\in A_{w_i})$和$P(\text{Context}\in B_{w_i})$表示A和B块上下文的概率，$L_{A_{w_i}}(w_i)$和$L_{B_{w_i}}(w_i)$分别为A/B块的loss。因此token$w_i$的损失函数可以定义为：
$$L_{w_i}=P\left(\text{ context }\in A_{w_i}\right)L_{A_{w_i}}\left(w_i\right)+P\left(\text{ context }\in B_{w_i}\right)L_{B_{w_i}}\left(w_i\right)$$

3. Method

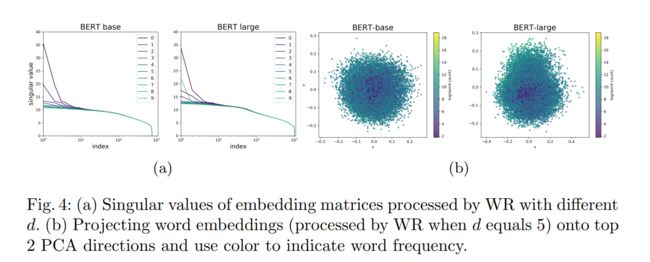
重点就是如何去除dominant principle components. 不是直接去除或者减掉，学习一个权重序列哪几个应当减掉的更多。

4. Experiments

进行Weight Removal操作之后词频也是球化，词频高低的中心化，高的反而容易边缘化分布。