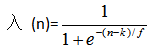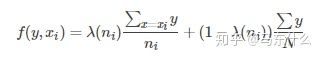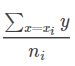pytorch标签onehot编码_特征编码方法总结—part1

最近又碰到了高基数类别特征的处理问题，正好也要把相关的解决方案添加到现有的线上机器学习系统里，这里总结一下以后免得又忘记了。

在特征工程里，特征编码是占比很重的一块，在kaggle的结构化数据比赛中，最终帮助选手胜利的关键因素之一往往是高级特征的构造和特征编码（很多时候特征编码也是在构造高级的特征），下面就来总结一下吧。

1、labelencoder 标签编码

如果是无序的非数值离散特征，一般直接用onehot独热编码了，有序的非数值离散特征才会用到标签编码，因为大部分算法是没有内置自动识别类别特征的功能的，所以需要做这么一步简单的转换，原理很easy了不用废话了，为了文章看起来完整才写的，使用labelencoder或者自己用字典来做映射即可。

2、onehotencoder 独热编码

针对类别特征，例如【男人，女人】，【晴天，雨天，阴天】，类别型特征，无序，最简单快捷的方式是通过独热编码转化为【0，1】或者【0，0，1】这样的形式，模型才能识别，同时也起到了扩充特征的作用（例如逻辑在特征进行onehot展开之后表达能力一般能够得到较好的提高）。sklearn的onehot，pandas的get_dummies或者自己用字典映射均可。

• 优点：独热编码解决了分类器不好处理属性数据的问题，在一定程度上也起到了扩充特征的作用。它的值只有0和1，不同的类型存储在垂直的空间。
• 缺点：1、当类别的数量很多时，特征空间会变得非常大。2、对于特定任务，例如词向量化，直接使用onehot的方式是无法考虑到词之间的交互关系的，onehot之后损失了部分信息。推而广之，如果特征之间是非独立的（比如上下文的词之间是存在交互关系，时间序列数据之间存在某些内在关系），就不能简单的使用onehot功能

3、label_binarize 二值化编码

举个例子就知道是干嘛用的了，比如特征为【晴天，雨天，阴天，雷暴】则特征转化为【是否晴天，是否雨天，是否阴天，是否雷暴】，用数字来表示【雷暴】就是[0,0,0,1]，和onthot看起来很类似，很多时候不那么严格界定，其实等同于onehot，一般来说独热编码的结果是多个0和1个1组成的比如类别特征的处理，但是也存在处理之后出现多个1和多个0的情况，比如文本问题，whatever，不做严格区分，因为很多文章都不划分那么细，反正自己心里有数就行了，实现使用sklearn的label_binarize或者自己用字典来实现。

4、直方图编码与计数编码(count)

直方图编码，主要针对类别型特征与类别型标签的一种编码方式，还是举个例子来说明什么是直方图编码吧，最好理解了：

假设类别特征f1=【A，A，B，B，B，C，C】，对应的二分类标签为【0，1，0，1，1，0，0】，则我们是这样来计算类别特征f1中对应的类别的编码值的：

以A为例，类别特征f1的值为A的样本有两个，这两个样本的标签分别为【0，1】，则A被直方图编码为【1/2,1/2】=【0.5，0.5】（A的样本一共有2个所以分母为2，其中一个样本标签为1，一个样本标签为0），实际上就是计算取值为A的样本中，不同类别样本的比例，然后用这个比例来替换原始的类别标签，这里需要强调的是，无论是直方图编码还是我们后面要介绍的target encoding，本质上都是用类别特征的统计量来代替原来的类别值的，没什么神秘的地方，很好理解。

如法炮制，我们来对B进行类别编码，f1值为B的一共3个样本，其中一个样本标签为0，两个样本标签为1，所以B被编码为【1/3,2/3】，很好理解了。同样对于C，一共两个样本，并且两个样本标签均为0，则编码为【2/2,0】。

直方图编码实际上存在着比较多的问题，我们目前针对高基类特征的常用的目标编码或者均值编码实际上可以看作是在直方图编码之上的问题改进。

直方图编码存在以下问题：

1、没有考虑到类别特征中不同类别的数量的影响，举个例子，假设样本的某个类别特征为【A,A,A,A,A,A,B】，对应的标签为【0，0，0，1，1，1，0】，则根据直方图编码的公式得到的结果为A：【1/2,1/2】，B：【1,0】，然而这实际上对于A来说是很不公平的，因为B的样本数量太少，计算出来的结果根本不能算是明显的统计特征，而很可能是一种噪音，这实际上是一种非常“过拟合”的计算方式，因为一旦测试集中的样本有多个B之后，B的直方图编码的结果很可能发生非常大的变化；

2、假设没有1中出现的情况，所有的类别A，B的数量都比较均匀，直方图编码还是存在着一个潜在的隐患，直方图编码的计算非常依赖于训练集中的样本标签的分布情况，以f1特征的那个例子为例，实际上直方图这么计算的隐含的假设是潜在的所有的数据的在类别f1上的每一个类别计算出来的结果可以用训练集的结果来近似代替，简单说比如我在训练集中算出来A的直方图编码为【1/2,1/2】，即类别为A的样本中有一半标签0的样本，一半标签1的样本，那么一旦测试集的分布情况发生改变，或者是训练集本身的采样过程就是有偏的，则直方图编码的结果就是完全错误的，（比如全样本中，类别为A的样本其实只有10%是标签为0的，90%标签为1的，则这个时候A的直方图编码为【1/10,9/10】，训练集的产生可能是有偏的）；

所以在可用的资料和kaggle比赛中很少有人会用到直方图编码，更多的使用target encoding和mean encoding。下面是简单的直方图编码的实现，因为不怎么用就懒得优化了。

def histogram_encoding(X,y):
    category=list(set(X))
    labels=list(set(y))
    data=pd.concat([X,pd.DataFrame(y)],axis=1)
    data.columns=['data','labels']
    dictionary={}
    for item in category:
        temp=data[data['data']==item]
        tp=temp['labels'].value_counts()
        if tp.shape[0]

而计数编码就更加简单了，以二分类问题为例，就是根据每一个类别特征的类别对二分类标签进行sum求和得到每个类别中样本标签为1的总数，一行搞定,不知道为什么这么简单的编码方式在比赛中效果这么好。。。：

df.groupby(['category'])['target'].transform(sum)

5、WOE编码

实际上这里细心一点就可以发现，woe编码仅仅针对于二分类问题，woe编码如下：

原理很简单就是根据woe的公式来计算即可。实际上woe编码的方法很容易就可以扩展到多类，后面会写。

单纯从woe的公式就可以看出woe编码存在的问题：

1、分母可能为0的问题；

2、类似于直方图编码，没有考虑到不同类别数量的大小，例如类别特征为【A，A，A，A，A，A，B】而标签为【0，0，0，1，1，1，1】这样的情况计算出来的woe明显对A这个类别不公平

3、应用局限性太大了，只能针对二分类问题，并且特征也必须为离散特征。

4、训练集计算的woe编码结果可能和测试集计算的woe编码结果存在较大差异（所有基于统计特征的编码方式的通病）

首先我们调个包，使用到的是注明scikit-learn contrib分支中的category_encoders：

from category_encoders import *
import pandas as pd
from sklearn.datasets import load_boston
bunch = load_boston()
y = bunch.target > 22.5
X = pd.DataFrame(bunch.data, columns=bunch.feature_names)
enc = WOEEncoder(cols=['CHAS', 'RAD']).fit(X, y)
numeric_dataset = enc.transform(X)

通过查看内部核心实现代码，对比原始公式：

https://github.com/scikit-learn-contrib/categorical-encoding/blob/master/category_encoders/woe.py 源代码地址太多了自己看

源代码中大致实现了上图的计算逻辑，为了避免除0的问题，引入了“regulation”这个参数（用户自定义，默认为1）来进行拉普拉斯平滑。

核心代码：

           nominator = (stats['sum'] + self.regularization) / (self._sum + 2*self.regularization)
           denominator = ((stats['count'] - stats['sum']) + self.regularization) / (self._count - self._sum + 2*self.regularization)

所以对于很小样本的数据进行woe编码计算的结果会和实际计算上有出入，不过说实话如果样本数量很小个人认为没有太多编码的必要吧，统计学意义非常不明显。

这里我们只解决了上面除0的问题，对于问题二，我们可以使用IV值的思路，针对类别特征中不同类别的数量给woe的公式施加一个惩罚项：

这样就把样本数量的问题也考虑进去了。实现也很简单，计算出woe编码结果之后再计算惩罚项然后相乘即可，不赘述了。

针对问题3，如果要拓展多多分类，我想到的思路是使用直方图编码的思路：

这是原始的woe编码公式，修改的思路是，分子为类别特征中第i个类别中的 y_i/y_sum，分母为所有训练样本中的yi/y_sum，举个例子把，例如类别特征为【A，A，A，B，B】，标签为【0，0，1，2，1】，则对于A，类别0的编码的计算过程为ln(2/3 / 2/5)依次类推，不过就是不知道这种编码结果效果好不好，下次打比赛的时候试试看好了。

针对问题4，没想出来什么好的办法

6、target encoding 目标编码

先调一波包

from category_encoders import *
import pandas as pd
from sklearn.datasets import load_boston
bunch = load_boston()
y = bunch.target
X = pd.DataFrame(bunch.data, columns=bunch.feature_names)
enc = TargetEncoder(cols=['CHAS', 'RAD']).fit(X, y)
numeric_dataset = enc.transform(X)
print(numeric_dataset.info())

原理也不难；

分类问题

对于C分类问题,目标编码（target encode）后只需要增加C−1个属性列,如果C远远小于N,则相对one-hot-encoding可以节省很多内存. 其出发点是用概率P(y=yi|x=xi)代替属性值x, 其中x表示属性值,y表示类别值. 但实际问题中,经常会遇到x=xi对应的样本数目比较少,导致对P(y=yi|x=xi)的计算不准确. 所以后来的改进结果是引入先验概率P(y=yi),公式转换成 ：

细心一点就可以发现，如果上述不引入先验概率P以及lambda项，其实就是我们前面提到的直方图编码。直方图编码是target encode和mean encode的前辈了。

其中j∈[0,C),ni是训练集中xi的样本个数,λ(ni)∈[0,1]负责计算两个概率值的可靠性,针对应用有不同的定义方法,如下是一个例子 ：

(我们的category_encoders库使用的就是上面这个例子的计算方式，其中参数k和f分别是我们的min_sample_leaf和smoothing参数),二者都是一个可调参数,当x在训练集中出现次数n=k时,λ(n)=0.5,两个概率的可靠性相等,随者n的增大,先验概率P(y=yi)的可靠性逐渐降低.

我第一次接触这里的入(n)还是比较奇怪的，长得很奇怪，不过其实带几个数进去算一算也能理解这个项的意义了，公式转换成这样主要是考虑到有的类别xi的数量太少从而编码结果不精确（原因在直方图编码那边已经描述过了），对于数量很大的xi来说，入(n)的引入几乎没有影响，比如n=100000，此时入(n)的计算结果趋近于1，先验项的系数趋近于0，则target_encode计算的结果和直方图编码的计算结果是基本近似的。如果n很小，比如n=2，则入(n)=0.731，此时根据先验项的系数为0.269，即最终编码结果部分受到先验项的影响，从而通过这种方式降低由于n数量太小而导致的编码不精确的问题（这尼玛也行。。。类似于用先验的统计值对原来的编码结果进行一个调和加权平均），所以显然，这里的k越大，则意味着先验的影响越大。

回归问题

回归问题同样可以使用均值编码,只需要把概率换成均值

其中

表示x=xi对应的y均值,

是整个训练集上y的均值

我们来看一看源代码：

下面是核心实现代码：

    def fit_target_encoding(self, X, y):
        mapping = {}

        for switch in self.ordinal_encoder.category_mapping:
            col = switch.get('col')
            values = switch.get('mapping')

            prior = self._mean = y.mean()

            stats = y.groupby(X[col]).agg(['count', 'mean'])

            smoove = 1 / (1 + np.exp(-(stats['count'] - self.min_samples_leaf) / self.smoothing))
            smoothing = prior * (1 - smoove) + stats['mean'] * smoove
            smoothing[stats['count'] == 1] = prior

            if self.handle_unknown == 'return_nan':
                smoothing.loc[-1] = np.nan
            elif self.handle_unknown == 'value':
                smoothing.loc[-1] = prior

            if self.handle_missing == 'return_nan':
                smoothing.loc[values.loc[np.nan]] = np.nan
            elif self.handle_missing == 'value':
                smoothing.loc[-2] = prior

            mapping[col] = smoothing

        return mapping

核心中的核心代码：

            prior = self._mean = y.mean() ##计算连续值标签的均值

            stats = y.groupby(X[col]).agg(['count', 'mean']) #根据类别特征中的不同的类分别进行groupby，聚合函数为计数group和
#求平均值mean

            smoove = 1 / (1 + np.exp(-(stats['count'] - self.min_samples_leaf) / self.smoothing))
#计算smoove值，
            smoothing = prior * (1 - smoove) + stats['mean'] * smoove#计算最终的编码结果smoothing值
            smoothing[stats['count'] == 1] = prior#出现次数为1的类别直接用先验值prior代替

为了便于理解还是举个例子吧。

假设特征f1为【A，A，A，B，B，C，C，C，C，D】，对应的连续值标签为【1，2，3，4，5，6，7，8，9，10】则根据上面的源代码我们计算结果如下：

对于A，对应的子数据集为【A，A，A】。【1，2，3】，则y.mean()=(1+2+3+4+。。。+10)/10=5.5，groupby之后的结果为count=3，mean=（1+2+3）/3=2，因为min_samples_leaf和smoothing默认值为1，则smoove=1/(1+np.exp(-3-min_samples_leaf))=0.982

5.5*(1-0.892)+2*0.892=2.378，调包试了一下，结果差不多，思路没什么问题。

target encode是针对高基数类别特征进行处理手段的最好的选择之一。但它也有缺点，就是容易过拟合，因为所有的统计计算都是基于训练集来的，所以一旦新数据集的分布发生变化，就会产生类似于过拟合所产生的不良的训练效果，所以接下来我们要介绍target encode 的升级版，也是目前最常用的特征编码方法之一，mean encoding。

7、mean encoding 均值编码

网上有实现的源码，就不费心思去看论文了，直接根据代码来解释均值编码的原理吧，均值编码的原理和target encoding非常非常类似，只不过为了避免过拟合加入了一些特别的手段而已。

首先来看一下初始化的部分：

self.categorical_features 用来指定特征变量中的类别变量的变量名;

self.n_splits 用与指定后面交叉验证的折数（后文详述）

self.learned_stats 用于统计量的存放

然后做了一个分类和回归的判断，分类和回归下的均值编码略有不同

判断是否存在先验权重计算函数，没有的话则默认使用下面的公式并且k和f是根据用户给定的字典类型的参数取值的，有的话则使用用户给定的先验权重计算函数来计算先验权重：

如果用户没有提供先验权重计算函数也没有提供k和f的参数值则k，f则使用默认值分别为k=2，f=1

然后我们看一下“fit_transform”部分：

首先是copy一个新的特征矩阵Xnew，然后根据分类还是回归问题选择不同的抽样方式（分层抽样or普通抽样），然后我们生成一个字典learned_stas用于存放编码之后的结果类似这样：

接下来是核心实现的部分：

            for variable, target in product(self.categorical_features, self.target_values):
                nf_name = '{}_pred_{}'.format(variable, target)
                X_new.loc[:, nf_name] = np.nan
                for large_ind, small_ind in skf.split(y, y):
                    nf_large, nf_small, prior, col_avg_y = MeanEncoder.mean_encode_subroutine(
                        X_new.iloc[large_ind], y.iloc[large_ind], X_new.iloc[small_ind], variable, target, self.prior_weight_func)
                    X_new.iloc[small_ind, -1] = nf_small
                    self.learned_stats[nf_name].append((prior, col_avg_y))

X_new中通过loc函数先占个坑，然后进入交叉验证：（补充：建议原始的输入变量X和y先shuffle一下再进入计算）

然后我们就进入了核心的实现 MeanEncoder.mean_encode_subroutine（静态函数）：

    @staticmethod
    def mean_encode_subroutine(X_train, y_train, X_test, variable, target, prior_weight_func):
        X_train = X_train[[variable]].copy()
        X_test = X_test[[variable]].copy()
 
        if target is not None:
            nf_name = '{}_pred_{}'.format(variable, target)
            X_train['pred_temp'] = (y_train == target).astype(int)  # classification
        else:
            nf_name = '{}_pred'.format(variable)
            X_train['pred_temp'] = y_train  # regression
        prior = X_train['pred_temp'].mean()
 
        col_avg_y = X_train.groupby(by=variable, axis=0)['pred_temp'].agg({'mean': 'mean', 'beta': 'size'})
        col_avg_y['beta'] = prior_weight_func(col_avg_y['beta'])
        col_avg_y[nf_name] = col_avg_y['beta'] * prior + (1 - col_avg_y['beta']) * col_avg_y['mean']
        col_avg_y.drop(['beta', 'mean'], axis=1, inplace=True)
 
        nf_train = X_train.join(col_avg_y, on=variable)[nf_name].values
        nf_test = X_test.join(col_avg_y, on=variable).fillna(prior, inplace=False)[nf_name].values
 
        return nf_train, nf_test, prior, col_avg_y

还是举个例子好理解吧，假设这里categorical_features=['f1','f2','f3'],target=[0,1,2]，那么这里我们以variable=‘f1’，target=0为

例来计算，首先是去原始数据中标签为0的样本的f1特征：

 X_train['pred_temp'] = (y_train == target).astype(int)

然后是根据X_train['pred_temp']的来计算target为0的样本的占比情况以作为prior先验概率的值。

prior = X_train['pred_temp'].mean()

然后接下来的计算方式和target encoding是一致的：

        col_avg_y = X_train.groupby(by=variable, axis=0)['pred_temp'].agg({'mean': 'mean', 'beta': 'size'})
        col_avg_y['beta'] = prior_weight_func(col_avg_y['beta'])
        col_avg_y[nf_name] = col_avg_y['beta'] * prior + (1 - col_avg_y['beta']) * col_avg_y['mean']
        col_avg_y.drop(['beta', 'mean'], axis=1, inplace=True)

唯一不同的方式是，mean encoding这里用到了交叉计算的方式，以5折交叉为例，在80%的数据上计算编码结果得到转换的规则，

然后将剩下20%的数据按照转换规则进行转换，最后将结果返回：

        nf_train = X_train.join(col_avg_y, on=variable)[nf_name].values
        nf_test = X_test.join(col_avg_y, on=variable).fillna(prior, inplace=False)[nf_name].values
 
        return nf_train, nf_test, prior, col_avg_y

最后：

X_new.iloc[small_ind, -1] = nf_small

把测试集的转换结果赋给原始数据的copy。

综上所属，mean encoding的原理和target encoding基本是一样的，只不过比target encoding多了一个交叉计算的步骤，假设有10000条数据，

target encoding是直接在这10000条数据上进行编码结果的计算的，而mean encoding则是每次用类似与模型训练的方法，比如五折交叉计算，用

80%的数据计算编码结果然后赋给剩下的20%，重复5次则所有特征都编码完毕，这样的好处就是一定程度上降低过拟合的影响。

完整代码如下，回归的原理类似公式如下，自己看吧：（注意，输入X，y都必须是pandas格式的否则会报错）

import numpy as np
import pandas as pd
from sklearn.model_selection import StratifiedKFold,KFold
from itertools import product
 
class MeanEncoder:
    def __init__(self, categorical_features, n_splits=5, target_type='classification', prior_weight_func=None):
        """
        :param categorical_features: list of str, the name of the categorical columns to encode
 
        :param n_splits: the number of splits used in mean encoding
 
        :param target_type: str, 'regression' or 'classification'
 
        :param prior_weight_func:
        a function that takes in the number of observations, and outputs prior weight
        when a dict is passed, the default exponential decay function will be used:
        k: the number of observations needed for the posterior to be weighted equally as the prior
        f: larger f --> smaller slope
        """
 
        self.categorical_features = categorical_features
        self.n_splits = n_splits
        self.learned_stats = {}
 
        if target_type == 'classification':
            self.target_type = target_type
            self.target_values = []
        else:
            self.target_type = 'regression'
            self.target_values = None
 
        if isinstance(prior_weight_func, dict):
            self.prior_weight_func = eval('lambda x: 1 / (1 + np.exp((x - k) / f))', dict(prior_weight_func, np=np))
        elif callable(prior_weight_func):
            self.prior_weight_func = prior_weight_func
        else:
            self.prior_weight_func = lambda x: 1 / (1 + np.exp((x - 2) / 1))

                    
    @staticmethod
    def mean_encode_subroutine(X_train, y_train, X_test, variable, target, prior_weight_func):
        X_train = X_train[[variable]].copy()
        X_test = X_test[[variable]].copy()
 
        if target is not None:
            nf_name = '{}_pred_{}'.format(variable, target)
            X_train['pred_temp'] = (y_train == target).astype(int)  # classification
        else:
            nf_name = '{}_pred'.format(variable)
            X_train['pred_temp'] = y_train  # regression
        prior = X_train['pred_temp'].mean()
 
        col_avg_y = X_train.groupby(by=variable, axis=0)['pred_temp'].agg({'mean': 'mean', 'beta': 'size'})
        col_avg_y['beta'] = prior_weight_func(col_avg_y['beta'])
        col_avg_y[nf_name] = col_avg_y['beta'] * prior + (1 - col_avg_y['beta']) * col_avg_y['mean']
        col_avg_y.drop(['beta', 'mean'], axis=1, inplace=True)
 
        nf_train = X_train.join(col_avg_y, on=variable)[nf_name].values
        nf_test = X_test.join(col_avg_y, on=variable).fillna(prior, inplace=False)[nf_name].values
 
        return nf_train, nf_test, prior, col_avg_y
 
    def fit_transform(self, X, y): 
        
        """
        :param X: pandas DataFrame, n_samples * n_features
        :param y: pandas Series or numpy array, n_samples
        :return X_new: the transformed pandas DataFrame containing mean-encoded categorical features
        """
        X_new = X.copy()
        if self.target_type == 'classification':
            skf = StratifiedKFold(self.n_splits)
        else:
            skf = KFold(self.n_splits)
 
        if self.target_type == 'classification':
            self.target_values = sorted(set(y))
            self.learned_stats = {'{}_pred_{}'.format(variable, target): [] for variable, target in
                                  product(self.categorical_features, self.target_values)}
            for variable, target in product(self.categorical_features, self.target_values):
                nf_name = '{}_pred_{}'.format(variable, target)
                X_new.loc[:, nf_name] = np.nan
                for large_ind, small_ind in skf.split(y, y):
                    nf_large, nf_small, prior, col_avg_y = MeanEncoder.mean_encode_subroutine(
                        X_new.iloc[large_ind], y.iloc[large_ind], X_new.iloc[small_ind], variable, target, self.prior_weight_func)
                    X_new.iloc[small_ind, -1] = nf_small
                    self.learned_stats[nf_name].append((prior, col_avg_y))
        else:
            self.learned_stats = {'{}_pred'.format(variable): [] for variable in self.categorical_features}
            for variable in self.categorical_features:
                nf_name = '{}_pred'.format(variable)
                X_new.loc[:, nf_name] = np.nan
                for large_ind, small_ind in skf.split(y, y):
                    nf_large, nf_small, prior, col_avg_y = MeanEncoder.mean_encode_subroutine(
                        X_new.iloc[large_ind], y.iloc[large_ind], X_new.iloc[small_ind], variable, None, self.prior_weight_func)
                    X_new.iloc[small_ind, -1] = nf_small
                    self.learned_stats[nf_name].append((prior, col_avg_y))
        return X_new
 
    def transform(self, X):
        """
        :param X: pandas DataFrame, n_samples * n_features
        :return X_new: the transformed pandas DataFrame containing mean-encoded categorical features
        """
        X_new = X.copy()
 
        if self.target_type == 'classification':
            for variable, target in product(self.categorical_features, self.target_values):
                nf_name = '{}_pred_{}'.format(variable, target)
                X_new[nf_name] = 0
                for prior, col_avg_y in self.learned_stats[nf_name]:
                    X_new[nf_name] += X_new[[variable]].join(col_avg_y, on=variable).fillna(prior, inplace=False)[
                        nf_name]
                X_new[nf_name] /= self.n_splits
        else:
            for variable in self.categorical_features:
                nf_name = '{}_pred'.format(variable)
                X_new[nf_name] = 0
                for prior, col_avg_y in self.learned_stats[nf_name]:
                    X_new[nf_name] += X_new[[variable]].join(col_avg_y, on=variable).fillna(prior, inplace=False)[
                        nf_name]
                X_new[nf_name] /= self.n_splits
 
        return X_new

实际上均值编码的思路挺好，但凡是涉及到标签的编码方式多少都会有信息泄漏的问题，并且如果训练集和测试集的标签分布很不均衡，有监督编码很容易称为罪魁祸首。解决的办法就是交叉验证，之前打比赛写的用交叉验证来获得woe编码和target编码的结果：

def mean_woe_target_encoder(train,test,target,col,n_splits=10):
    folds = StratifiedKFold(n_splits)

    y_oof = np.zeros(train.shape[0])
    y_oof_2= np.zeros(train.shape[0])
    y_test_oof = np.zeros(test.shape[0]).reshape(-1,1)
    y_test_oof2 = np.zeros(test.shape[0]).reshape(-1,1)

    splits = folds.split(train, target)
    
    for fold_n, (train_index, valid_index) in enumerate(splits):
        X_train, X_valid = train[col].iloc[train_index], train[col].iloc[valid_index]
        y_train, y_valid = target.iloc[train_index], target.iloc[valid_index]
        clf=ce.target_encoder.TargetEncoder()
    
    #    dtrain = lgb.Dataset(X_train, label=y_train)
    #    dvalid = lgb.Dataset(X_valid, label=y_valid)
    
        #clf = lgb.train(params, dtrain, 10000, valid_sets = [dtrain, dvalid], verbose_eval=1, early_stopping_rounds=500)
        clf.fit(X_train.values,y_train.values)    
        y_pred_valid = clf.transform(X_valid.values)
        y_oof[valid_index] = y_pred_valid.values.reshape(1,-1)

        tp=(clf.transform(test[col].values)/(n_splits*1.0)).values
        tp=tp.reshape(-1,1)
        y_test_oof+=tp    
    
        del X_train, X_valid, y_train, y_valid
        gc.collect()    
        
    for fold_n, (train_index, valid_index) in enumerate(splits):
        X_train, X_valid = train[col].iloc[train_index], train[col].iloc[valid_index]
        y_train, y_valid = target.iloc[train_index], target.iloc[valid_index]
        clf=ce.woe.WOEEncoder()
    
    #    dtrain = lgb.Dataset(X_train, label=y_train)
    #    dvalid = lgb.Dataset(X_valid, label=y_valid)
    
        #clf = lgb.train(params, dtrain, 10000, valid_sets = [dtrain, dvalid], verbose_eval=1, early_stopping_rounds=500)
        clf.fit(X_train.values,y_train.values)    
        y_pred_valid = clf.transform(X_valid.values)
        y_oof2[valid_index] = y_pred_valid.values.reshape(1,-1)
    
        tp=(clf.transform(test[col].values)/(n_splits*1.0)).values
        tp=tp.reshape(-1,1)
        y_test_oof2+=tp    
        del X_train, X_valid, y_train, y_valid
        gc.collect()     
    return y_oof,y_oof_2,y_test_oof,y_test_oof2