【20211214】【信号处理】使用Matlab求解信号的频谱图、幅度谱、相位谱
一、背景知识
1. 频谱
信号的频谱由两部分组成:幅度谱和相位谱。
2. 幅度谱
在傅里叶分析中,把各个分量的幅度随频率的变化称为信号的幅度谱。
补充幅度谱的求解方法:
(1)如果不是直流分量的频率,即 f≠0Hz,则幅度谱 = 频谱幅度 / (N/2) ;
(2)对于直流分量,即 f=0Hz,则幅度谱 = 频谱幅度 / N ;
(参考:如何决定要使用多少点来做fft)
(参考:【数字信号处理】Matlab做fft时点数N怎么选取)
3. 相位谱
在傅里叶分析中,把各个分量的相位随频率的变化称为信号的相位谱。
(参考:频谱、幅度谱、功率谱和能量谱)
(参考:信号与系统--幅度谱和相位谱)
二、举个栗子~
%
clear; clc; close all; warning off;
fs = 1000; % 采样频率
t = 0 : 1/fs : 10;
datalength = length(t);
s1 = 10 * sin(2 * pi * 50 * t); % 信号1
s2 = 3 * sin(2 * pi * 100 * t); % 信号2
s3 = 15 * cos(2 * pi * 30 * t); % 信号3
s4 = 1 * randn(1, datalength); % 信号4(高斯白噪声)
s = s1 + s2 + s3 + s4; % 合成信号
% FFT
N = 1024; % FFT点数
sFFT = fft(s, N); % N点傅里叶变换
sFFTPow = abs(sFFT) .^ 2; % 功率(功率信号的傅里叶变换是功率谱)
sFFTPowdB = pow2db(sFFTPow(1:N/2)); % 功率转db
% 原始信号波形和频谱图
figure;
sp1 = subplot(3, 1, 1);
plot(s1, 'linewidth', 1.5); hold on;
plot(s2, 'linewidth', 1.5); hold on;
plot(s3, 'linewidth', 1.5); hold on;
plot(s4, 'linewidth', 1.5); hold off;
legend('s1', 's2', 's3', 's4');
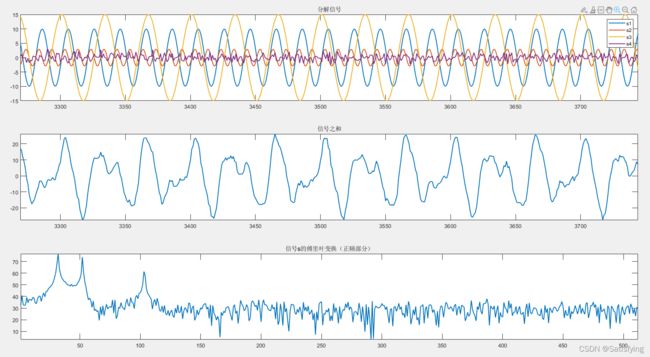
title('分解信号'); axis('tight');
sp2 = subplot(3, 1, 2);
plot(s, 'linewidth', 1.5);
title('合成信号'); axis('tight');
sp3 = subplot(3, 1, 3);
plot(sFFTPowdB, 'linewidth', 1.5);
title('信号s的傅里叶变换(只画正频部分)'); axis('tight');
linkaxes([sp1, sp2], 'x');
% 幅度谱和相位谱
magnitude = abs(sFFT); % 幅度谱
phase = angle(sFFT); % 相位谱(rad)
figure;
sp1 = subplot(2, 1, 1);
plot(magnitude, 'linewidth', 1.5);
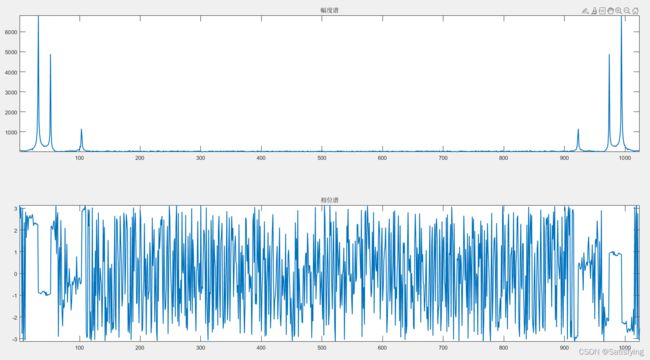
title('幅度谱'); axis('tight');
sp2 = subplot(2, 1, 2);
plot(phase, 'linewidth', 1.5);
title('相位谱'); axis('tight');
linkaxes([sp1, sp2], 'x');运行结果:
将图一局部放大:
观察运行结果注意到:幅度谱有三个尖峰,对应于傅里叶变换之前的三个单频正弦信号,但幅度谱的三个幅值均不等于傅里叶变换之前的信号幅值。
但除以傅里叶变换点数 N 之后的幅度谱三个尖峰幅值 = 原信号幅值的一半(这一点我还不是特别明白为什么要除以 N,为什么为原信号幅值的一半,有可能得到的是双边谱,如果只显示正频部分,乘以 2 之后就和原信号幅值一致了~)(解释见上面补充的幅度谱求解方法),相位谱也可以由 rad 转为 °,代码如下:
% 幅度谱和相位谱
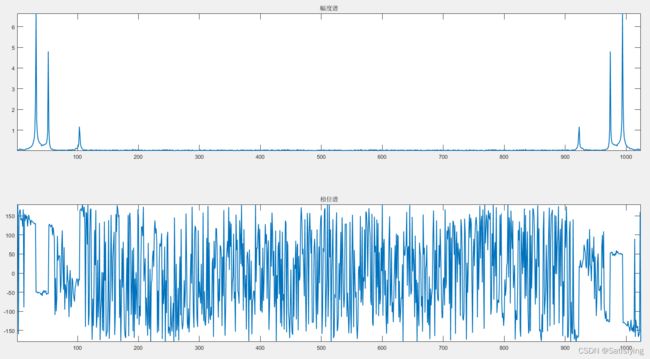
magnitude = abs(sFFT) ./ N; % 幅度谱
phase = angle(sFFT) * 180 / pi; % 相位谱(rad)(参考:如何得到信号的幅度谱和相位谱)
(参考:matlab 数字滤波入门)
运行结果如下图:
(参考:使用python(scipy和numpy)实现快速傅里叶变换(FFT)最详细教程)
(参考:傅里叶变换通俗解释及快速傅里叶变换的python实现)
(参考:[已解决] 关于傅里叶变换与相位谱、幅值谱的问题)
(参考:如何获得信号的相位fft&——我能在时域中得到相位吗?)
三、知识点
1. 能量信号和功率信号
(1)能量有限,功率为零的信号为能量信号;(例如单一脉冲信号、单一方波等)
(2)能量无限,功率有限的信号为功率信号;(例如无限延伸的正弦信号、无限延伸的高斯白噪声,所以本文中的合成信号 s 为功率信号,其频谱为功率谱)
所有周期信号都是功率信号(因为能量无限),所有有限数量的脉冲信号都是能量信号(因为能量有限)。
(参考:能量信号和功率信号的分别)
(参考:图像的频率谱和功率谱代表什么_频谱、能量谱、功率谱的区别与联系)
2. Matlab 中 angle 和 phase 的区别
angle 和 phase 处理单个标量数据时没有任何差别,都是用 atan是函数求相位。但是对于向量和矩阵,angle 函数是对每个数据独立求相位角度,而 phase 会对输出结果做判断,如果相邻两个输出角度之差的绝对值超过 3.5,那么 phase 函数会对其重新处理,保证输出的相邻两个相位角度差值的绝对值不会超过 3.5。(有点类似于相位解缠绕的意思~)
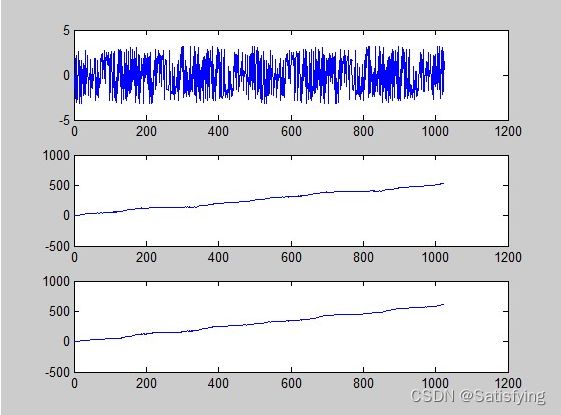
下图从上到下,是网上某例 angle, phase, unwrap 函数的运行结果对比,可以看出 phase 和 unwrap 的效果特别相似!
(参考:[已答复] phase函数和angle函数有什么区别?)
(参考:matlab中angle和phase的区别)