语义分割 评价指标(global_acc, mean_acc, mean_iou)等numpy实现

语义分割常见评价指标global_acc, mean_acc, mean_iou计算，个人学习记录，仅供参考。

一、理论计算

假设真实标签为:

预测标签为：

则手动列出混淆矩阵可得：

1.1 全局准确率

预测正确的像素数量 / 总的像素数量
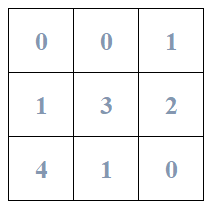
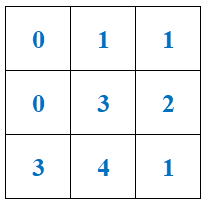
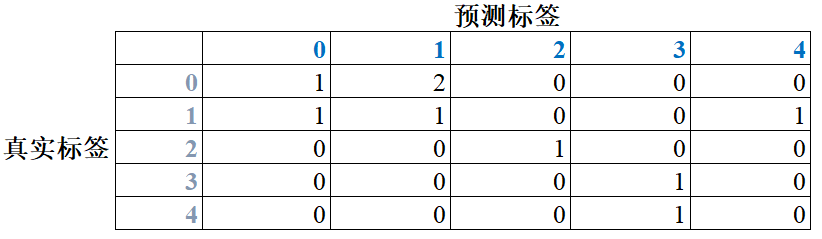
global_acc = (1+1+1+1+0) / 9 = 4 / 9 = 0.4444，即混淆矩阵对角线元素之和除以混淆矩阵所有元素和。

1.2 平均准确率

分别算出每一类的准确率，分子为对角线元素，分母为真实标签i数量，这里具体为第i行的元素和。
cls_0_acc = 1 / (1+2) = 1/3;
cls_1_acc = 1 / (1+1+1) = 1/3;
cls_2_acc = 1 / 1 = 1;
cls_3_acc = 1 / 1 = 1;
cls_4_acc = 0 / 1 = 0;
mean_acc = (1/3 + 1/3 + 1 + 1 + 0) / 5 = 8/15 = 0.5333

1.3 平均iou

分别计算出每一类的iou，再求平均。
cls_0_iou = 1 / (3 + 2 - 1) = 1/4;
cls_1_iou = 1 / (3 + 3 - 1) = 1/5;
cls_2_iou = 1 / (1 + 1 - 1) = 1;
cls_3_iou = 1 / (1 + 2 - 1) = 1/2;
cls4_iou = 0 / (1 + 1 - 0) = 0;
mean_iou = (1/4 + 1/5 +1 + 1/2 + 0) / 5 = 0.39

参考链接：
语义分割前言
基于pytorch的FCN网络简单实现

二、代码实现

2.1 计算混淆矩阵

计算真实标签与预测标签的混淆矩阵，先贴出代码再详细分析过程。

def _fast_hist(label_true, label_pred, n_class):
    # 根据真实标签和预测标签计算混淆矩阵
    mask = (label_true >= 0) & (label_true < n_class)
    hist = np.bincount(
        n_class * label_true[mask].astype(int) +
        label_pred[mask], minlength= n_class**2).reshape(n_class, n_class)
    return hist

详细分析：

import numpy as np
true_l = np.array([[0,0,1],
                   [1,3,2],
                   [4,1,0]])

pred_l = np.array([[0,1,1],
                   [0,3,2],
                   [3,4,1]])

def _fast_hist(label_true, label_pred, n_class):

    # mask在元素值大于等于0，小于等于n_class的地方填True
    mask = (label_true >= 0) & (label_true < n_class)
    print('mask:\n', mask)

    # label_true[mask]用mask中为true的索引取label_true
    print('label_true[mask]:\n', label_true[mask].astype(int))

    # 以下个人理解为相当于编码过程,label_true看成'十位',label_pred看成'个位'
    # 将5*5的矩阵与0-24的地址对应上
    print('n_class * label_true[mask]:\n', n_class * label_true[mask].astype(int))
    print('label_pred[mask]:\n', label_pred[mask])

    print('n_class * label_true[mask].astype(int) + label_pred[mask]:\n',
          n_class * label_true[mask].astype(int) + label_pred[mask])

    hist = np.bincount(
        n_class * label_true[mask].astype(int) +
        label_pred[mask], minlength= n_class**2).reshape(n_class, n_class)

    print('hist:\n', hist)
    
    return hist

_fast_hist(label_true=true_l, label_pred=pred_l, n_class=5)

输出结果：

mask:
 [[ True  True  True]
 [ True  True  True]
 [ True  True  True]]
label_true[mask]:
 [0 0 1 1 3 2 4 1 0]
n_class * label_true[mask]:
 [ 0  0  5  5 15 10 20  5  0]
label_pred[mask]:
 [0 1 1 0 3 2 3 4 1]
n_class * label_true[mask].astype(int) + label_pred[mask]:
 [ 0  1  6  5 18 12 23  9  1]
hist:
 [[1 2 0 0 0]
 [1 1 0 0 1]
 [0 0 1 0 0]
 [0 0 0 1 0]
 [0 0 0 1 0]]

其中np.bincount()输出不同元素出现的次数，注意参数minlength的作用，参考链接：
np.bincount()用法介绍
numpy.bincount详解

2.2 根据混淆矩阵计算各指标

def label_accuracy_score(label_trues, label_preds, n_class):

    hist = np.zeros((n_class, n_class))

    # 一个batch里可能有多个数据，通过迭代器逐个计算
    for lt, lp in zip(label_trues, label_preds):
        hist += _fast_hist(lt.flatten(), lp.flatten(), n_class)  # 其实这里也可以不flatten, 函数值arr[mask]这一步也可帮忙拉平

    print('hist:\n', hist)

    acc = np.diag(hist).sum() / hist.sum()  # 混淆矩阵对角线元素和 / 所有元素和
    acc_cls = np.diag(hist) / hist.sum(axis=1)  # hist.sum(axis=1) => [3,3,1,1,1],对应每一类真实标签数量
    acc_cls = np.nanmean(acc_cls)

    iu = np.diag(hist) / (hist.sum(axis=1) + hist.sum(axis=0) - np.diag(hist))
    mean_iu = np.nanmean(iu)  # hist.sum(axis=0) => [2,3,1,2,1],对应每一类预测标签数量

    freq = hist.sum(axis=1) / hist.sum()
    fwavacc = (freq[freq > 0] * iu[freq > 0]).sum()  # 没弄懂是什么意思

    return acc, acc_cls, mean_iu, fwavacc

print('======计算指标======')
acc, acc_cls, mean_iu, fwavacc = label_accuracy_score(label_trues=true_l, label_preds=pred_l, n_class=5)
print('global_acc', acc)
print('mean_acc:', acc_cls)
print('mean_iou:', mean_iu)
print('fwavacc', fwavacc)

输出结果：

======计算指标======
hist:
 [[1. 2. 0. 0. 0.]
 [1. 1. 0. 0. 1.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 1. 0.]
 [0. 0. 0. 1. 0.]]
global_acc 0.4444444444444444
mean_acc: 0.5333333333333333
mean_iou: 0.39
fwavacc 0.31666666666666665

Tips：
1.np.diag()返回矩阵对角元素
2.np.nanmean()，计算时忽略nan，参考链接:
np.nansum()、np.nanmean() 函数用法