朴素贝叶斯模型
朴素贝叶斯模型
朴素贝叶斯方法是在贝叶斯算法基础上进行了相应的简化,即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重,也没有哪个属性变量对于决策结果占有着较小的比重。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果,但是在实际的应用场景中,极大地简化了贝叶斯方法的复杂性。
数学基础公式总结
先验概率 P ( A ) P(A) P(A):在不考虑任何情况下,A事件发生的概率。
条件概率 P ( B ∣ A ) P(B|A) P(B∣A): A事件发生情况下,B事件发生的概率。
后验概率 P ( A ∣ B ) P(A|B) P(A∣B): 在B事件发生之后,对A事件进行评估。
P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B) = \frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB)
全概率:如果 A A A和 A ‘ A^` A‘构成样本空间的一个划分,那么事件 B B B的概率为: A A A和 A ‘ A^` A‘ 的概率分别乘以 B B B对这两个事件的概率之和。

基于条件概率的贝叶斯定律数学公式:
P ( A ∣ B ) = P ( A ) ∗ P ( B ∣ A ) P ( B ) = P ( A ) ∗ P ( B ∣ A ) ∑ i = 1 n P ( B ∣ A i ) ∗ P ( A i ) P(A|B) = \frac{P(A)*P(B|A)}{P(B)} = \frac{P(A)*P(B|A)}{\sum^n_{i = 1}P(B|A_i)*P(A_i)} P(A∣B)=P(B)P(A)∗P(B∣A)=∑i=1nP(B∣Ai)∗P(Ai)P(A)∗P(B∣A)
算法原理
朴素贝叶斯基于特征之间是独立的,这一朴素假设,应用贝叶斯定律的监督学习算法:
对应给定样本x的特征向量 x 1 , x 2 , . . . x m x_1,x_2,...x_m x1,x2,...xm,该样本X的类别y可以由贝叶斯公式得到:
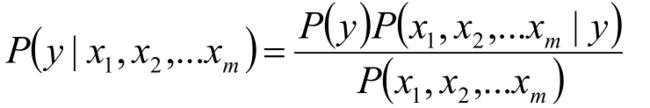
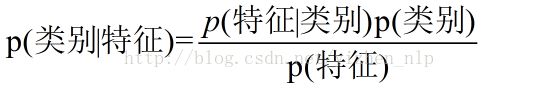
推导过程如下:
公式优化得到:

在给定样本情况下, P ( x 1 , x 2 , . . . x m ) P(x_1,x_2,...x_m) P(x1,x2,...xm)是常数,所以得到:

算法流程
朴素贝叶斯流程定义如下:
- 设x={a 1 ,a 2 ,…,a m }为待分类项,其中a为x的一个特征属性
类别集合为C={y 1 ,y 2 ,…,y n }
分别计算P(y 1 |x), P(y 2 |x),…,P(y n |x)的值(贝叶斯公式)
如果P(y k |x)=max{ P(y 1 |x),P(y 2 |x),…,P(y n |x) },那么认为x为y k 类型
朴素贝叶斯方法三种常见模型
高斯朴素贝叶斯
Gaussian Naive Bayes是指当特征属性为连续值时,而且分布服从高斯分布,那么在计算 P ( x ∣ y ) P(x|y) P(x∣y)的时候可以直接使用高斯分布的概率公式:
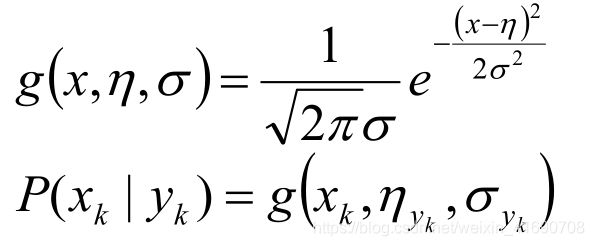
因此只需要计算出各个类别中此特征项划分的各个均值和标准差
其中CkCk为Y的第k类类别。μkμk 和σ2kσk2为需要从训练集估计的值。GaussianNB会根据训练集求出μkμk 和σ2kσk2。μkμk 为在样本类别CkCk中,所有XjXj(j=1,2,3…j=1,2,3…)的平均值。σ2kσk2为在样本类别CkCk中,所有XjXj(j=1,2,3…j=1,2,3…)的方差。
在使用GaussianNB的fit方法拟合数据后,我们可以进行预测。此时预测有三种方法,包括predict,predict_log_proba和predict_proba。
predict方法就是我们最常用的预测方法,直接给出测试集的预测类别输出。
predict_proba则不同,它会给出测试集样本在各个类别上预测的概率。容易理解,predict_proba预测出的各个类别概率里的最大值对应的类别,也就是predict方法得到类别。
predict_log_proba和predict_proba类似,它会给出测试集样本在各个类别上预测的概率的一个对数转化。转化后predict_log_proba预测出的各个类别对数概率里的最大值对应的类别,也就是predict方法得到类别。
伯努利朴素贝叶斯
Bernoulli Naive Bayes是指当特征属性为连续值时,而且分布服从伯努利分布,那么在计算 P ( x ∣ y ) P(x|y) P(x∣y)的时候可以直接使用伯努利分布的概率公式:
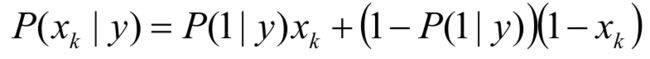
伯努利分布是一种离散分布,只有两种可能的结果。1表示成功,出现的概率为p;0表示失败,出现的概率为 q = 1 − p q=1-p q=1−p;其中均值为 E ( x ) = p E(x)=p E(x)=p,方差为 V a r ( X ) = p ( 1 − p ) Var(X)=p(1-p) Var(X)=p(1−p)
多项朴素贝叶斯
Multinomial Naive Bayes是指当特征属性服从多项分布,从而,对于每个类别y,参数为θ y =(θ y1 ,θ y2 ,…,θ yn ),其中n为特征属性数目,那么P(x i |y)的概率为。
多项式分布:把二项扩展为多项就得到了多项分布。比如扔骰子,不同于扔硬币,骰子有6个面对应6个不同的点数,这样单次每个点数朝上的概率都是1/6(对应p1~p6,它们的值不一定都是1/6,只要和为1且互斥即可,比如一个形状不规则的骰子),重复扔n次,如果问有x次都是点数6朝上的概率就是: 。更一般性的问题会问:“点数16的出现次数分别为(x1,x2,x3,x4,x5,x6)时的概率是多少?其中sum(x1x6)= n”。这就是一个多项式分布问题。这时只需用上边公式思想累乘约减就会得到下面图1的概率公式。
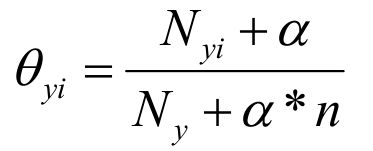
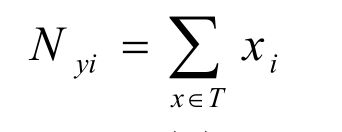

sklearn实现,
#利用提取的word counts特征来fitNaive Bayes
clf = MultinomialNB()
clf.fit(xtrain_ctv, ytrain)
predictions = clf.predict_proba(xvalid_ctv)
print ("logloss: %0.3f " % multiclass_logloss(yvalid, predictions))
代码解析
除了MultinomialNB之外,还有GaussianNB就是先验为高斯分布的朴素贝叶斯,BernoulliNB就是先验为伯努利分布的朴素贝叶斯。
class sklearn.naive_bayes.MultinomialNB(alpha=1.0,
fit_prior=True,
class_prior=None)
MultinomialNB假设特征的先验概率为多项式分布,即如下式:


参数
- alpha: 浮点型可选参数,默认为1.0,其实就是添加拉普拉斯平滑,即为上述公式中的λ ,如果这个参数设置为0,就是不添加平滑
- fit_prior: 布尔型可选参数,默认为True,布尔参数fit_prior表示是否要考虑先验概率,如果是false,则所有的样本类别输出都有相同的类别先验概率。否则可以自己用第三个参数class_prior输入先验概率,或者不输入第三个参数class_prior,让MultinomialNB自己从训练集样本来计算先验概率,
此时的先验概率为 P ( Y = C k ) = m k m 0 P(Y = C_k) = \frac{m_k}{m_0} P(Y=Ck)=m0mk
其中m为训练集样本总数量, m k m_k mk为输出第k类别的训练集样本数。 - class_prior: 可选参数,默认为None。

还有其他参数:

>>> import numpy as np
>>> X = np.random.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.fit(X, y)
MultinomialNB()
>>> print(clf.predict(X[2:3]))
[3]
全部将其搞透彻,研究彻底,学会拿来即用都行啦的样子与打算。
学习心得
会自己推广朴素贝叶斯公式,将其应用到训练模型和生成数据集当中。
会自己将各种的贝叶斯算法给其搞清楚,全部将其搞定都行啦的理由与打算,
各种贝叶斯公式都给其搞透彻,研究彻底!
用到那个算法再去理解那个算法中的机理与其研究方法。
