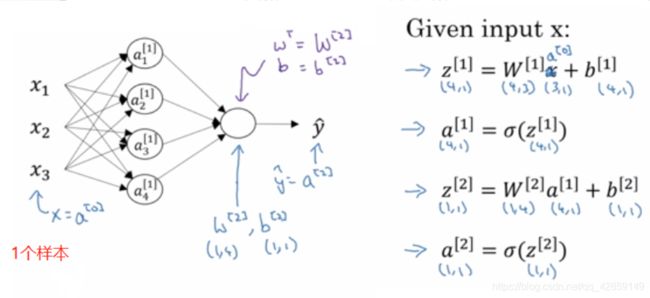
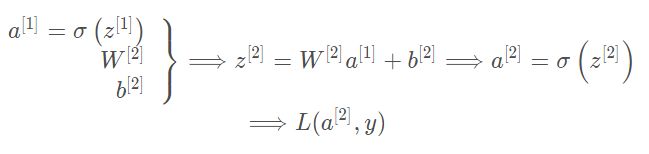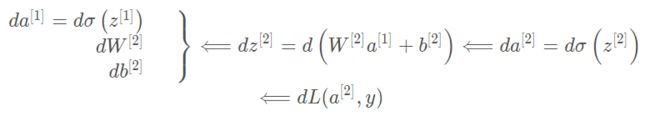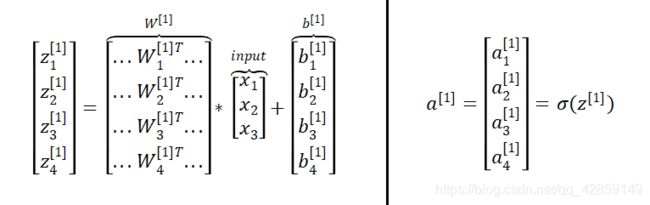- 深度学习-130-RAG技术之基于Anything LLM搭建本地私人知识库的应用策略问题总结(一)
皮皮冰燃
深度学习深度学习人工智能RAG
文章目录1AnythingLLM的本地知识库1.1本地知识库应用场景1.2效果对比及思考1.3本地体现在哪些方面1.3.1知识在本地1.3.2分割后的文档在本地1.3.3大模型部署运行在本地2问错问题带来的问题2.1常见的问题2.2原因分析3为什么LLM不使用我的文件?3.1LLM不是万能的【omnipotent】3.2LLM不会自省【introspect】3.3AnythingLLM是如何工作的
- 3DMAX点云算法:实现毫米级BIM模型偏差检测(附完整代码)
夏末之花
人工智能
摘要本文基于激光雷达点云数据与BIM模型的高精度对齐技术,提出一种融合动态体素化与多模态特征匹配的偏差检测方法。通过点云预处理、语义分割、模型配准及差异分析,最终实现建筑构件毫米级偏差的可视化检测。文中提供关键代码实现,涵盖点云处理、特征提取与深度学习模型搭建。一、核心算法流程点云预处理与特征增强去噪与下采样:采用统计滤波与体素网格下采样,去除离群点并降低数据量。语义分割:基于PointNet++
- 数据增强:扩充数据集,提升模型的鲁棒性
AI天才研究院
DeepSeekR1&大数据AI人工智能大模型LLM大模型落地实战指南计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
数据增强:扩充数据集,提升模型的鲁棒性1.背景介绍1.1数据集的重要性在机器学习和深度学习领域中,数据集是训练模型的基础。高质量的数据集对于构建准确、鲁棒的模型至关重要。然而,在现实世界中,获取大量高质量的数据通常是一个巨大的挑战。数据采集过程耗时耗力,而且成本高昂。此外,某些领域的数据存在隐私和安全问题,难以获取。1.2数据集不足的挑战当数据集规模有限时,模型很容易过拟合,无法很好地推广到新的、
- Docker打包深度学习项目
FLY_LTL
docker深度学习容器
文章目录Docker打包深度学习项目1.Docker和NVIDIAContainerToolkit的安装1.Docker2.NVIDIAContainerToolkit3.添加国内镜像源2.使用Dockerfile打包并保存镜像1.Dockerfile2.通过Dockerfile生成镜像3.保存镜像和加载4.运行Docker并测试参考Docker打包深度学习项目本文来源于个人实践总结,供各位同学参
- 深度革命:ResNet 如何用 “残差连接“ 颠覆深度学习
安意诚Matrix
机器学习笔记深度学习人工智能
一文快速了解ResNet创新点在深度学习的历史长河中,2015年或许是最具突破性的一年。这一年,微软亚洲研究院的何恺明团队带着名为ResNet(残差网络)的模型横空出世,在ImageNet图像分类竞赛中以3.57%的错误率夺冠,将人类视觉的识别误差(约5.1%)远远甩在身后。更令人震撼的是,ResNet将神经网络的深度推至152层,彻底打破了"深层网络无法训练"的魔咒。这场革命的核心,正是一个简单
- 智能形状匹配技术全解析:从经典算法到深度学习与神经形态计算【超级详细版】
AI筑梦师
计算机视觉算法深度学习人工智能机器学习计算机视觉python
智能形状匹配技术全解析:从经典算法到深度学习与神经形态计算1.引言1.1研究背景在计算机视觉、模式识别、医学影像分析和自动驾驶等领域,形状匹配是核心任务之一。然而,现实世界的形状往往存在可变性(Variability),主要体现在以下几个方面:形变(Deformation):物体可能由于柔性材料、外力作用或生物运动发生非刚性形变。尺度变化(ScaleVariation):目标形状在不同场景下可能大
- Python 模拟鼠标轨迹算法
a485240
鼠标轨迹计算机外设
一.鼠标轨迹模拟简介传统的鼠标轨迹模拟依赖于简单的数学模型,如直线或曲线路径。然而,这种方法难以捕捉到人类操作的复杂性和多样性。AI大模型的出现,使得能够通过深度学习技术,学习并模拟更自然的鼠标移动行为。二.鼠标轨迹算法实现AI大模型通过学习大量的人类鼠标操作数据,能够识别和模拟出自然且具有个体差异的鼠标轨迹。以下是实现这一技术的关键步骤:数据收集:收集不同玩家在各种游戏环境中的鼠标操作数据,包括
- 什么是机器视觉3D引导大模型
视觉人机器视觉
机器视觉3D3d数码相机机器人人工智能大数据
机器视觉3D引导大模型是结合深度学习、多模态数据融合与三维感知技术的智能化解决方案,旨在提升工业自动化、医疗、物流等领域的操作精度与效率。以下从技术架构、行业应用、挑战与未来趋势等方面综合分析:一、技术架构与核心原理多模态数据融合与深度学习3D视觉引导大模型通常整合RGB图像、点云数据、深度信息等多模态输入,通过深度学习算法(如卷积神经网络、Transformer)进行特征提取与融合。例如,油田机
- 深度学习在医学影像分析中的应用:DeepSeek系统的实践与探索
Evaporator Core
#深度学习#DeepSeek快速入门DeepSeek进阶开发与应用深度学习人工智能
随着人工智能技术的迅猛发展,深度学习在医学领域的应用逐渐成为研究热点。医学影像分析作为医疗诊断的重要组成部分,正受益于深度学习技术的突破。DeepSeek系统是一种基于深度学习的医学影像分析平台,旨在通过高效、精准的算法辅助医生进行疾病诊断和治疗决策。本文将深入探讨DeepSeek系统的技术原理、实现方法及其在医学影像分析中的实际应用,并结合代码示例展示其核心功能。1.DeepSeek系统的技术架
- 【深度学习遥感分割|论文解读2】UNetFormer:一种类UNet的Transformer,用于高效的遥感城市场景图像语义分割
985小水博一枚呀
论文解读深度学习transformer人工智能网络cnn
【深度学习遥感分割|论文解读2】UNetFormer:一种类UNet的Transformer,用于高效的遥感城市场景图像语义分割【深度学习遥感分割|论文解读2】UNetFormer:一种类UNet的Transformer,用于高效的遥感城市场景图像语义分割文章目录【深度学习遥感分割|论文解读2】UNetFormer:一种类UNet的Transformer,用于高效的遥感城市场景图像语义分割2.Re
- PyTorch 深度学习博客
Zoro|
PyTorchDeepLearning人工智能
PyTorch深度学习博客欢迎来到我的PyTorch深度学习博客!在这里,我将分享使用PyTorch学习和实践深度学习项目的点滴经验。本博客适用于初学者和有一定基础的开发者,旨在帮助大家快速搭建环境、掌握核心概念,并通过实例了解实际应用。环境配置为了确保项目的稳定性和兼容性,我选择了Python3.9环境,并在conda创建的虚拟环境中运行最新且稳定的PyTorch版本2.6.0。1.创建Pyth
- 深度学习五大模型:CNN、Transformer、BERT、RNN、GAN详细解析
深度学习
卷积神经网络(ConvolutionalNeuralNetwork,CNN)原理:CNN主要由卷积层、池化层和全连接层组成。卷积层通过卷积核在输入数据上进行卷积运算,提取局部特征;池化层则对特征图进行下采样,降低特征维度,同时保留主要特征;全连接层将特征图展开为一维向量,并进行分类或回归计算。CNN利用卷积操作实现局部连接和权重共享,能够自动学习数据中的空间特征。适用场景:广泛应用于图像处理相关的
- 算力技术创新驱动多场景应用演进
智能计算研究中心
其他
内容概要算力技术创新正成为数字经济时代的基础性驱动力,从异构计算架构的多元融合到量子计算的颠覆性突破,技术演进不断突破物理与算法的双重边界。在工业互联网场景中,边缘计算通过分布式节点实现毫秒级响应,支撑智能制造产线的实时控制;智能安防系统依托深度学习模型与流计算技术,完成海量视频数据的动态解析;而科学计算领域通过分布式计算与模型压缩技术,将基因测序、气候模拟等复杂任务的效率提升至新量级。值得注意的
- AI模型技术前沿与跨场景应用实践
智能计算研究中心
其他
内容概要当前AI模型技术正呈现多维度突破与跨领域融合的特征。从技术演进角度看,可解释性模型与量子计算框架的协同发展正在突破传统黑箱限制,而联邦学习、自适应优化等技术则为复杂场景建模提供了新的方法论支撑。应用层面,TensorFlow与PyTorch框架在医疗影像诊断、金融时序预测等领域的实战案例,验证了深度学习模型在垂直行业的泛化能力。值得关注的是,工具链整合已成为技术落地的关键环节,MXNet与
- 融合AMD与NVIDIA GPU集群的MLOps:异构计算环境中的分布式训练架构实践
在深度学习的背景下,NVIDIA的CUDA与AMD的ROCm框架缺乏有效的互操作性,导致基础设施资源利用率显著降低。随着模型规模不断扩大而预算约束日益严格,2-3年更换一次GPU的传统方式已不具可持续性。但是Pytorch的最近几次的更新可以有效利用异构计算集群,实现对所有可用GPU资源的充分调度,不受制于供应商限制。本文将深入探讨如何混合AMD/NVIDIAGPU集群以支持PyTorch分布式训
- 深度学习框架PyTorch——从入门到精通(4)数据转换
Fansv587
Torch框架学习深度学习pytorch人工智能python经验分享
转换(Transforms)很多时候,数据并不总是以训练机器学习算法所需的最终处理形式出现。所以我们需要使用变换对数据进行一些处理,使其适合训练。所有TorchVision数据集都有两个参数——transform来修改特征,target_transform来修改标签——接受包含转换逻辑的可调用项。torchvision.transform模块提供了几个开箱即用的转换。FashionMNIST数据集
- 深度学习框架PyTorch——从入门到精通(5)构建神经网络
Fansv587
Torch框架学习深度学习pytorch神经网络经验分享
构建神经网络获取训练设备定义类模型层nn.Flattennn.Linearnn.ReLUnn.Sequentialnn.Softmax模型参数补充说明argmax神经网络是由一些层或者模块组成的,这些层和模块会对数据进行各种操作。在PyTorch里,torch.nn这个命名空间提供了你搭建自己神经网络所需要的所有基础组件。PyTorch里的每一个模块都是nn.Module类的子类。一个神经网络本身
- 深度学习框架PyTorch——从入门到精通(5)自动微分
Fansv587
深度学习pytorch人工智能
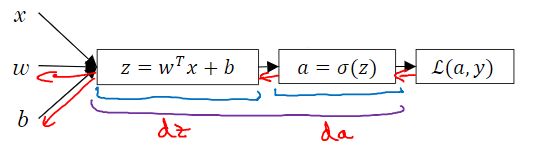
使用torch.autograd自动微分张量、函数和计算图计算梯度禁用梯度追踪关于计算图的更多信息张量梯度和雅可比乘积在训练神经网络时,最常用的算法是反向传播。在该算法中,参数(模型权重)根据损失函数的梯度相对于给定参数进行调整。为了计算这些梯度,PyTorch有一个内置的微分引擎,名为torch.autograd。它支持为任何计算图自动计算梯度。考虑最简单的一层神经网络,具有输入x、参数w和b以
- 消融实验(Ablation Study)
xwhking
深度学习机器学习深度学习消融实验
消融实验(AblationStudy)定义:消融实验是一种科学研究方法,通过逐步移除模型、算法或系统中的某个组件(如模块、层、特征、数据等),观察其对整体性能的影响,从而验证该组件的必要性和有效性。其名称来源于医学领域的“消融术”(切除部分组织以研究功能),在计算机视觉、机器学习和深度学习中被广泛用于分析模型设计。为什么要做消融实验?1.验证组件的有效性核心目的:确认模型中某个设计(如注意力机制、
- 数据集格式转换——json2txt、xml2txt、txt2json【复制就能用】
kay_545
YOLO11改进有效涨点python人工智能机器学习
秋招面试专栏推荐:深度学习算法工程师面试问题总结【百面算法工程师】——点击即可跳转本专栏所有程序均经过测试,可成功执行专栏地址:YOLO11入门+改进涨点——点击即可跳转欢迎订阅目录json2txt脚本xml2txttxt2json
- AI人工智能深度学习算法:在量子计算中的应用
AI天才研究院
AI大模型企业级应用开发实战AI大模型应用入门实战与进阶DeepSeekR1&大数据AI人工智能大模型计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
1.背景介绍随着科技的不断发展,人工智能和量子计算成为了当今世界的热门话题。人工智能的深度学习算法在处理大规模数据和复杂任务方面取得了显著的成果,而量子计算则具有强大的并行计算能力和高效的信息处理能力。将人工智能与量子计算相结合,为解决一些具有挑战性的问题提供了新的思路和方法。本文将探讨人工智能深度学习算法在量子计算中的应用,包括其背景、意义和应用场景。2.核心概念与联系在人工智能中,深度学习是一
- 还在为找图发愁?图生生AI以图生图,一键生成专属风格!
图生生
人工智能aiAI作画图生生
你是否也遇到过这样的烦恼:想为文章配图,却找不到风格合适的图片?设计海报时,灵感枯竭,不知从何下手?看到喜欢的图片风格,却无法应用到自己的作品中?别担心,图生生AI生图来帮你!只需上传一张图片,AI就能自动生成相似风格的图片,让你轻松拥有专属图库!图生生AI生图是一款基于人工智能技术的图片生成工具,它能够深度学习和理解图片的风格、色彩、构图等元素,并以此为基础生成全新的图片。无论你是设计师、自媒体
- 深度学习中的Channel,通道数是什么?
%KT%
深度学习深度学习人工智能
参考文章:直观理解深度学习的卷积操作,超赞!-CSDN博客如何理解卷积神经网络中的通道(channel)_神经网络通道数-CSDN博客深度学习-卷积神经网络—卷积操作详细介绍_深度卷积的作用-CSDN博客正文:在跑深度学习代码的过程中,经常遇到的一个报错是:模型尺寸不匹配的问题。一般pytorch中尺寸/张量的表现方式是:torch.size([16,3,24,24])。这四个参数的含义如下:16
- AI人工智能深度学习算法:搭建可拓展的深度学习模型架构
AI大模型应用之禅
DeepSeekR1&AI大模型与大数据javapythonjavascriptkotlingolang架构人工智能
深度学习、模型架构、可拓展性、神经网络、机器学习1.背景介绍深度学习作为人工智能领域最前沿的技术之一,在图像识别、自然语言处理、语音识别等领域取得了突破性的进展。深度学习模型的成功离不开其强大的学习能力和可拓展性。本文将深入探讨深度学习算法的原理、模型架构设计以及可拓展性的关键要素,并通过代码实例和实际应用场景,帮助读者理解如何搭建可拓展的深度学习模型架构。2.核心概念与联系深度学习的核心概念是人
- 远程调试Python脚本之ptvsd
工头阿乐
PyTorch深度学习python开发语言
深度学习文章目录深度学习前言前言有时候需要远程调试Python脚本,怎么办呢…以下这段代码用于远程调试Python脚本,特别是通过VisualStudioCode(VSCode)的远程调试功能。它会在指定的服务器IP和端口上等待调试器的连接。#检查是否提供了服务器IP和端口ifargs.server_ipandargs.server_port:#远程调试-参见https://code.visual
- yolo模型coco数据集详解
工头阿乐
深度学习YOLO
深度学习文章目录深度学习前言前言instances_train2017.json和instances_val2017.json文件均分为五大部分,这五部分对应的关键字分别为info、licenses、images、annotations、categories。{"info":info,"licenses":[license1,license2,license3,...],"images":[ima
- 机器学习之向量化
珠峰日记
AI理论与实践机器学习人工智能
文章目录向量化是什么为什么要向量化提升计算效率简化代码与增强可读性适配模型需求怎么做向量化数据预处理特征提取特征选择向量构建机器学习与深度学习中向量化的区别数据特征提取方式机器学习深度学习模型结构与复杂度机器学习深度学习计算资源需求机器学习深度学习数据规模适应性机器学习深度学习向量化是什么向量化是把数据转化为向量形式进行表示与处理的过程。在机器学习与深度学习的范畴内,现实中的各类数据,像文本、图像
- 聊聊Python都能做些什么
·零落·
Python入门到掌握python开发语言
文章目录一、Python简介二、Python都能做些什么1.Web开发2.数据分析和人工智能3.自动化运维和测试4.网络爬虫5.金融科技三、Python开源库都有哪些1.Web开发2.数据分析和科学计算3.机器学习和深度学习4.网络爬虫5.自动化和测试6.其他常用库四、相关链接一、Python简介Python是一种解释型、面向对象、动态数据类型的高级程序设计语言。它最初由GuidovanRossu
- NLP高频面试题(四)——BN和LN的区别与联系,为什么attention要用LN
Chaos_Wang_
NLP常见面试题自然语言处理人工智能
在深度学习模型中,Normalization是一种极为重要的技巧,BatchNormalization(BN)和LayerNormalization(LN)是其中最为常用的两种方法。然而,二者在实际应用中有着明显的区别与联系,尤其在Transformer的Attention机制中,LN有着独特的优势。一、BN与LN的核心区别与联系1.BatchNormalization(BN)BN的思想源于一个叫
- 理解深度学习1-简介
shangjg3
PyTorch深度学习实战深度学习人工智能
人工智能(AI)旨在打造模仿智能行为的系统。它覆盖了众多方法,涵盖了基于逻辑、搜索和概率推理的技术。机器学习是AI的一个分支,它通过对观测数据进行数学模型拟合来学习决策制定。这个领域近年来迅猛发展,现在几乎(虽不完全准确)与AI同义。深度神经网络是一类机器学习模型,将其应用到数据上的过程称为深度学习。目前,深度网络是最强大和最实用的机器学习模型之一,常见于日常生活中。我们常常用自然语言处理(Nat
- html页面js获取参数值
0624chenhong
html
1.js获取参数值js
function GetQueryString(name)
{
var reg = new RegExp("(^|&)"+ name +"=([^&]*)(&|$)");
var r = windo
- MongoDB 在多线程高并发下的问题
BigCat2013
mongodbDB高并发重复数据
最近项目用到 MongoDB , 主要是一些读取数据及改状态位的操作. 因为是结合了最近流行的 Storm进行大数据的分析处理,并将分析结果插入Vertica数据库,所以在多线程高并发的情境下, 会发现 Vertica 数据库中有部分重复的数据. 这到底是什么原因导致的呢?笔者开始也是一筹莫 展,重复去看 MongoDB 的 API , 终于有了新发现 :
com.mongodb.DB 这个类有
- c++ 用类模版实现链表(c++语言程序设计第四版示例代码)
CrazyMizzz
数据结构C++
#include<iostream>
#include<cassert>
using namespace std;
template<class T>
class Node
{
private:
Node<T> * next;
public:
T data;
- 最近情况
麦田的设计者
感慨考试生活
在五月黄梅天的岁月里,一年两次的软考又要开始了。到目前为止,我已经考了多达三次的软考,最后的结果就是通过了初级考试(程序员)。人啊,就是不满足,考了初级就希望考中级,于是,这学期我就报考了中级,明天就要考试。感觉机会不大,期待奇迹发生吧。这个学期忙于练车,写项目,反正最后是一团糟。后天还要考试科目二。这个星期真的是很艰难的一周,希望能快点度过。
- linux系统中用pkill踢出在线登录用户
被触发
linux
由于linux服务器允许多用户登录,公司很多人知道密码,工作造成一定的障碍所以需要有时踢出指定的用户
1/#who 查出当前有那些终端登录(用 w 命令更详细)
# who
root pts/0 2010-10-28 09:36 (192
- 仿QQ聊天第二版
肆无忌惮_
qq
在第一版之上的改进内容:
第一版链接:
http://479001499.iteye.com/admin/blogs/2100893
用map存起来号码对应的聊天窗口对象,解决私聊的时候所有消息发到一个窗口的问题.
增加ViewInfo类,这个是信息预览的窗口,如果是自己的信息,则可以进行编辑.
信息修改后上传至服务器再告诉所有用户,自己的窗口
- java读取配置文件
知了ing
1,java读取.properties配置文件
InputStream in;
try {
in = test.class.getClassLoader().getResourceAsStream("config/ipnetOracle.properties");//配置文件的路径
Properties p = new Properties()
- __attribute__ 你知多少?
矮蛋蛋
C++gcc
原文地址:
http://www.cnblogs.com/astwish/p/3460618.html
GNU C 的一大特色就是__attribute__ 机制。__attribute__ 可以设置函数属性(Function Attribute )、变量属性(Variable Attribute )和类型属性(Type Attribute )。
__attribute__ 书写特征是:
- jsoup使用笔记
alleni123
java爬虫JSoup
<dependency>
<groupId>org.jsoup</groupId>
<artifactId>jsoup</artifactId>
<version>1.7.3</version>
</dependency>
2014/08/28
今天遇到这种形式,
- JAVA中的集合 Collectio 和Map的简单使用及方法
百合不是茶
listmapset
List ,set ,map的使用方法和区别
java容器类类库的用途是保存对象,并将其分为两个概念:
Collection集合:一个独立的序列,这些序列都服从一条或多条规则;List必须按顺序保存元素 ,set不能重复元素;Queue按照排队规则来确定对象产生的顺序(通常与他们被插入的
- 杀LINUX的JOB进程
bijian1013
linuxunix
今天发现数据库一个JOB一直在执行,都执行了好几个小时还在执行,所以想办法给删除掉
系统环境:
ORACLE 10G
Linux操作系统
操作步骤如下:
第一步.查询出来那个job在运行,找个对应的SID字段
select * from dba_jobs_running--找到job对应的sid
&n
- Spring AOP详解
bijian1013
javaspringAOP
最近项目中遇到了以下几点需求,仔细思考之后,觉得采用AOP来解决。一方面是为了以更加灵活的方式来解决问题,另一方面是借此机会深入学习Spring AOP相关的内容。例如,以下需求不用AOP肯定也能解决,至于是否牵强附会,仁者见仁智者见智。
1.对部分函数的调用进行日志记录,用于观察特定问题在运行过程中的函数调用
- [Gson六]Gson类型适配器(TypeAdapter)
bit1129
Adapter
TypeAdapter的使用动机
Gson在序列化和反序列化时,默认情况下,是按照POJO类的字段属性名和JSON串键进行一一映射匹配,然后把JSON串的键对应的值转换成POJO相同字段对应的值,反之亦然,在这个过程中有一个JSON串Key对应的Value和对象之间如何转换(序列化/反序列化)的问题。
以Date为例,在序列化和反序列化时,Gson默认使用java.
- 【spark八十七】给定Driver Program, 如何判断哪些代码在Driver运行,哪些代码在Worker上执行
bit1129
driver
Driver Program是用户编写的提交给Spark集群执行的application,它包含两部分
作为驱动: Driver与Master、Worker协作完成application进程的启动、DAG划分、计算任务封装、计算任务分发到各个计算节点(Worker)、计算资源的分配等。
计算逻辑本身,当计算任务在Worker执行时,执行计算逻辑完成application的计算任务
- nginx 经验总结
ronin47
nginx 总结
深感nginx的强大,只学了皮毛,把学下的记录。
获取Header 信息,一般是以$http_XX(XX是小写)
获取body,通过接口,再展开,根据K取V
获取uri,以$arg_XX
&n
- 轩辕互动-1.求三个整数中第二大的数2.整型数组的平衡点
bylijinnan
数组
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class ExoWeb {
public static void main(String[] args) {
ExoWeb ew=new ExoWeb();
System.out.pri
- Netty源码学习-Java-NIO-Reactor
bylijinnan
java多线程netty
Netty里面采用了NIO-based Reactor Pattern
了解这个模式对学习Netty非常有帮助
参考以下两篇文章:
http://jeewanthad.blogspot.com/2013/02/reactor-pattern-explained-part-1.html
http://gee.cs.oswego.edu/dl/cpjslides/nio.pdf
- AOP通俗理解
cngolon
springAOP
1.我所知道的aop 初看aop,上来就是一大堆术语,而且还有个拉风的名字,面向切面编程,都说是OOP的一种有益补充等等。一下子让你不知所措,心想着:怪不得很多人都和 我说aop多难多难。当我看进去以后,我才发现:它就是一些java基础上的朴实无华的应用,包括ioc,包括许许多多这样的名词,都是万变不离其宗而 已。 2.为什么用aop&nb
- cursor variable 实例
ctrain
variable
create or replace procedure proc_test01
as
type emp_row is record(
empno emp.empno%type,
ename emp.ename%type,
job emp.job%type,
mgr emp.mgr%type,
hiberdate emp.hiredate%type,
sal emp.sal%t
- shell报bash: service: command not found解决方法
daizj
linuxshellservicejps
今天在执行一个脚本时,本来是想在脚本中启动hdfs和hive等程序,可以在执行到service hive-server start等启动服务的命令时会报错,最终解决方法记录一下:
脚本报错如下:
./olap_quick_intall.sh: line 57: service: command not found
./olap_quick_intall.sh: line 59
- 40个迹象表明你还是PHP菜鸟
dcj3sjt126com
设计模式PHP正则表达式oop
你是PHP菜鸟,如果你:1. 不会利用如phpDoc 这样的工具来恰当地注释你的代码2. 对优秀的集成开发环境如Zend Studio 或Eclipse PDT 视而不见3. 从未用过任何形式的版本控制系统,如Subclipse4. 不采用某种编码与命名标准 ,以及通用约定,不能在项目开发周期里贯彻落实5. 不使用统一开发方式6. 不转换(或)也不验证某些输入或SQL查询串(译注:参考PHP相关函
- Android逐帧动画的实现
dcj3sjt126com
android
一、代码实现:
private ImageView iv;
private AnimationDrawable ad;
@Override
protected void onCreate(Bundle savedInstanceState)
{
super.onCreate(savedInstanceState);
setContentView(R.layout
- java远程调用linux的命令或者脚本
eksliang
linuxganymed-ssh2
转载请出自出处:
http://eksliang.iteye.com/blog/2105862
Java通过SSH2协议执行远程Shell脚本(ganymed-ssh2-build210.jar)
使用步骤如下:
1.导包
官网下载:
http://www.ganymed.ethz.ch/ssh2/
ma
- adb端口被占用问题
gqdy365
adb
最近重新安装的电脑,配置了新环境,老是出现:
adb server is out of date. killing...
ADB server didn't ACK
* failed to start daemon *
百度了一下,说是端口被占用,我开个eclipse,然后打开cmd,就提示这个,很烦人。
一个比较彻底的解决办法就是修改
- ASP.NET使用FileUpload上传文件
hvt
.netC#hovertreeasp.netwebform
前台代码:
<asp:FileUpload ID="fuKeleyi" runat="server" />
<asp:Button ID="BtnUp" runat="server" onclick="BtnUp_Click" Text="上 传" />
- 代码之谜(四)- 浮点数(从惊讶到思考)
justjavac
浮点数精度代码之谜IEEE
在『代码之谜』系列的前几篇文章中,很多次出现了浮点数。 浮点数在很多编程语言中被称为简单数据类型,其实,浮点数比起那些复杂数据类型(比如字符串)来说, 一点都不简单。
单单是说明 IEEE浮点数 就可以写一本书了,我将用几篇博文来简单的说说我所理解的浮点数,算是抛砖引玉吧。 一次面试
记得多年前我招聘 Java 程序员时的一次关于浮点数、二分法、编码的面试, 多年以后,他已经称为了一名很出色的
- 数据结构随记_1
lx.asymmetric
数据结构笔记
第一章
1.数据结构包括数据的
逻辑结构、数据的物理/存储结构和数据的逻辑关系这三个方面的内容。 2.数据的存储结构可用四种基本的存储方法表示,它们分别是
顺序存储、链式存储 、索引存储 和 散列存储。 3.数据运算最常用的有五种,分别是
查找/检索、排序、插入、删除、修改。 4.算法主要有以下五个特性:
输入、输出、可行性、确定性和有穷性。 5.算法分析的
- linux的会话和进程组
网络接口
linux
会话: 一个或多个进程组。起于用户登录,终止于用户退出。此期间所有进程都属于这个会话期。会话首进程:调用setsid创建会话的进程1.规定组长进程不能调用setsid,因为调用setsid后,调用进程会成为新的进程组的组长进程.如何保证? 先调用fork,然后终止父进程,此时由于子进程的进程组ID为父进程的进程组ID,而子进程的ID是重新分配的,所以保证子进程不会是进程组长,从而子进程可以调用se
- 二维数组 元素的连续求解
1140566087
二维数组ACM
import java.util.HashMap;
public class Title {
public static void main(String[] args){
f();
}
// 二位数组的应用
//12、二维数组中,哪一行或哪一列的连续存放的0的个数最多,是几个0。注意,是“连续”。
public static void f(){
- 也谈什么时候Java比C++快
windshome
javaC++
刚打开iteye就看到这个标题“Java什么时候比C++快”,觉得很好笑。
你要比,就比同等水平的基础上的相比,笨蛋写得C代码和C++代码,去和高手写的Java代码比效率,有什么意义呢?
我是写密码算法的,深刻知道算法C和C++实现和Java实现之间的效率差,甚至也比对过C代码和汇编代码的效率差,计算机是个死的东西,再怎么优化,Java也就是和C