新的方式 E2EC: An End-to-End Contour-based Method for High-Quality High-Speed Instance Segmentation 论文笔记

写在前面

  忙的不是很彻底，继续看论文撸代码，找找灵感。
  这篇论文主要针对实例分割中的标签做了优化，列举了之前的 Polar Mask，LSNet，Deep snake 等方法的优缺点。提出自己的方法，确实很有新意。这篇文章写的也比较好，实验很是充分，是篇好文章。

• 论文地址：E2EC: An End-to-End Contour-based Method for High-Quality High-Speed Instance Segmentation
• 代码地址：https://github.com/zhang-tao-whu/e2ec
• 收录于 CVPR 2022
• 还没关注的同学点点关注，持续输出更多文章。

一、Abstract

  基于轮廓的方法使用粗糙的特征以及手工设计的轮廓初始化，限制了模型的性能；而固定式预测标签角点对的方法会导致学习困难。本文提出了一种基于轮廓的方法 E2EC。首先，应用了一种可学习的轮廓初始化方式（轮廓初始化模块+全局轮廓可变形模块）；其次，提出了一种新的标签采样计划：多方向对齐策略；再者提出了动态匹配合适的预测目标对，即动态匹配损失。数据集 KITTI INStance (KINS) ，Semantic Boundaries Dataset (SBD)，Cityscapes，COCO。在 A6000，512x512 的图片推理速度达到 36 fps。

二、引言

  上来介绍一些经典的方法，并提出不足之处。关键：通常由 128 个角点组成的轮廓能够描述大多数的实例。基于轮廓的方法仍然有很多缺点：采用手工设计的轮廓，导致不合理的路径；局部的或者有限的信息应用到轮廓的调整上，导致轮廓粗糙；局部聚合不得不无效地重复获得全局信息；GT和预测的顶点之间是固定的匹配，忽视了预测角点的轮廓位置需要调整。
  本文提出了 E2EC，主要3点贡献：可学习的轮廓初始化结构；多方向对齐；动态匹配损失函数。

• 可学习的初始化轮廓结构：轮廓初始化模块+全局轮廓可变形模块，轮廓初始化模块基于特征点中心直接回归出完整的初始化轮廓，全局轮廓可变形模块基于所有的初始轮廓点和中心点微调初始的轮廓。
  
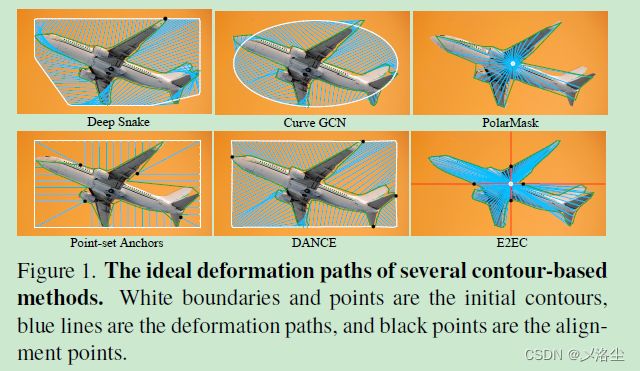
• 多方向对齐：在基于中心点的采样点上，固定住方向，因此移除了不合理的变形路径。
• 动态匹配损失 DML：去除了轮廓过于光滑的问题以及难以拟合凹凸不平点的问题。

  实验效果很厉害，如果去除了迭代的可变形模块，推理速度更快。

三、相关工作

1、基于 Mask 的实例分割方法

  遍历之前经典的双阶段/单阶段实例分割方法，指出其缺点，实时性不行，需要复杂的后处理且不能应用于模态实例分割任务上？（原文：cannot be applied to amodal instance segmentation tasks）

2、基于轮廓的实例分割方法

  缺点：通常分割质量比较粗糙。

3、其他实例分割方法

  看这一个吧，Poly Transform，训练非端到端，速度慢。

四、提出的 E2EC 方法

4.1 可学习的轮廓初始化

初始化轮廓

  首先生成热力图定位实例中心，然后根据每个初始轮廓角点的偏移量直接基于中心点回归，于是初始轮廓点就是中心点的坐标加上偏移量。

全局可变形

  $N$ 个初始点的坐标 + 1个中心点坐标通过 MLP 得到粗糙的实例轮廓（N=128）。

4.2 多方向对齐（MDA）

  通过固定一些与中心点有关的顶点方向，然后在固定点周边采样。当采样点的数量等于选取的方向时，就变成了 PolarMask，当方向选取为 0 时，就变成了 LSNet。

4.3 动态匹配损失

  损失由两部分组成：预测的角点对准标签边界上的最近邻点；关键标签点推动最近预测点朝着其本身位置移动。

  用公式表示如下：
$$\begin{array}{c}{x}_i^{\ast }=\arg {\min }_x{\Vert pre{d}_i^{in}-g{t}_x^{ipt}\Vert }_2\\ L_1(\text{ pred },gt)=\frac{1}{N}{\sum }_{i=1}^N{\Vert pre{d}_i^{\text{out }}-g{t}_{x_i^{\ast }}^{ipt}\Vert }_1\\ y_i^{\ast }=\arg {\min }_y{\Vert pre{d}_y^{in}-g{t}_i^{key}\Vert }_2\\ L_2(\text{ pred },gt)=\frac{1}{n_{key}}{\sum }_{i=1}^{n_{key}}{\Vert pre{d}_{y_i^{\ast }}^{\text{out }}-g{t}_i^{key}\Vert }_1\\ L(\text{ pred },gt)=\frac{L_1(\text{ pred },gt)+L_2(\text{ pred },gt)}{2}\end{array}$$
  其中$g{t}^{ipt}$ 表示最近的 GT 角点，$pre{d}^{in}$ 初始的轮廓点，$pre{d}^{out}$ 粗糙的轮廓点，$g{t}_i^{key}$ GT 关键点，$pre{d}_y^{in}$ 初始轮廓中的关键点，$pre{d}_{y^{\ast }}^{out}$ 粗糙轮廓中的关键点，L1 损失和 L2 损失同时使用。

4.4 实施细节

检测器

  可以基于任何检测器来实现，只需将其输出从 $H\times W\times 2$ 改为 $H\times W\times \left(N\times 2\right)$，其中 $N$ 为初始轮廓上角点的数量。这里采用 CenterNet 作为主干检测器。

损失函数

  L1 损失来监督初始化轮廓分支：
$$\begin{array}{rl}{L}_{init}& =\frac{1}{N}\sum _{i=1}^N\text{ smooth }l1\left({\tilde{x}}_i^{init}-x_i^{gt}\right)\\ L_{\text{coarse }}& =\frac{1}{N}\sum _{i=1}^N\text{ smooth }l1\left({\tilde{x}}_i^{\text{coarse }}-x_i^{gt}\right)\\ L_{i\text{ ter }1}& =\frac{1}{N}\sum _{i=1}^N\text{ smooth }l1\left({\tilde{x}}_i^{\text{iter }1},x_i^{gt}\right)\end{array}$$
  其中 ${\tilde{x}}_i^{init}$ 为预测的初始轮廓角点，${\tilde{x}}_i^{\text{coarse }}$ 为预测的粗糙轮廓角点，$x_i^{gt}$ 为标签轮廓角点，${\tilde{x}}_i^{\text{iter }1}$ 为变形后的轮廓角点。

  接下来是 DML 损失函数：
$$\begin{array}{c}{L}_{i\text{ ter }2}=L_{DML}\left({\tilde{x}}_i^{i\text{ ter }2},x_i^{gt}\right)\\ L_{i\text{ ter }}=L_{i\text{ ter }1}+L_{i\text{ ter }2}\end{array}$$其中 ${\tilde{x}}_i^{i\text{ ter }2}$ 为第二个可变形模块中变形后的轮廓角点。

  整体损失为：
$$L_{\text{overall }}=L_{\text{det }}+\alpha L_{init}+\beta L_{\text{coarse }}+\beta$$其中 $\alpha =\beta =0.1$，$L_{\text{det }}$ 为中心点的检测损失。

五、数据集

5.1 数据集和指标

数据集

  采用 KINS，SBD，Cityscapes，COCO 数据集。

指标

  标准的 $\text{AP}$ 以及 ${\text{AP}}^{msk}$ 表示分割质量，${\text{AP}}^{bdy}$ 表示边框质量。

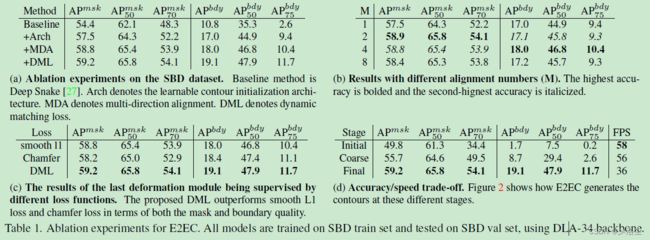
5.2 消融实验

  150 个 epochs，多尺度数据增强，学习率 $0.0001$ 在 80 和 120 epochs 时衰减一半。

可学习的角点初始化架构

  如表 1 (a) 所示。

多方向对齐

  如表 1 (b) 所示。可视化结果：

动态匹配损失

  如表 1（c） 所示。可视化结果：

速度 vs. 精度

  如表 1(d) 所示。可视化结果图 7。

5.3 与最先进方法的性能比较

在 KINS 数据集上

  测试在单个分辨率为 768x2496 的图像上，结果如下表所示，

可视化结果：

在 SBD 数据集上

  使用多尺度训练，输入单张分辨率图像为 512x512，结果如下表所示：


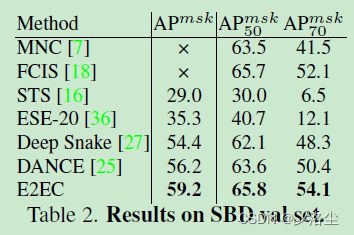
可视化的结果如图 9 所示。

在 Cityscapes 数据集上

  多尺度训练，测试在单张分辨率为 1216×2432 的图像上进行。
  表 5 和表 4，可视化结果图 9。

在 COCO 数据集上

六、结论

  本文提出了由3个模块组成的 E2EC，在数据集上性能很好，去除可变形模块后，FPS 很高。

写在后面
  这篇文章写作和创新点都很好，既对前面的方法进行了总结，又将自己的方法做足了实验，值得精度。
  还没关注的同学点点关注，持续输出干货文章。