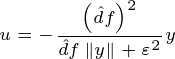机器人动力学与控制学习笔记(六)————机器人PID控制
六、机器人鲁棒自适应PD控制
6.1 问题的提出
对于具有强耦合性和非线性的机器人系统而言,线性PD控制是最为简单且行之有效的控制方法,在工业机器人中得到了广泛应用。但实践表明,线性PD控制往往要求驱动机构有很大的初始输出,而实际驱动机构(通常是电机)往往不可能提供过大的初始力矩,且机械臂本身所承受的最大力矩也是有限的,这将使通过增大PD控制系数来进一步提高系数的性能受到限制。鉴于此,很多非线性PD控制方法被提出了出来,但常规的非线性PD控制器只有单纯的PD项,要求比例和微分项的系数仍较大,存在输出力矩较大的问题。
现有一种自适应鲁棒PD控制策略,避免了初始输出力矩过大的弊端。该控制器由非线性PD反馈和补偿控制两部分构成,机器人不确定动力学部分由回归矩阵构成的自适应控制器进行补偿,并针对机器人 有界扰动的上确界是否已知设计了两种不同的扰动补偿法。该控制策略的优点在于当初始误差较大时,PD反馈起主要作用,通过非线性PD控制,避免了过大初始力矩输出;当误差较小时,自适应控制器起着主要的作用,从而保证了系统具有良好的动态性能。
6.2 机器人动力学模型及其结构特性
考虑一个N关节的机器人力臂,其动态性能可以由以下二阶非线性微分方程描述:
![]()
![]() (6.7)
(6.7)
式中:![]() 为关节角位移量,
为关节角位移量,![]() 为机器人的惯性矩阵,
为机器人的惯性矩阵,![]() 表示离心力和哥氏力,
表示离心力和哥氏力,![]() 为重力项,
为重力项,![]() 为控制力矩,
为控制力矩,![]() 为各种误差和扰动。
为各种误差和扰动。
机器人系统的动力学特性如下:
- 特性1
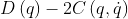 是一个斜对称矩阵。
是一个斜对称矩阵。 - 特性2 惯性矩阵
 是对称正定矩阵,存在正数
是对称正定矩阵,存在正数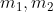 满足如下不等式:
满足如下不等式:
![]() (6.8)
(6.8)
- 特性3 存在一个依赖于机械手参数的参数向量,使得
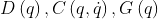 满足线性关系:
满足线性关系:
![]() (6.9)
(6.9)
其中,![]() 为已知关节变量函数的回归矩阵,它是机器人广义坐标及其各阶导数的已知函数矩阵;
为已知关节变量函数的回归矩阵,它是机器人广义坐标及其各阶导数的已知函数矩阵;![]() 是描述机器人质量特性的未知定常参数向量。
是描述机器人质量特性的未知定常参数向量。
假设1 ![]() 为期望的关节角位移,
为期望的关节角位移,![]() 的一阶导数和二阶导数存在。
的一阶导数和二阶导数存在。
假设2 误差和扰动![]() 的范数满足:
的范数满足:
![]() (6.10)
(6.10)
其中,![]() 分别为正常数,
分别为正常数,![]() 分别为跟踪误差和跟踪误差导数。
分别为跟踪误差和跟踪误差导数。
6.3 控制器的设计
分别引入变量![]() 和
和![]() ,并令:
,并令:
![]() (6.11)
(6.11)
![]() (6.12)
(6.12)
其中常数![]() ,则可推出:
,则可推出:
![]() (6.13)
(6.13)
由式(6.9)中的机器人线性关系特性,取![]() ,得:
,得:
![]() (6.14)
(6.14)
由式(6.13)得![]() ,将其代入上式,得:
,将其代入上式,得:
![]()
将上式结合式(6.7),得:
![]() (6.15)
(6.15)
1.扰动信号的上确界已知时控制器的设计
对于式(6.7)所示的机器人系统,在误差扰动信号的上确界已知时,采用以下控制器和自适应律,可保证系统全局渐进稳定。
![]() (6.16)
(6.16)
![]() ,
,![]() (6.17)
(6.17)
![]() 的参数估计律取:
的参数估计律取:
![]() (6.18)
(6.18)
式中
![]()
![]()
![]()
其中![]() 均大于零,
均大于零,![]() 为正定对称阵。
为正定对称阵。
证明过程略。
2.扰动信号的上确界未知时控制器的设计
定理 当误差扰动信号![]() 的上确界为未知时,设计控制器为:
的上确界为未知时,设计控制器为:
![]() (6.21)
(6.21)
![]() (6.23)
(6.23)
![]() (6.24)
(6.24)
其中![]() 的取值同式(6.16),并保证满足式(6.19),
的取值同式(6.16),并保证满足式(6.19),![]() 的估计值
的估计值![]() 通过式(6.18)求得,
通过式(6.18)求得,![]() ,
,![]() ,,
,,![]() 为
为![]() 的估值,
的估值,![]() 均为任意的正常数。
均为任意的正常数。
对式(6.7)所示的机器人系统,并且误差扰动信号的上确界未知时,采用式(6.21)和式(6.22)的控制律可保证系统全局渐进稳定。
证明过程略。
6.4 机器人动态方程的线性化推导
考虑动态方程:
![]()
为了实现控制律式(6.16)、式(6.17)和自适应律式(6.18),必须给出式(6.28)中![]() 和
和![]() 的表达。
的表达。
针对双力臂机器人动态方程:
(6.26)
其中
![]()
![]()
![]()
![]()
![]()
![]()
则式(6.25)中的第一个关节方程为:
则式(6.25)中的第二个关节方程为:
根据机器人系统的动力学特性3,取回归矩阵![]() 的表达式为:
的表达式为:
![]()
![]()
![]()
![]()
![]()
可见,由于![]() 的表达式不含有
的表达式不含有![]() 和
和![]() ,故本控制算法可实现变负载的机械手控制。
,故本控制算法可实现变负载的机械手控制。
6.5 仿真实例
被控对象为双力臂机器人动态方程式(6.26),![]() 。
。
误差扰动、位置指令和系统的初始状态分别为:
![]()
控制参数取
![]()
![]()
采用S函数进行控制器和被控对象的设计。按扰动上确界已知和未知两种情况进行仿真。
仿真之一
仿真程序
控制主程序:chap2_2sim.mdl
指令信号子程序:chap2_2input.m
function[sys,x0,str,ts] = chap2_2input(t,x,u,flag)
switch flag
case 0
[sys,x0,str,ts] = mdlInitializeSizes;
case 3
sys = mdlOutputs(t,x,u);
case {2,4,9}
sys = [];
otherwise
error(['Unhandled flag = ',num2str(falg)]);
end
function[sys,x0,str,ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumOutputs = 6;
sizes.NumInputs = 0;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 =[];
str =[];
ts =[];
function sys = mdlOutputs(t,x,u)
q1_d = sin(2*pi*t); %关节1期望的角位移
q2_d = sin(2*pi*t); %关节2期望的角位移
dq1_d = 2*pi*cos(2*pi*t); %关节1期望的角位移的导数
dq2_d = 2*pi*cos(2*pi*t); %关节1期望的角位移的导数
ddq1_d = -(2*pi)^2*sin(2*pi*t); %关节1期望的角位移的二阶导数
ddq2_d = -(2*pi)^2*sin(2*pi*t); %关节1期望的角位移的二阶导数
sys(1) = q1_d; %赋值给sys,一共6个输入
sys(2) = dq1_d;
sys(3) = ddq1_d;
sys(4) = q2_d;
sys(5) = dq2_d;
sys(6) = ddq2_d;
控制器子程序:chap2_2ctrl.m
%本文件是控制策略
function [sys,x0,str,ts] = chap2_2ctrl(t,x,u,flag)
switch flag
case 0
[sys, x0,str,ts] = mdlInitializeSizes;
case 3
sys = mdlOutputs(t,x,u);
case{2,4,9}
sys = [];
otherwise
error(['Unhandled flag =',num2str(flag)]);
end
function [sys,x0,str,ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumOutputs = 2;
sizes.NumInputs = 13;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 = [];
str =[];
ts = [];
function sys = mdlOutputs(t,x,u)
q1_d = u(1);dq1_d = u(2);ddq1_d = u(3); %关节1期望的角位移,导数,二阶导数
q2_d = u(4);dq2_d = u(5);ddq2_d = u(6); %关节2期望的角位移,导数,二阶导数
q1 = u(7);dq1 = u(8); %关节1实际的角位移及导数
q2 = u(9);dq2 = u(10); %关节2实际的角位移及导数
dq_d = [dq1_d,dq2_d]' ; %关节1和关节2期望的角位移的导数矩阵
ddq_d = [ddq1_d,ddq2_d].'; %矩阵加单引号表示共轭转置,不仅交换行列,还改变虚部符号
e = [q1-q1_d,q2-q2_d].'; %跟踪误差
de = [dq1-dq1_d,dq2-dq2_d].'; %跟踪误差导数
gama = 5*eye(2); %eye(2)表示生成2*2单位矩阵
y = gama.*e+de; %变量y
dqr = dq_d-gama.*e; %变量dqr是二维列向量
ddqr = ddq_d-gama.*de;
%扰动信号的上确界已知时控制器的设计
d1 = 2;d2 = 3;d3 = 6;
u1 = -(d1+d2*norm([e(1),e(2)])+d3*norm([de(1),de(2)]))*sign(y(1)); %norm([e(1),e(2)])是范数,求e(1)的平方加e(2)的平方和再开根号
u2 = -(d1+d2*norm([e(1),e(2)])+d3*norm([de(1),de(2)]))*sign(y(2));
Kp1 = [180,0;0,190];
Kp2 = [150,0;0,150];
Kv1 = [180,0;0,190];
Kv2 = [150,0;0,150];
alfa1 = 1;alfa2 = 1;
beta1 = 1;beta2 = 1;
p1 = u(11);
p2 = u(12);
p3 = u(13);
P = [p1 p2 p3].';
r1 = 1;g = 9.8;e1 = g/r1;
fai11 = ddqr(1)+e1*cos(q2);
fai12 = ddqr(1)+ ddqr(2);
fai13 = 2*ddqr(1)*cos(q2)+ddqr(2)*cos(q2)-dq2*dqr(1)*dqr(1)*sin(q2)-(dq1+dq2)*dqr(2)*sin(q2)+e1*cos(q1+q2);
fai21 = 0;
fai22 = fai12;
fai23 = dq1*dqr(1)*sin(q2)+ddqr(1)*cos(q2)+e1*cos(q1+q2);
FAI = [fai11 fai12 fai13;fai21 fai22 fai23];
R = FAI * P;
tol(1) = -(Kp1(1,1)+Kp2(1,1)/(alfa1+abs(e(1))))*e(1)-(Kv1(1,1)+Kv2(1,1)/(beta1+abs(de(1))))*de(1)+R(1)+u1; %控制力矩tol
tol(2) = -(Kp1(2,2)+Kp2(2,2)/(alfa2+abs(e(2))))*e(2)-(Kv1(2,2)+Kv2(2,2)/(beta2+abs(de(2))))*de(2)+R(2)+u2; %控制力矩tol
sys(1) = tol(1);
sys(2) = tol(2);
自适应算法子程序:chap2_2adapt.m
%机器人自适应控制律
function [sys,x0,str,ts] = chap2_2adapt(t,x,u,flag)
switch flag
case 0
[sys, x0,str,ts] = mdlInitializeSizes;
case 1
sys = mdlDerivatives(t,x,u);
case 3
sys = mdlOutputs(t,x,u);
case{2,4,9}
sys = [];
otherwise
error(['Unhandled flag =',num2str(flag)]);
end
function [sys,x0,str,ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 3;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 3;
sizes.NumInputs = 10;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 = [4.1,1.9,1.7];
str =[];
ts = [];
function sys = mdlDerivatives(t,x,u)
q1_d = u(1);dq1_d = u(2);ddq1_d = u(3);
q2_d = u(4);dq2_d = u(5);ddq2_d = u(6);
q1 = u(7);dq1 = u(8);
q2 = u(9);dq2 = u(10);
q_error = [q1-q1_d,q2-q2_d]';
dq_error = [dq1-dq1_d,dq2-dq2_d]';
gama = 5*eye(2);
y = gama*q_error+dq_error;
ddq_d = [ddq1_d,ddq2_d]';
dq_d = [dq1_d,dq2_d]';
dqr = dq_d-gama*q_error;
ddqr = ddq_d-gama*dq_error;
g = 9.8; r1 =1;
e1 = g/r1;
fai11 = ddqr(1)+e1*cos(q2);
fai12 = ddqr(1)+ddqr(2);
fai13 = 2*ddqr(1)*cos(q2)+ddqr(2)*cos(q2)-dq2*dqr(1)*sin(q2)-(dq1+dq2)*dqr(2)*sin(q2)+e1*cos(q1+q2);
fai21 = 0;
fai22 = fai12;
fai23 = dq1*dqr(1)*sin(q2)+ddqr(1)*cos(q2)+e1*cos(q1+q2);
FAI =[fai11 fai12 fai13;fai21 fai22 fai23];
Gama = 5*eye(3);
S = -Gama*FAI'*y;
for i=1:1:3
sys(i)=S(i);
end
function sys = mdlOutputs(t,x,u)
sys(1) = x(1);
sys(2) = x(2);
sys(3) = x(3);
被控对象子程序:chap2_2plant.m
%机器人平台
function [sys,x0,str,ts] = chap2_2plant(t,x,u,flag)
switch flag
case 0
[sys, x0,str,ts] = mdlInitializeSizes;
case 1
sys = mdlDerivatives(t,x,u);
case 3
sys = mdlOutputs(t,x,u);
case{2,4,9}
sys = [];
otherwise
error(['Unhandled flag =',num2str(flag)]);
end
function [sys,x0,str,ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 4;
sizes.NumDiscStates = 0;
sizes.NumOutputs = 4;
sizes.NumInputs = 2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0 = [0.10,0,0.10,0];
str =[];
ts = [];
function sys = mdlDerivatives(t,x,u)
q1_d = sin(2*pi*t); %给定关节1的期望轨迹
q2_d = sin(2*pi*t); %给定关节2的期望轨迹
dq1_d = 2*pi*cos(2*pi*t); %给定关节1的期望轨迹的导数
dq2_d = 2*pi*cos(2*pi*t); %给定关节2的期望轨迹的导数
%ddq1_d = -(2*pi)^2*sin(2*pi*t); %给定关节1的期望轨迹的二阶导数
%ddq2_d = -(2*pi)^2*sin(2*pi*t); %给定关节2的期望轨迹的二阶导数
e(1) = x(1)-q1_d; %关节1角位移的跟踪误差
e(2) = x(3)-q2_d; %关节2角位移的跟踪误差
de(1) = x(2)-dq1_d; %关节1角位移的跟踪误差的导数
de(2) = x(4)-dq2_d; %关节2角位移的跟踪误差的导数
tol = [u(1);u(2)];
q1 = x(1);
dq1 = x(2);
q2 = x(3);
dq2 = x(4);
m1 = 0.5;m2 = 0.5; %机器人的双臂连杆的质量
r1 = 1;r2 = 0.8; %机器人的双臂连杆端点到质心之间的距离
g = 9.8; %重力加速度g
D11 = (m1+m2)*r1^2+m2*r2^2+2*m2*r1*r2*cos(q2); %机器人的惯性矩阵
D12 = m2*r2^2+m2*r1*r2*cos(q2); %机器人的惯性矩阵
D22 = m2*r2^2; %机器人的惯性矩阵
D = [D11 D12;D12 D22]; %机器人的惯性矩阵
C12 = m2*r1*r2*sin(q2); %机器人的离心力和哥氏力
C = [-C12*dq2 -C12*(dq1+dq2);C12*dq1 0]; %机器人的离心力和哥氏力
g1 = (m1+m2)*r1*cos(q2)+m2*r2*cos(q1+q2); %机器人的重力项
g2 = m2*r2*cos(q1+q2); %机器人的重力项
G = [g1*g;g2*g]; %机器人的重力项
w = [1.5;1.5]+2.0*[e(1);e(2)]+5.0*[de(1);de(2)]; %其余误差和扰动
S = inv(D).*(tol-[dq1;dq2].*C-G-w); %S为给定关节的期望轨迹的二阶导数,即ddq
sys(1)=x(2); %给定关节1的实际轨迹的导数
sys(2)=S(1); %
sys(3)=x(4); %给定关节2的实际轨迹的导数
sys(4)=S(2); %
function sys = mdlOutputs(t,x,u)
sys(1) = x(1); %给定关节1的实际轨迹
sys(2) = x(2); %给定关节1的实际轨迹的导数
sys(3) = x(3); %给定关节1的实际轨迹
sys(4) = x(4); %给定关节1的实际轨迹的导数
作图子程序:chap2_2plot.m
close all;
t = out.t.Data;
qd = out.qd.Data;
q = out.q.Data;
p = out.p.Data;
figure(1);
subplot(211);
plot(t,qd(:,1),'r',t,q(:,1),'b');
xlabel('time(s)');
ylabel('position tracking of link 1');
subplot(212);
plot(t,qd(:,2),'r',t,q(:,2),'b');
xlabel('time(s)');
ylabel('velocity tracking of link 1');
figure(2);
subplot(211);
plot(t,qd(:,4),'r',t,q(:,3),'b');;
xlabel('time(s)');
ylabel('position tracking of link 2');
subplot(212);
plot(t,qd(:,5),'r',t,q(:,4),'b');
xlabel('time(s)');
ylabel('velocity tracking of link 2');
m1 = 0.5;m2 = 0.5;
r1 = 1; r2 = 0.8;
p1 = (m1+m2)*r1^2;
p2 = m2*r2^2;
p3 = m2*r1*r2;
figure(3);
subplot(311);
plot(t,p(:,1),'r',t,p1,'b');
xlabel('time(s)');
ylabel('p1 estimate value');
subplot(312);
plot(t,p(:,2),'r',t,p2,'b');
xlabel('time(s)');
ylabel('p2 estimate value');
subplot(313);
plot(t,p(:,3),'r',t,p3,'b');
xlabel('time(s)');
ylabel('p3 estimate value');