阅读笔记:《机器学习》西瓜书(9)——聚类
聚类
- 聚类任务
- 性能度量
-
- 外部指标
- 内部指标
- 距离计算
-
- 有序属性的距离计算
- 无序属性的距离计算
- 原型聚类
-
- k均值算法
- 学习向量量化
- 高斯混合聚类
- 密度聚类
-
- DBSCAN
- 层次聚类
-
- AGNES
聚类任务
在无监督学习中,由于训练样本并没有标签,一般使用聚类来揭示训练样本数据中的内在规律,为进一步的数据分析提供基础。聚类试图将训练样本在属性空间(特征空间、样本空间)中划分出若干个通常不相交的子集(簇)。这样,每个簇就对应于一些潜在的类别。
为了保证聚类过程的正确性,需要使用一种定量的指标进行描述,这种指标称为性能度量,用于评估聚类结果的好坏。在聚类过程中,为了将潜在的同类样本分在一类,一般会采用一种方法来描述不同样本间的距离,这种方法称作距离计算,显然需要使潜在的同类样本其距离越紧越好。
性能度量
通过构造某种性能度量,我们可以描述聚类结果的好坏。一般来说,我们希望聚类结果的簇内相似度高且簇间相似度低。
聚类的性能度量一般分为两种,一种是外部指标,即将聚类结果与某一个参考模型进行比较;另一种是内部指标,即不使用任何参考模型,直接考察聚类结果。
外部指标
对于数据集 D = x 1 , x 2 , … , x m D={\boldsymbol{x_1},\boldsymbol{x_2},\dots,\boldsymbol{x_m}} D=x1,x2,…,xm,若通过聚类给出簇划分KaTeX parse error: Undefined control sequence: \C at position 28: …{C_1,C_2,\dots,\̲C̲_k},参考模型给出的簇划分为 C ∗ = C 1 ∗ , C 2 ∗ , … , C s ∗ \mathcal{C}^*={C_1^*,C_2^*,\dots,C_s^*} C∗=C1∗,C2∗,…,Cs∗,令 λ \lambda λ和 λ ∗ \lambda^* λ∗分别表示待评价聚类和参考模型对应的簇标记。定义:

这里,有 a + b + c + d = m ( m − 1 ) 2 a+b+c+d=\frac{m(m-1)}{2} a+b+c+d=2m(m−1)成立。
常用的聚类性能度量的外部指标如下:


上述性能度量的结果在 [ 0 , 1 ] [0,1] [0,1]之间,且值越大越好。
内部指标

其中, dist ( ⋅ , ⋅ ) \text{dist}(\cdot,\cdot) dist(⋅,⋅)用于计算两个样本间的距离, μ \boldsymbol{\mu} μ表示簇 C C C的中心点 μ = 1 C ∑ 1 ≤ i ≤ ∣ C ∣ \boldsymbol{\mu}=\frac{1}{C}\sum_{1\leq i\leq |C|} μ=C1∑1≤i≤∣C∣, avg ( C ) \text{avg}(C) avg(C)表示簇 C C C内个样本间的平均距离, diam ( C ) \text{diam}(C) diam(C)表示簇 C C C内样本的最大距离, d min ( C i , C j ) d_{\min}(C_i,C_j) dmin(Ci,Cj)表示两簇样本彼此的最近距离, d den ( C i , C j ) d_{\text{den}}(C_i,C_j) dden(Ci,Cj)表示两簇样本中心点的距离。
常用的聚类性能度量的内部指标如下:

显然, DBI 的值越小越好,而DI 则相反,值越大越好。
距离计算
函数 dist ( ⋅ , ⋅ ) \text{dist}(\cdot,\cdot) dist(⋅,⋅)用于计算两个样本间的距离。一般来说,我们习惯于将样本的各属性表示在一个向量中,然后通过某种距离的定义计算两个向量间的距离。然而在实际应用过程中,并不是所有的属性值都能直接定量进行表示。我们一般称能够定量表示的属性为有序属性,反之为无序属性。
有序属性的距离计算
对给定的样本 x i = ( x i 1 ; x i 2 ; … ; x i n ) \boldsymbol{x_i}=(x_{i1};x_{i2};\dots;x_{in}) xi=(xi1;xi2;…;xin)与 x j = ( x j 1 ; x j 2 ; … ; x j n ) \boldsymbol{x_j}=(x_{j1};x_{j2};\dots;x_{jn}) xj=(xj1;xj2;…;xjn),最常用的距离计算方法为闵可夫斯基距离(Minkowski distance):
dis m k ( x i , x j ) = ( ∑ u = 1 n ∣ x i u − x j u ∣ p ) 1 p \text{dis}_{mk}(\boldsymbol{x_i},\boldsymbol{x_j})={\Bigg( \sum_{u=1}^n{{|x_{iu}-x_{ju}|}^p}\Bigg)}^{\frac{1}{p}} dismk(xi,xj)=(u=1∑n∣xiu−xju∣p)p1
无序属性的距离计算
对于无序属性,一般采用VDM方法来量化各属性值间的距离,然后结合闵可夫斯基距离即可计算不同样本间的距离。
假设有 n c n_c nc个有序属性, n − n c n-n_c n−nc个无序属性,有:

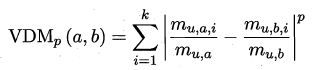
其中 m u , a m_{u,a} mu,a表示在属性 u u u上取值为 a a a的样本数, m u , a , i m_{u,a,i} mu,a,i表示在簇 C i C_i Ci中在属性 u u u上取值为 a a a的样本数。
此外,当样本空间中不同属性的重要性不同时,可使用"加权距离。
原型聚类
此类算法假设聚类结构能通过一组原型刻画。算法先对原型进行初始化,然后对原型进行迭代更新求解。
k均值算法
k均值算法先随机选取k(待分类类别数)个样本点作为初始均值向量,然后通过更新离均值向量更近的点为均值向量对应的类别,再重新计算各类别均值向量的方式,不断迭代直到均值向量无法再被更新。算法流程如下:

学习向量量化
学习向量量化也先初始化一组原型向量,然后随机选取样本点并找到离样本点最近的原型向量,根据原型向量与该样本点是否同类别来更新原型向量:相同类别则原型向量按一定步长靠近样本点,反之则远离。算法流程如下:

高斯混合聚类
这种方法采用概率模型而非原型向量来描述聚类原型。它假设对于每个类别来说,样本 x \boldsymbol{x} x服从高斯分布:
p ( x ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 e − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) p(\boldsymbol{x})=\frac{1}{{(2\pi)}^{\frac{n}{2}}{|\Sigma|}^{\frac{1}{2}}}e^{-\frac{1}{2}{(\boldsymbol{x}-\boldsymbol{\mu})^\boldsymbol{T}\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})}} p(x)=(2π)2n∣Σ∣211e−21(x−μ)TΣ−1(x−μ)
因此,对于 k k k个类别来说,对样本 x \boldsymbol{x} x,有高斯混合分布:
p M ( x ) = ∑ i = 1 k α i ⋅ p ( x ∣ μ i , Σ i ) p_{\mathcal{M}}(\boldsymbol{x})=\sum_{i=1}^{k}{\alpha_i \cdot p(\boldsymbol{x}\mid \boldsymbol{\mu_i},\Sigma_i)} pM(x)=i=1∑kαi⋅p(x∣μi,Σi)
α i \alpha_i αi为混合系数,令 ∑ i = 1 k α i = 1 \sum_{i=1}^k{\alpha_i}=1 ∑i=1kαi=1。
这样,只要能够确定样本 x j \boldsymbol{x_j} xj是由哪个高斯分布生成的(这里用 z j z_j zj表示),即可确定该样本属于哪一类。这种选择可由样本确定的条件下计算各类的后验概率得到。根据贝叶斯定理:

这个后验给出了样本 x j \boldsymbol{x_j} xj是由第 i i i个高斯混合成分生成的概率,也即其属于第 i i i类的概率,将其简记为 γ j i \gamma_{ji} γji。因此,对于每个样本 x j \boldsymbol{x_j} xj的簇标记 λ j \lambda_j λj,应有:
λ j = arg max i ∈ 1 , 2 , … , k γ j i \lambda_j=\mathop{\arg\max}\limits_{i\in{1,2,\dots,k}}{\gamma_{ji}} λj=i∈1,2,…,kargmaxγji
从原型聚类的角度来看,高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画,簇划分则由原型对应的后验概率确定。
为求解模型参数 ( α i , μ i , Σ i ) ∣ 1 ≤ i ≤ k {(\alpha_i,\boldsymbol{\mu_i},\boldsymbol{\Sigma_i})\mid 1\leq i\leq k} (αi,μi,Σi)∣1≤i≤k:

一般使用EM算法进行迭代求解。
高斯混合聚类算法流程如下:

其中提到的式9.30即是上述提到的样本确定的条件下其属于某一类的后验概率。
密度聚类
此类算法假设聚类结构能通过样本分布的紧密程度确定。一般通过考察样本间的可连接性,不断扩展聚类簇以得到最终结果。
DBSCAN
DBSCAN是一种著名的密度聚类算法。这种算法通过 ϵ \epsilon ϵ-邻域和邻域中的样本个数 M i n P t s MinPts MinPts来构建可连接性,并根据是否可连接进行分类。其算法流程如下:

层次聚类
层次聚类试图在不同层次对数据集进行划分(自底向上或自顶向下),从而形成树形的聚类结构。
AGNES
AGNES是一种采用自底向上聚合策略的层次聚类法。它先将数据集中的每个样本看作一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复,直至达到预设的聚类簇个数。根据聚类簇间距离计算方式的不同,AGNES 算法被相应地称为“单链接”(最小距离)、“全链接”(最大距离)或“均链接”(平均距离)算法。