阅读笔记：STANet

STANet

1.解决的问题

给定两幅在不同时间拍摄的共配准图像，光照变化和配准误差淹没了真实物体的变化。

在不同时间拍摄的两幅共配准图像中，光照变化和光照角度变化引起的配准误差压倒了真实物体的变化，对CD算法提出了挑战。从图1a中我们可以看到，两幅图像的对比度和亮度，以及建筑的空间纹理是不同的。在双时相图像中，由于太阳位置的变化，会产生不同的建筑阴影。从图1b可以看出，在两幅共配准图像中，对应建筑物的边缘出现了明显的误配误差。如果不小心处理，它们可能会在未改变的建筑的边界上造成错误的检测。

2.提出的策略

本文提出了一种新的基于孪生网络的时空注意神经网络。与以往方法不同的是，我们利用时空依赖性。

• 我们设计了一种CD自注意力机制来对时空关系进行建模，在特征提取过程中增加了一个CD自注意力模块。我们的自我注意模块计算任意两个像素在不同时间和位置之间的注意权重，并使用它们来生成更具区别性的特征。
• 由于目标可能会有不同的尺度，我们将图像分割成多尺度的子区域，并在每个子区域引入自注意，这样就可以在不同尺度捕获时空依赖性，从而生成更好的表示，以适应各种大小的对象。

本文的另一个贡献就是提出一个新的变化检测数据集LEVIR-CD，比该领域的其他公共数据集大两个数量级。

图片来源：双时态谷歌地球图片；

数据集大小：637对1024x1024的图片，超过31k个独立标记的变更实例。

在可接受的计算开销下，我们提出的注意力模块将基线模型的f1得分从83.9提高到87.3。在一个公共遥感图像CD数据集上的实验结果表明，我们的方法优于其他几种先进的方法。

3.框架解读

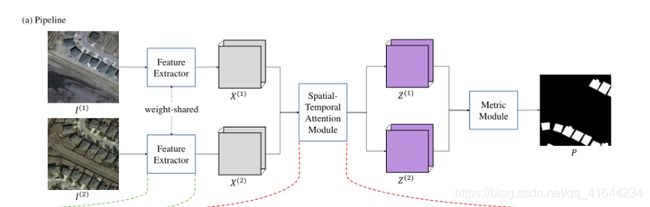
两个$H_0\ast W_0$d的双时间遥感图像，$I^{(1)}$，$I^{(2)}$，CD生成一个label Map $M$，尺寸和输入图片相同，其中每一个空间位置都需要分配变化的类别(改变为1，不变为0)。

网络由三部分组成;

• 特征提取器
• 注意力模块
• 度量模块

1.首先，将两幅图像依次输入特征提取器(一个FCN，例如没有完全连接层的ResNet )，得到两个特征映射$X^{(1)}$，$X^{(2)}$∈$R^{C\times H\times W}$，$H\ast W$为特征映射大小，$C$为每个特征向量通道个数。

2.注意模块将这些特征映射更新为两个注意特征映射$Z^{(1)}$和$Z^{(2)}$。

3.调整更新特性映射到输入图像的大小之后,度量模块计算两个特征图中每个像素对之间的距离，生成distance map D。

4.在训练阶段,我们的模型优化通过计算的distance map和label map的最小化损失,使变化点的距离值大，不变点的距离值小。

5.而在测试阶段，可以通过简单的distance map 阈值计算预测 label map P。

3.1 特征提取器

我们设计了一个类似fcn的特征提取器，基于ResNet-18。

？为什么使用ResNet-18

因为最初的ResNet是为图像分类任务而设计的，它包含一个全局池化层和一个完全连接的层，用于将图像特征映射到1000维向量(ImageNet中类别的数量)。而我们的CD任务是一个密集分类任务，需要获得与输入图像相同大小的change。

因此，我们省略了原ResNet的全局池化层和全连接层。其余部分分为五个阶段;每个人的步幅是2。

CNN的高级特征在语义上是准确的，但在位置上是粗糙的，而低级特征包含精细的细节，但缺乏语义信息。因此，我们融合了高级语义信息和低级空间信息来生成更精细的表示。

我们将最后一个阶段的输出特征映射输入卷积层(C1, 1 × 1/1)，将其维数变换为C1。请注意，卷积层的配置是“滤波器的数量，大小/步幅”，为了简单起见，省略了批标准化(BN)和ReLU层。同样，将第2、3、4阶段的输出特征图分别输入到3个不同的卷积层;每个通道维度都转换为C1。然后，我们将最后三个阶段转换后的特征映射调整为输入图像的1/4大小。

我们从网络的不同阶段得到了4组特征映射。这4个特征图在通道维数上连接(得到4× C1)，并送入两个不同的卷积层(C2, 3× 3/1;C3, 1× 1/1)生成最终特征图。这两个卷积层通过利用局部空间信息和降低特征通道维数可以生成更有区别性和紧凑的表示。在实现中，我们将C1设置为96，C2设置为256，C3设置为64，以在效率和准确性之间进行权衡。

mynet3(
  (backbone): ResNet(
    (conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
    (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (relu): ReLU(inplace=True)
    (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
    (layer1): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicBlock(
        (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (layer2): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (layer3): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (layer4): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(2, 2), dilation=(2, 2), bias=False)
        (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
      (2): BasicBlock(
        (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(4, 4), dilation=(4, 4), bias=False)
        (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
  )
  (decoder): Decoder(
    (dr2): DR(
      (conv1): Conv2d(64, 96, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(96, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU()
    )
    (dr3): DR(
      (conv1): Conv2d(128, 96, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(96, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU()
    )
    (dr4): DR(
      (conv1): Conv2d(256, 96, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(96, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU()
    )
    (dr5): DR(
      (conv1): Conv2d(512, 96, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(96, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU()
    )
    (last_conv): Sequential(
      (0): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (2): ReLU()
      (3): Dropout(p=0.5, inplace=False)
      (4): Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (5): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (6): ReLU()
    )
  )
)

3.2 时空关注模块

自注意机制在模拟长期时空依赖性中是有效的。在此认知的驱动下，我们设计了一种CD自注意机制，该机制能够捕获整个时空中个体像素之间丰富的全局时空关系，从而获得更多的识别特征。

我们设计了两种自注意力模块：一个基础的时空注意力模块（BAM），一个金字塔时空注意力模块（PAM）。

BAM学习捕捉任意两个位置之间的时空相关性(注意力权重)，并通过时空中所有位置特征的加权和计算每个位置的响应。

PAM将BAM嵌入到金字塔结构中，去生成多尺度注意力表示。

BAM

输入：$X^{(1)}$，$X^{(2)}$叠加后的特征向量，$X\in R^{C\times H\times W\times 2}$

输出：更新后的特征向量Z,$Z\in R^{C\times H\times W\times 2}$

利用残差网络从X得到Z：$Z=F(X)+X$，$Y=F(X)$是待学习X的残差映射。

?如何生成$Y$

计算Y的核心是从输入张量中生成一组键向量(keys)、值向量(values)和查询向量(queries)，并学习这些值的加权总和来生成每个输出向量，其中分配给每个值的权重取决于查询和对应键的相似度。

• $X$首先转化为两个特征张量$Q，K\in R^{C’\times H\times W\times 2}$。Q和K分别由两个不同的卷积层($C^{\prime }$, 1× 1/1)得到。我们将它们重塑为关键矩阵$K^{-}$和查询矩阵$Q^{-}$，其中N = H × W × 2为输入特征向量的个数。关键矩阵和查询矩阵用于以后计算注意力。

• 我们把X输入另一个卷积层(C, 1× 1/1)，生成一个新的特征张量$V\in R^{C\times H\times W\times 2}$。我们把它重新塑造成一个值矩阵$V^{-}$。$C^{\prime }$是键和查询的特征维度。在我们的实现中，$C^{\prime }$被设定为$C/8$以减少特征维数

• 定义一个时空注意图$A\in R^{N\times N}$作为相似矩阵，相似度矩阵中的元素A[i, j]是第i个键与第j个查询之间的相似度。对关键矩阵$K^{-T}$的转置和查询矩阵$Q^{-}$进行矩阵乘法运算，将每个元素除以√$C^{\prime }$，对每一列应用一个softmax函数生成注意图A。A的定义如下:
  

• 输出矩阵$Y^{-}\in R^{C\times N}$由值矩阵$V^{-}$与相似矩阵A的矩阵相乘计算得到:$Y^{-}=V^{-}A$

• 最后，$Y^{-}$被重塑为Y。

？为什么除以√c0

矩阵乘法结果被缩放为√$C^{\prime }$，以使其期望值不受$C^{\prime }$大值的影响

PAM

我们提出了一种PAM，通过聚合多尺度时空注意上下文来增强识别细节的能力。PAM通过结合不同尺度的注意时空语境生成多尺度注意特征。

输入：$X\in R^{C\times H\times W\times 2}$

输出：$Z\in R^{C\times H\times W\times 2}$

• 我们将双时间特征地图 $X^{(1)}$, $X^{(2)}$∈$R^{C\times H\times W}$的特征映射叠加到一个特征张量中$X\in R^{C\times H\times W\times 2}$
• 有四个平行的分支;每个分支将特征张量等分为s × s子区域，其中$s\in S$ $ S $=1,2,4,8定义了四个金字塔尺度。在s标度分支中，每个区域定义为$R_{s,i,j}∈R^{C×H /s×W /s×2}$, 1≤i,j≤s.
• 我们分别对四个分支使用了四个BAM。在每个金字塔分支中，我们分别对所有子区域$R_{s,i,j}$应用BAM,生成更新的残差特征张量$Y_s\in R^{C\times H\times W\times 2}$
• 将这些特征张量$Y_s,s\in S$拼接到一个卷积层(C, 1 × 1/1)中，得到最终的残差特征张量$Y\in R^{C\times H\times W\times 2}$
• 最后，我们将剩余张量Y和原始张量X相加，得到更新后的张量$Z\in R^{C\times H\times W\times 2}$

3.3 度量模块

深度度量学习是指训练网络学习从输入到嵌入空间的非线性变换，在这个变换中，相似样本的嵌入向量被鼓励更接近，而不同样本的嵌入向量被推离。基于深度度量学习的CD方法取得了领先的成绩。在这里，我们使用对比损失来鼓励每个不变的像素对（小距离的），每个变化的嵌入空间（大距离的）。

输入：$Z^{(1)}$,$Z^{(2)}$

• 首先通过双线性插值将每个特征图的大小调整为与输入的双时间图像相同的大小。

• 然后按像素计算调整尺寸后的特征地图之间的欧氏距离，生成距离地图$D\in R^{H_0\times W_0}$,

  其中H0、W0分别为输入图像的高度和宽度。

• 在训练阶段，使用对比损失来学习网络的参数，这样邻居被拉在一起，非邻居被推开

• 在测试阶段，通过固定阈值分割得到变化图P:

下标i，j分别表示高度和宽度的指标。θ是用来区分变化区域的固定阈值。在我们的工作中，θ被指定为1，也就是损失函数中定义的边际的一半。

3.4 损失层设计

？解决的问题

在大多数机器学习任务中，类分布高度不平衡的情况下，class不平衡问题很常见。对于遥感影像CD，变化样本和不变样本数量变化较大。在很多情况下，变化的像素只占所有像素的一小部分，这导致网络在训练阶段存在一定的偏差。

为了减少类不平衡的影响，我们设计了类敏感损失;即批平衡对比损失(BCL)。

给一批双时间样本$(X^{\ast (1)},X^{\ast (2)},M^{\ast },X^{\ast (1)},X^{\ast (2)}\in R^{B\times H_0\times W_0},M\ast \in R^{B\times H_0\times W_0})$,我们可以通过STANET得到一批距离地图$D^{\ast }\in R^{B\times H_0\times W_0}$，其中B为样品的批号。

$M^{\ast }$是一批二进制标号映射，其中0表示没有变化，1表示变化。BCL的定义如下:

下标b，i，j分别表示批数,高度和宽度的指标。参数化距离大于边界m的变化像素对对损失函数没有贡献。

在我们的工作中，m等于2。$n_u$,$n_c$分别为未改变像素对和改变像素对的个数。它们可以由对应类别的标签之和计算:

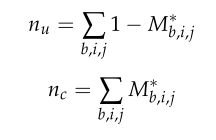
4 实现细节

4.1 指标

我们将精度(Pr)、召回率(Re)和F1-score (F1)作为评价指标。设$n_{ij}$为第i类预测为第j类的像素数，其中有$n_c$classes。我们计算:

4.2 LEVIR-CD数据集

我们将数据随机分成三部分:70%的样本用于训练，10%的样本用于验证，20%的样本用于测试。由于GPU的内存限制，我们将每个样本裁剪成16个256× 256大小的小补丁。

4.3 SZTAKI数据集

我们使用与其他比较方法相同的训练测试分裂标准。测试集由每个样本从左上角裁剪出大小为784× 448的patches组成。每个样本的剩余部分重叠裁剪成113× 113大小的小块作为训练数据。

4.4 训练细节

我们的模型在imagenet -pre- training ResNet-18模型上进行了微调，初始学习速率为$10^{-3}$。接下来，我们对前100个epoch保持相同的学习速率，并在剩下的100个epoch中将其线性衰减到0。我们使用批量大小为4的Adam求解器，β1为0.5，β2为0.99。我们应用随机翻转和随机旋转(−15◦∼15◦)的数据增强。

4.5 baseline比对

为了验证时空模块的有效性，我们设计了一种基线方法:

• Baseline: FCN-networks (BASE)及其改进变体与时空模块:
• Proposed 1: FCN-networks + BAM (BAM)
• Proposed 2: FCN-networks + PAM (PAM)。

所有比较都使用相同的超参数设置。

LEVIR-CD:一种新的遥感图像变化检测数据集

大型和具有挑战性的数据集对遥感应用非常重要。然而，在遥感图像CD中，我们注意到缺乏一个公共的、大规模的CD数据集，这阻碍了CD的研究，特别是开发基于深度学习的算法。因此，通过引入LEVIR-CD数据集，我们希望填补这一空白，并为评估CD算法提供更好的基准。

在这里，我们简要介绍三个CD数据集:

• SZTAKI AirChange Benchmark Set (SZTAKI)是一个包含13对光学航空影像的二值CD数据集;每个为952×640像素，分辨率约为1.5 m/像素。数据集按区域划分为三个集;即Szada, Tiszadob和Archive;它们分别包含7、5和1对图像。数据集考虑以下变化:新建建成区、建筑作业、造林、新耕地和建筑完成前的地基。
• Onera卫星变化检测数据集(OSCD)用于二值CD，收集24对多光谱卫星图像。在10m分辨率下，每个图像的大小约为600× 600。该数据集中于城市地区的变化(例如，城市增长和城市衰落)，而忽略了自然变化。
• 航空图像变化检测数据集(AICD)是一个合成的二进制CD数据集，包含100个模拟场景，每个场景从5个视点捕获，总共提供500张图像。每幅图像添加一种人为的变化目标(如建筑物、树木或浮雕)来生成图像对。因此，每个映像对中都有一个更改实例。