吴恩达机器学习python实现(6):SVM支持向量机(文末附完整代码)
所有的数据来源:链接:https://pan.baidu.com/s/1vTaw1n77xPPfKk23KEKARA
提取码:5gl2
1 Support Vector Machines
1.1 Prepare datasets
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb # 更好的可视化封装库
from scipy.io import loadmat
from sklearn import svm
'''
1.Prepare datasets
'''
mat = loadmat('data/ex6data1.mat')
print(mat.keys())
# dict_keys(['__header__', '__version__', '__globals__', 'X', 'y'])
X = mat['X']
y = mat['y']
'''大多数SVM的库会自动帮你添加额外的特征x0,所以无需手动添加。'''
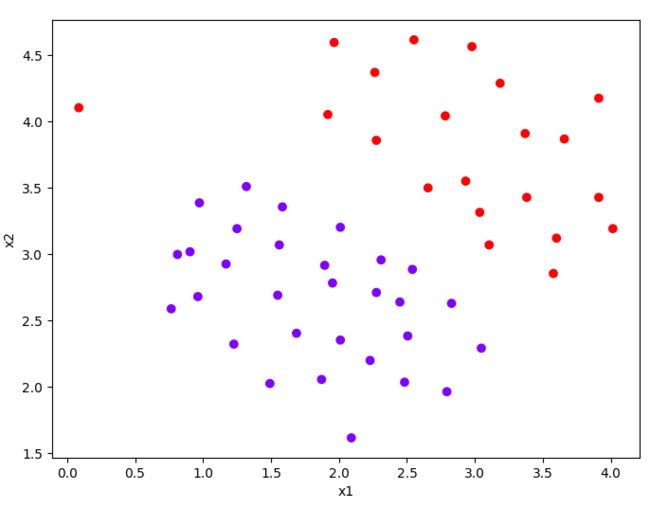
def plotData(X, y):
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y.flatten(), cmap='rainbow')
# c=list,设置cmap,根据label不一样,设置不一样的颜色
# c:色彩或颜色序列 camp:colormap(颜色表)
plt.xlabel('x1')
plt.ylabel('x2')
# plt.legend()
# plt.grid(True)
# # plt.show()
pass
# plotData(X, y)
接下来取一段范围,这段范围是根据已有数据的大小进行细微扩大,并且将其分成500段,通过meshgrid获得网格线,最终利用等高线图画出分界线
1.2 Decision Boundary
def plotBoundary(clf, X):
'''Plot Decision Boundary'''
x_min, x_max = X[:, 0].min() * 1.2, X[:, 0].max() * 1.1
y_min, y_max = X[:, 1].min() * 1.1, X[:, 1].max() * 1.1
# np.linspace(x_min, x_max, 500).shape---->(500, ) 500是样本数
# xx.shape, yy.shape ---->(500, 500) (500, 500)
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# model.predict:模型预测 (250000, )
# ravel()将多维数组转换为一维数组 xx.ravel().shape ----> (250000,1)
# np.c 中的c是column(列)的缩写,就是按列叠加两个矩阵,就是把两个矩阵左右组合,要求行数相等。
# np.c_[xx.ravel(), yy.ravel()].shape ----> (250000,2) 就是说建立了250000个样本
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z)
# 等高线得作用就是画出分隔得线
pass
通过调用sklearn中支持向量机的代码,来进行模型的拟合
models = [svm.SVC(C, kernel='linear') for C in [1, 100]]
# 支持向量机模型 (kernel:核函数选项,这里是线性核函数 , C:权重,这里取1和100)
# 线性核函数画的决策边界就是直线
clfs = [model.fit(X, y.ravel()) for model in models] # model.fit:拟合出模型
score = [model.score(X, y) for model in models] # [0.9803921568627451, 1.0]
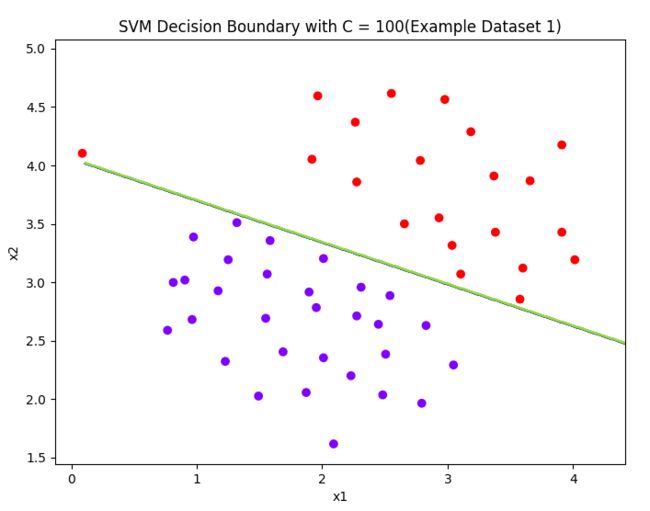
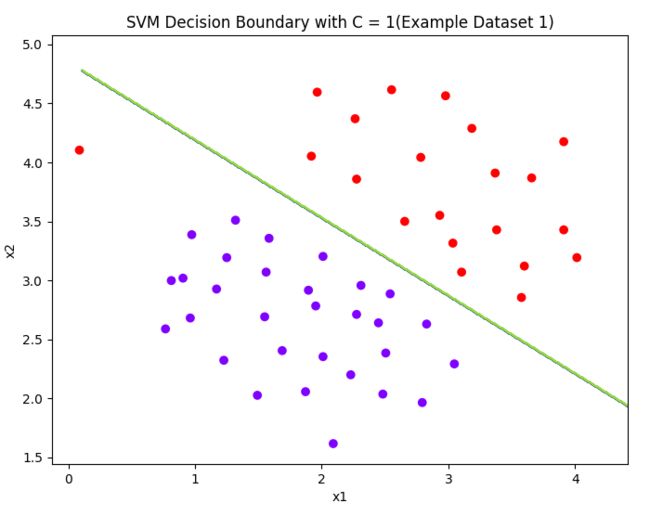
# title = ['SVM Decision Boundary with C = {}(Example Dataset 1)'.format(C) for C in [1, 100]]
def plot():
title = ['SVM Decision Boundary with C = {}(Example Dataset 1)'.format(C) for C in [1, 100]]
for model, title in zip(clfs, title):
# zip() 函数用于将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。
plt.figure(figsize=(8, 5))
plotData(X, y)
plotBoundary(model, X) # 用拟合好的模型(预测那些250000个样本),绘制决策边界
plt.title(title)
pass
pass
# plt.show()
A large C parameter tells the SVM to try to classify all the examples correctly.
C plays a rolesimilar to λ, where λ is the regularization parameter that we were using previously for logistic regression.
可以理解对误差的惩罚,惩罚大,则曲线分类精准。
1.2 SVM with Gaussian Kernels
当用SVM作非线性分类时,我们一般使用Gaussian Kernels。
K gaussian ( x ( i ) , x ( j ) ) = exp ( − ∥ x ( i ) − x ( j ) ∥ 2 2 σ 2 ) = exp ( − ∑ k = 1 ( x k ( i ) − x k ( j ) ) 2 2 σ 2 ) K_{\text {gaussian }}\left(x^{(i)}, x^{(j)}\right)=\exp \left(-\frac{\left\|x^{(i)}-x^{(j)}\right\|^{2}}{2 \sigma^{2}}\right)=\exp \left(-\frac{\sum_{k=1}\left(x_{k}^{(i)}-x_{k}^{(j)}\right)^{2}}{2 \sigma^{2}}\right) Kgaussian (x(i),x(j))=exp(−2σ2∥∥x(i)−x(j)∥∥2)=exp⎝⎜⎛−2σ2∑k=1(xk(i)−xk(j))2⎠⎟⎞
本文中使用其自带的即可。
def gaussKernel(x1, x2, sigma):
return np.exp(-(x1 - x2) ** 2).sum() / (2 * sigma ** 2)
a = gaussKernel(np.array([1, 2, 1]), np.array([0, 4, -1]), 2.) # 0.32465246735834974
# print(a)
1.2.1 Gaussian Kernel-Example Dataset2
mat = loadmat('data/ex6data2.mat')
x2 = mat['X']
y2 = mat['y']
plotData(x2, y2)
plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ktLdbJ8u-1622612399587)(C:/Users/DELL/AppData/Roaming/Typora/typora-user-images/image-20210601172524887.png)]
sigma = 0.1
gamma = np.power(sigma, -2)/2
'''
高斯核函数中的gamma越大,相当高斯函数中的σ越小,此时的分布曲线也就会越高越瘦。
高斯核函数中的gamma越小,相当高斯函数中的σ越大,此时的分布曲线也就越矮越胖,smoothly,higher bias, lower variance
'''
clf = svm.SVC(C=1, kernel='rbf', gamma=gamma)
model = clf.fit(x2, y2.flatten()) # kernel='rbf'表示支持向量机使用高斯核函数
# https://blog.csdn.net/guanyuqiu/article/details/85109441
# plotData(x2, y2)
# plotBoundary(model, x2)
# plt.show()
1.2.2 Gaussian Kernel-Example Dataset3
'''
Example Dataset3
'''
mat3 = loadmat('data/ex6data3.mat')
x3, y3 = mat3['X'], mat3['y']
Xval, yval = mat3['Xval'], mat3['yval']
plotData(x3, y3)
# plt.show()
Cvalues = (0.01, 0.03, 0.1, 0.3, 1., 3., 10., 30.) # 权重C的候选值
sigmavalues = Cvalues # 核函数参数的候选值
best_pair, best_score = (0, 0), 0 # 最佳的(C,sigma)权值 ,决定系数(R2)
# 寻找最佳的权值(C,sigma)
for C in Cvalues:
for sigma in sigmavalues:
gamma = np.power(sigma, -2.) / 2
model = svm.SVC(C=C, kernel='rbf', gamma=gamma) # 使用核函数的支持向量机
model.fit(x3, y3.flatten()) # 拟合出模型
this_score = model.score(Xval, yval) # 利用交叉验证集来选择最合适的权重
'''
model.score函数的返回值是决定系数,也称R2。
可以测度回归直线对样本数据的拟合程度,决定系数的取值在0到1之间,
决定系数越高,模型的拟合效果越好,即模型解释因变量的能力越强。
'''
# 选择拟合得最好得权重值
if this_score > best_score:
best_score = this_score
best_pair = (C, sigma)
pass
pass
print('最优(C, sigma)权值:', best_pair, '决定系数:', best_score)
# 最优(C, sigma)权值: (1.0, 0.1) 决定系数: 0.965
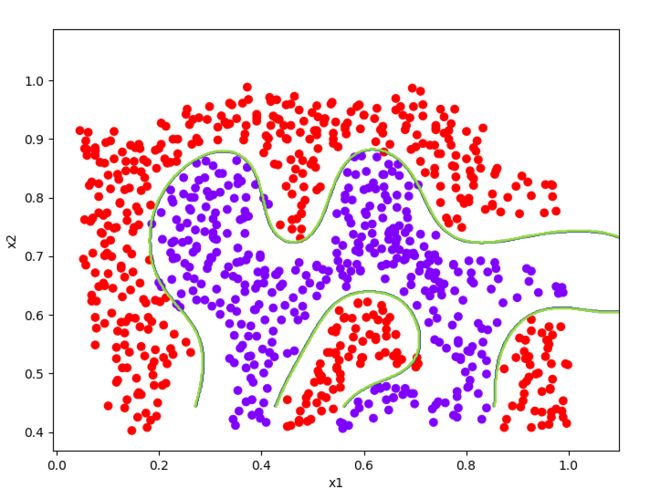
model = svm.SVC(1, kernel='rbf', gamma=np.power(0.1, -2.) / 2)
# 用确定好的权重再重新声明一次支持向量机
model.fit(x3, y3.flatten())
plotData(x3, y3)
plotBoundary(model, x3)
# plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zODc0dOu-1622612399590)(C:/Users/DELL/AppData/Roaming/Typora/typora-user-images/image-20210601224239696.png)]
SVM中的score的作用:
2 Spam Classfication
邮件分类这一块就偷一下懒拉,给大家看看代码
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
from sklearn import svm
import pandas as pd
import re # regular expression for e-mail processing
# 这是一个可用的英文分词算法(Porter stemmer)
from stemming.porter2 import stem
# 这个英文算法似乎更符合作业里面所用的代码,与上面效果差不多
import nltk, nltk.stem.porter
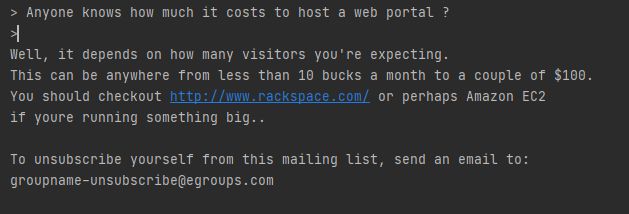
with open('data/emailSample1.txt', 'r') as f:
email = f.read()
pass
print(email)
# 我们可以做如下处理:
# 1. Lower-casing: 把整封邮件转化为小写。
# 2. Stripping HTML: 移除所有HTML标签,只保留内容。
# 3. Normalizing URLs: 将所有的URL替换为字符串 “httpaddr”.
# 4. Normalizing Email Addresses: 所有的地址替换为 “emailaddr”
# 5. Normalizing Dollars: 所有dollar符号($)替换为“dollar”.
# 6. Normalizing Numbers: 所有数字替换为“number”
# 7. Word Stemming(词干提取): 将所有单词还原为词源。
# 例如,“discount”, “discounts”, “discounted” and “discounting”都替换为“discount”。
# 8. Removal of non-words: 移除所有非文字类型,所有的空格(tabs, newlines, spaces)调整为一个空格.
def processEmail(email):
'''除了Word Stemming, Removal of non-words之外所有的操作'''
email = email.lower()
email = re.sub('<[^<>]>', '', email) # 匹配<开头,然后所有不是< ,> 的内容,知道>结尾,相当于匹配<...>
email = re.sub('(http|https)://[^\s]*', 'httpaddr', email) # 匹配//后面不是空白字符的内容,遇到空白字符则停止
email = re.sub('[^\s]+@[^\s]+', 'emailaddr', email)
email = re.sub('[\$]+', 'dollar', email)
email = re.sub('[\d]+', 'number', email)
return email
def email2TokenList(email):
"""预处理数据,返回一个干净的单词列表"""
# I'll use the NLTK stemmer because it more accurately duplicates the
# performance of the OCTAVE implementation in the assignment
stemmer = nltk.stem.porter.PorterStemmer()
email = processEmail(email)
# 将邮件分割为单个单词,re.split() 可以设置多种分隔符
tokens = re.split('[ \@\$\/\#\.\-\:\&\*\+\=\[\]\?\!\(\)\{\}\,\'\"\>\_\<\;\%]', email)
# 遍历每个分割出来的内容
tokenlist = []
for token in tokens:
# 删除任何非字母数字的字符
token = re.sub('[^a-zA-Z0-9]', '', token)
# Use the Porter stemmer to 提取词根
stemmed = stemmer.stem(token)
# 去除空字符串‘’,里面不含任何字符
if not len(token):
continue
tokenlist.append(stemmed)
return tokenlist
# 在对邮件进行预处理之后,我们有一个处理后的单词列表。
# 下一步是选择我们想在分类器中使用哪些词,我们需要去除哪些词。
# 我们有一个词汇表vocab.txt,里面存储了在实际中经常使用的单词,共1899个。
# 我们要算出处理后的email中含有多少vocab.txt中的单词,并返回在vocab.txt中的index,
# 这就我们想要的训练单词的索引。
def email2VocanIndices(email, vocab):
'''提取存在单词的索引'''
token = email2TokenList(email)
index = [i for i in range(len(vocab)) if vocab[i] in token]
return index
def email2FeatureVector(email):
'''
将email转化为词向量,n是vocab的长度。存在单词的相应位置的值置为1,其余为0
:param email:
:return:
'''
df = pd.read_table('data/vocab.txt', names=['words'])
vocab = np.array(df) # return array
vector = np.zeros(len(vocab)) # init vector
vocab_indices = email2VocanIndices(email, vocab) # 返回含有单词的索引
# 将有单词的索引值置为1
for i in vocab_indices:
vector[i] = 1
pass
return vector
vector = email2FeatureVector(email)
print('length of vector = {}\nnum of non-zero = {}'.format(len(vector), int(vector.sum())))
# Training set
mat1 = loadmat('data/spamTrain.mat')
X, y = mat1['X'], mat1['y']
# Test set
mat2 = loadmat('data/spamTest.mat')
Xtest, ytest = mat2['Xtest'], mat2['ytest']
clf = svm.SVC(C=0.1, kernel='linear')
clf.fit(X, y)
predTrain = clf.score(X, y)
predTest = clf.score(Xtest, ytest)
print(predTrain, predTest)
# 0.99825
附完整代码:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb # 更好的可视化封装库
from scipy.io import loadmat
from sklearn import svm
'''
1.Prepare datasets
'''
mat = loadmat('data/ex6data1.mat')
print(mat.keys())
# dict_keys(['__header__', '__version__', '__globals__', 'X', 'y'])
X = mat['X']
y = mat['y']
'''大多数SVM的库会自动帮你添加额外的特征x0,所以无需手动添加。'''
def plotData(X, y):
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y.flatten(), cmap='rainbow')
# c=list,设置cmap,根据label不一样,设置不一样的颜色
# c:色彩或颜色序列 camp:colormap(颜色表)
plt.xlabel('x1')
plt.ylabel('x2')
# plt.legend()
# plt.grid(True)
# # plt.show()
pass
# plotData(X, y)
def plotBoundary(clf, X):
'''Plot Decision Boundary'''
x_min, x_max = X[:, 0].min() * 1.2, X[:, 0].max() * 1.1
y_min, y_max = X[:, 1].min() * 1.1, X[:, 1].max() * 1.1
# np.linspace(x_min, x_max, 500).shape---->(500, ) 500是样本数
# xx.shape, yy.shape ---->(500, 500) (500, 500)
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# model.predict:模型预测 (250000, )
# ravel()将多维数组转换为一维数组 xx.ravel().shape ----> (250000,1)
# np.c 中的c是column(列)的缩写,就是按列叠加两个矩阵,就是把两个矩阵左右组合,要求行数相等。
# np.c_[xx.ravel(), yy.ravel()].shape ----> (250000,2) 就是说建立了250000个样本
Z = Z.reshape(xx.shape)
plt.contour(xx, yy, Z)
# 等高线得作用就是画出分隔得线
pass
models = [svm.SVC(C, kernel='linear') for C in [1, 100]]
# 支持向量机模型 (kernel:核函数选项,这里是线性核函数 , C:权重,这里取1和100)
# 线性核函数画的决策边界就是直线
clfs = [model.fit(X, y.ravel()) for model in models] # model.fit:拟合出模型
score = [model.score(X, y) for model in models] # [0.9803921568627451, 1.0]
# title = ['SVM Decision Boundary with C = {}(Example Dataset 1)'.format(C) for C in [1, 100]]
def plot():
title = ['SVM Decision Boundary with C = {}(Example Dataset 1)'.format(C) for C in [1, 100]]
for model, title in zip(clfs, title):
# zip() 函数用于将可迭代的对象作为参数,将对象中对应的元素打包成一个个元组,然后返回由这些元组组成的列表。
plt.figure(figsize=(8, 5))
plotData(X, y)
plotBoundary(model, X) # 用拟合好的模型(预测那些250000个样本),绘制决策边界
plt.title(title)
pass
pass
# plt.show()
'''
2.SVM with Gaussian Kernels
'''
def gaussKernel(x1, x2, sigma):
return np.exp(-(x1 - x2) ** 2).sum() / (2 * sigma ** 2)
a = gaussKernel(np.array([1, 2, 1]), np.array([0, 4, -1]), 2.) # 0.32465246735834974
# print(a)
'''
Example Dataset 2
'''
mat = loadmat('data/ex6data2.mat')
x2 = mat['X']
y2 = mat['y']
plotData(x2, y2)
plt.show()
sigma = 0.1
gamma = np.power(sigma, -2)/2
'''
高斯核函数中的gamma越大,相当高斯函数中的σ越小,此时的分布曲线也就会越高越瘦。
高斯核函数中的gamma越小,相当高斯函数中的σ越大,此时的分布曲线也就越矮越胖,smoothly,higher bias, lower variance
'''
clf = svm.SVC(C=1, kernel='rbf', gamma=gamma)
model = clf.fit(x2, y2.flatten()) # kernel='rbf'表示支持向量机使用高斯核函数
# https://blog.csdn.net/guanyuqiu/article/details/85109441
# plotData(x2, y2)
# plotBoundary(model, x2)
# plt.show()
'''
Example Dataset3
'''
mat3 = loadmat('data/ex6data3.mat')
x3, y3 = mat3['X'], mat3['y']
Xval, yval = mat3['Xval'], mat3['yval']
plotData(x3, y3)
# plt.show()
Cvalues = (0.01, 0.03, 0.1, 0.3, 1., 3., 10., 30.) # 权重C的候选值
sigmavalues = Cvalues # 核函数参数的候选值
best_pair, best_score = (0, 0), 0 # 最佳的(C,sigma)权值 ,决定系数(R2)
# 寻找最佳的权值(C,sigma)
for C in Cvalues:
for sigma in sigmavalues:
gamma = np.power(sigma, -2.) / 2
model = svm.SVC(C=C, kernel='rbf', gamma=gamma) # 使用核函数的支持向量机
model.fit(x3, y3.flatten()) # 拟合出模型
this_score = model.score(Xval, yval) # 利用交叉验证集来选择最合适的权重
'''
model.score函数的返回值是决定系数,也称R2。
可以测度回归直线对样本数据的拟合程度,决定系数的取值在0到1之间,
决定系数越高,模型的拟合效果越好,即模型解释因变量的能力越强。
'''
# 选择拟合得最好得权重值
if this_score > best_score:
best_score = this_score
best_pair = (C, sigma)
pass
pass
print('最优(C, sigma)权值:', best_pair, '决定系数:', best_score)
# 最优(C, sigma)权值: (1.0, 0.1) 决定系数: 0.965
model = svm.SVC(1, kernel='rbf', gamma=np.power(0.1, -2.) / 2)
# 用确定好的权重再重新声明一次支持向量机
model.fit(x3, y3.flatten())
plotData(x3, y3)
plotBoundary(model, x3)
# plt.show()
参考链接:https://blog.csdn.net/Cowry5/article/details/80465922