模糊聚类

1、模糊聚类的matlab实现

1.1、代码

%模糊控制器设计
a=newfis('fuzzf');%newfis：创建并返回一个新的FIS(模糊推理)系统

%输入1：变量e
f1=2; 
a=addvar(a,'input','e',[-8*f1,5*f1]);%向模糊推理系统中添加语言变量
%此处添加了一个变量e,取值范围为[-16,10]    

%添加隶属函数
%添加 e 的模糊语言变量，即向模糊推理系统的语言变量添加隶属度函数
a=addmf(a,'input',1,'NB','zmf',[-8*f1,-3*f1]);%zmf:z型隶属度函数。          
%添加 e 的模糊语言变量的隶属度函数（z型）
a=addmf(a,'input',1,'NM','trimf',[-7*f1,-4*f1,-1*f1]);%trimf：三角形隶属度函数。左边点，中间点，右边点      
a=addmf(a,'input',1,'NS','trimf',[-5*f1,-2*f1,1*f1]); 
a=addmf(a,'input',1,'Z','trimf',[-2*f1,0,2*f1]); 
a=addmf(a,'input',1,'PS','gaussmf',[-1*f1,2*f1]);%gaussmf:高斯隶属度函数
a=addmf(a,'input',1,'PM','trimf',[0,1*f1,3*f1]);
a=addmf(a,'input',1,'PB','smf',[1*f1,5*f1]); %smf:s型隶属度函数

%输入2：变量ec
f2=1;
a=addvar(a,'input','ec',[-14*f2,9*f2]);                   
 %添加 ec 的模糊语言变量
a=addmf(a,'input',2,'NB','zmf',[-14*f2,-9*f2]); 
a=addmf(a,'input',2,'NM','trapmf',[-13*f2,-11*f2,-9*f2,-7*f2]);%trapmf：梯形隶属度函数
a=addmf(a,'input',2,'NS','trimf',[-11*f2,-8*f2,-5*f2]);
a=addmf(a,'input',2,'Z','trimf',[-8*f2,-4*f2,0]);
a=addmf(a,'input',2,'PS','trimf',[-1*f2,1*f2,3*f2]);
a=addmf(a,'input',2,'PM','trapmf',[2*f2,4*f2,6*f2,8*f2]);
a=addmf(a,'input',2,'PB','smf',[5*f2,9*f2]); 

%控制变量的输出
f3=2;
a=addvar(a,'output','u',[-5*f3,5*f3]);                 
%添加 u 的模糊语言变量
a=addmf(a,'output',1,'NB','zmf',[-5*f3,-1*f3]); 
a=addmf(a,'output',1,'NM','trimf',[-4*f3,-2*f3,0]);
a=addmf(a,'output',1,'NS','trimf',[-3*f3,-1*f3,1*f3]);
a=addmf(a,'output',1,'Z','trimf',[-2*f3,0,2*f3]);
a=addmf(a,'output',1,'PS','trimf',[-1*f3,3*f3,5*f3]);
a=addmf(a,'output',1,'PM','trimf',[0,2*f3,5*f3]);
a=addmf(a,'output',1,'PB','smf',[1*f3,5*f3]);

%规则库:编辑模糊规则，后俩个数分别是规则权重和AND(1) OR(2)选项
rulelist=[1 1 1 1 1;             
               1 2 1 1 1;
               1 3 1 1 1;
               1 4 2 1 1;
               1 5 2 1 2;
               1 6 3 1 1;
               1 7 4 1 1;
               
               2 1 1 1 1;
               2 2 2 1 1;
               2 3 2 1 2;
               2 4 3 1 1;
               2 5 3 1 1;
               2 6 3 1 2;
               2 7 5 1 2;
               
               3 1 1 1 1;
               3 2 2 1 1;
               3 3 2 1 1;
               3 4 4 1 1;
               3 5 3 1 1;
               3 6 6 1 1;
               3 7 5 1 1;
               
               4 1 1 1 1;
               4 2 4 1 1;
               4 3 2 1 1;
               4 4 3 1 2;
               4 5 3 1 1;
               4 6 4 1 1;
               4 7 7 1 1;
               
               5 1 1 1 1;
               5 2 3 1 2;
               5 3 2 1 1;
               5 4 7 1 2;
               5 5 3 1 1;
               5 6 3 1 1;
               5 7 5 1 1;];
                         
a=addrule(a,rulelist);%添加模糊规则函数
showrule(a);%显示模糊规则函数
a1=setfis(a,'DefuzzMethod','mom');%设置解模糊方法,mom:平均最大隶属度法
writefis(a1,'fuzzf');%保存模糊系统
a2=readfis('fuzzf');%从磁盘读出保存的模糊系统
disp('fuzzy Controller table:e=[-16,+10],ec=[-14,+9]');%显示矩阵和数组内容

%推理
Ulist=zeros(7,7);%全零矩阵
for i=1:7
       for j=1:7
           e(i)=-6+i;
           ec(j)=-9+j;
           Ulist(i,j)=evalfis([e(i),ec(j)],a2);%完成模糊推理计算
       end
   end
%   Ulist=ceil(Ulist) %朝正无穷方向取整
   Ulist %朝正无穷方向取整 
   
%画出模糊系统
figure(1); plotfis(a2);%绘制模糊推理系统的推理过程结构框图。  
figure(2);plotmf(a,'input',1);%绘制语言变量所有语言值的隶属度函数曲线
figure(3);plotmf(a,'input',2);
figure(4);plotmf(a,'output',1);

1.2、运行结果

分析：首先输出的35行是代码中编辑的35条模糊规则，保存于rulelist中。此处的规则库rulelist有五列，分别代表：第一个输入的第几个隶属度函数、第二个输入的第几个隶属度函数、输出的第几个隶属度函数、规则权重以及之间的关系（AND用1表示，OR用2表示）。以”fuzzy Controller”为开头的输出是通过disp函数输出的，此处告诉了我们两个输入的取值范围。最后的输出是完成模糊推理计算之后的结果Ulist。

分析：由图可以得知，这个模糊推理系统的名字为fuzzf，它有两个输入（e和ec），一个输出（u），共构造了35个规则。两个输入和一个输出分别有7个隶属度函数。根据代码a1=setfis(a,‘DefuzzMethod’,‘mom’)，可知采用的解模糊方法为平均最大隶属度法（mom）。

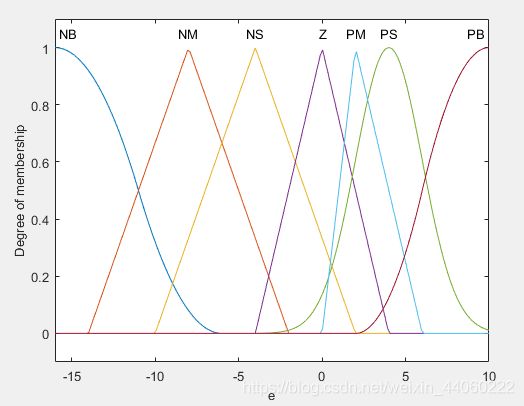
分析：第一个输入e的所有隶属度函数曲线

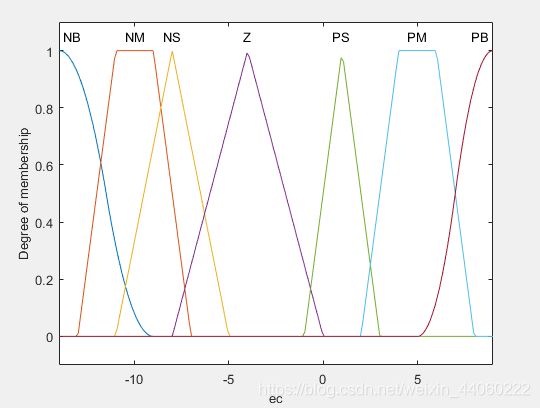
分析：第二个输入ec的所有隶属度函数曲线

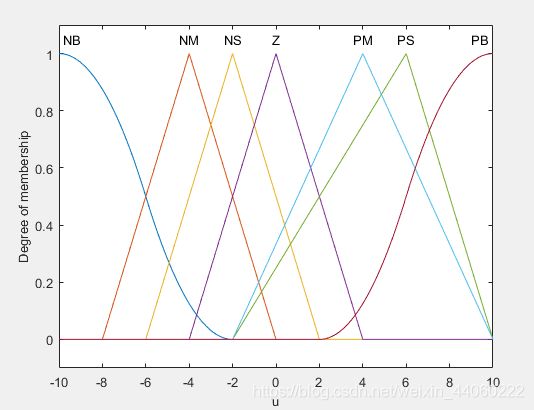
分析：输出u的所有隶属度函数曲线

2、结论

2.1、模糊计算的流程

• 计算控制变量：输入、输出
• 模糊量化处理：将观测到的数值集合转换成模糊集合
• 构建模糊控制规则
• 解模糊化处理（即非模糊化处理）
• 模糊推理

2.2、模糊计算的优缺点

2.2.1、优点

• 模糊逻辑采用隶属度来表达，更适合描述实际生活中陈述的不精确性。
• 模糊逻辑为参数调整提供了一种重要的工具。

2.2.2、缺点

• 当系统非常复杂时，传统的模糊计算难于保证规则与隶属度是充足、有效且低消耗的。此时可以与智能算法相结合。

对于模糊聚类来说，matlab中含有很多已分封好的方法，实现较为方便。