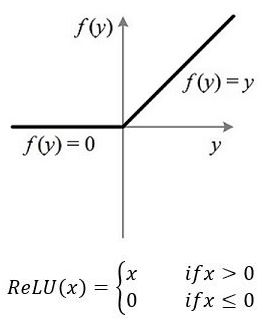深度学习入门--斋藤康毅 总结
一. 本书学习趋势
从浅至深,从易到难。
1.从感知机出发为我们学习神经网络奠定基础
2.介绍简单的基于随机梯度下降法(SGD) 的神经网络
3.稍显复杂一些的卷积神经网络(CNN)
二.感知机
2.1
感知机是由美国学者FrankRosenblatt在1957年提出来的。感知机是作为神经网络(深度学习)的起源的算法。因此,学习感知机的构造也就是学习通向神经网络和深度学习的一种重要思想。
感知机接收多个输入信号,输出一个信号。这里所说的“信号”可以想象成电流或河流那样具备“流动性”的东西。像电流流过导线,向前方输送电子一样,感知机的信号也会形成流,向前方输送信息。但是,和实际的电流不同的是,感知机的信号只有“流/不流”(1/0)两种取值。这里我们认为0对应“不传递信号”, 1对应“传递信号”。
下图1就是一个接收两个输入信号的感知机的例子。
![]()
图1 两个输入的感知机
x1、 x2是输入信号,y是输出信号, w1、 w2是权重(w是weight的首字母)。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时,会被分别乘以固定的权重(w1x1、 w2x2)。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出1。这也称为“神经元被激活” 。这里将这个界限值称为阈值,用符号θ表示。
感知机的运行原理只有这些!把上述内容用数学式来表示,就是下面这个式子(1)。
感知机的多个输入信号都有各自固有的权重,这些权重发挥着控制各个信号的重要性的作用。也就是说,权重越大,对应该权重的信号的重要性就越高。
通过控制单层感知机的权重,我们能够实现与们,或门,与非门。
但要实现异或门,通过单层感知机是难以实现的。
因此我们引入多层感知机的概念。
定义:叠加了多层的感知机就是多层感知机。也就是说要通过两层权重的作用。
小结:
1. 感知机是具有输入和输出的算法。给定一组输入后,将输出一组输出(输入数不一定等于输出数)
2. 感知机将权重和偏置设定为参数
3. 异或门无法通过单层感知机表示,但能利用2层感知机表示
4.单层感知机只能表示线性空间,而多层感知机可以表示非线性空间
5.多层感知机理论上能表示计算机
三. 神经网络
神经网络是一种三层结构的网络分别是:输入层,中间层(隐藏层),输出层。
这里的中间层通常不止一层。如下图。
![]()
对于基础的全加神经网络,前一层的每个神经元都要通过权重作用于下一层的每一个神经网络(有同学可能会疑惑为什么前一层的每个神经元都要作用于后一个的每一个神经元呢?其实这并不影响,因为有权重的存在,如果前后两个神经元连接的权重为0,就相当于不连接,所以每一个都连接会帮助通过权重实际是在控制后续的学习过程)
那么前一层神经元穿过来的数据通过权重和偏置作用并进行累加后到达下一层神经元后,还将会有激活函数的作用。通过激活函数作用后,再传递给下一层的神经元。
常用的激活函数:
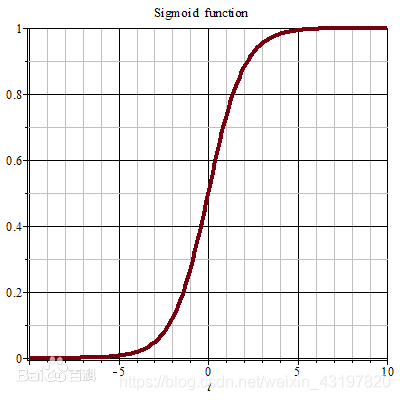
1. sigmoid函数
特点:值始终小于。
2. ReLU函数
从上图不难看出,ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变,这种操作被成为单侧抑制。可别小看这个简单的操作,正因为有了这单侧抑制,才使得神经网络中的神经元也具有了稀疏激活性。尤其体现在深度神经网络模型(如CNN)中,当模型增加N层之后,理论上ReLU神经元的激活率将降低2的N次方倍。这里或许有童鞋会问:ReLU的函数图像为什么一定要长这样?反过来,或者朝下延伸行不行?其实还不一定要长这样。只要能起到单侧抑制的作用,无论是镜面翻转还是180度翻转,最终神经元的输出也只是相当于加上了一个常数项系数,并不影响模型的训练结果。之所以这样定,或许是为了契合生物学角度,便于我们理解吧。
那么问题来了:这种稀疏性有何作用?换句话说,我们为什么需要让神经元稀疏?不妨举栗子来说明。当看名侦探柯南的时候,我们可以根据故事情节进行思考和推理,这时用到的是我们的大脑左半球;而当看蒙面唱将时,我们可以跟着歌手一起哼唱,这时用到的则是我们的右半球。左半球侧重理性思维,而右半球侧重感性思维。也就是说,当我们在进行运算或者欣赏时,都会有一部分神经元处于激活或是抑制状态,可以说是各司其职。再比如,生病了去医院看病,检查报告里面上百项指标,但跟病情相关的通常只有那么几个。与之类似,当训练一个深度分类模型的时候,和目标相关的特征往往也就那么几个,因此通过ReLU实现稀疏后的模型能够更好地挖掘相关特征,拟合训练数据。
此外,相比于其它激活函数来说,ReLU有以下优势:对于线性函数而言,ReLU的表达能力更强,尤其体现在深度网络中;而对于非线性函数而言,ReLU由于非负区间的梯度为常数,因此不存在梯度消失问题(Vanishing Gradient Problem),使得模型的收敛速度维持在一个稳定状态。这里稍微描述一下什么是梯度消失问题:当梯度小于1时,预测值与真实值之间的误差每传播一层会衰减一次,如果在深层模型中使用sigmoid作为激活函数,这种现象尤为明显,将导致模型收敛停滞不前。
通过中间层函数的作用后,我们怎样输出呢?
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出的激活函数。一般而言,回归问题用恒等函数,分类问题softmax函数。
![]()
通过softmax函数,能让输出值的和等于1,这样就能把输出看作一种概率了。
总结一下简单的神经网络。
输入层 ---->中间层(sigmoid函数,ReLU函数) ---->输出层(恒等函数,softmax函数)
几种处理方法:
正规化: 把数据限定到某个范围内的处理称为正规化。
预处理:对神经网络的输入数据进行某种既定的转换称为预处理。
数据白化:将数据整体的分布形状均匀化的方法
批处理:将多个数据打包处理。作用:缩短处理时间。原因:大多数处理数值计算的库都进行了能够高效处理大型数组运算的最优化。
四. 神经网络的学习
神经网络的特征就是可以从数据中学习。
所谓“从数据中学习”指可以由数据自动决定权重参数的值。
在神经网络的学习中,以损失函数为基准,学习的目的就是找出能使它的值达到最小的权重参数。
数据是机器学习的核心。
泛化能力是指处理未被观察过的数据的能力。获得泛化能力是机器学习的终极目标。
损失函数:
损失函数是表示神经网络性能的“恶劣程度”的指标,即当前的神经网络对监督数据在多大程度上不拟合,在多大程度上不一致。
这个损失函数可以使用任意函数,但一般用均方误差和交叉熵误差等。
均方误差:书P85
交叉熵误差:书P87
梯度法:
梯度法的数学表达式如下:
η表示更新量,在神经网络的学习中,称为学习率( learningrate)。学习率决定在一次学习中,应该学习多少,以及在多大程度上更新参数。
学习率需要事先确定为某个值,比如0.01或0.001。一般而言,这个值过大或过小,都无法抵达一个“好的位置”。在神经网络的学习中,一般会一边改变学习率的值,一边确认学习是否正确进行了。
学习率过大的话,会发散成一个很大的值;反过来,学习率过小的话,基本上没怎么更新就结束了。也就是说,设定合适的学习率是一个很重要的问题。
注:像学习率这样的参数称为超参数。这是一种和神经网络的参数(权重和偏置)性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的,学习率这样的超参数则是人工设定的。一般来说,超参数需要尝试多个值,以便找到一种可以使学习顺利进行的设定。
神经网络的梯度计算
神经网络的学习训练过程也是通过求梯度来一步步求得最优参数值的。这里的梯度指损失函数关于权重参数的梯度。比如,有一个只有一个形状为2 × 3的权重W的神经网络,损失函数用L表示。此时,梯度的数学式表示如下所示。
![]()
![]()
求出神经网络的梯度后,接下来只需根据梯度法,更新权重参数即可。
神经网络的全貌图:
前提
神经网络中有合适的权重和偏置,调整权重和偏置以便拟合训练数据的过程称为学习。神经网络的学习分为下面四个步骤。
步骤1 (mini-batch)
从训练数据中随机选择一部分数据
步骤2 (计算梯度)
计算损失函数关于各个权重参数的梯度
步骤3 (更新参数)
将权重参数沿梯度方向进行微小的更新
步骤3 (重复)
重复步骤1,步骤2,步骤3..
通常计算梯度可以用数值微分法或反向传播法。数值微分法运行速度慢,反向传播法运行速度相对快很多。反向传播法通过计算图的形式展示。
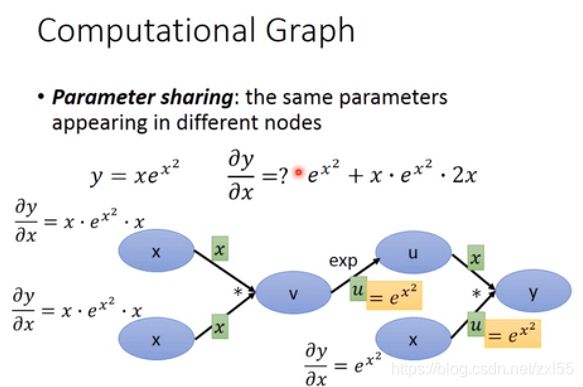
计算图
通过将神经网络的组成元素实现为层,可以高效地计算梯度(反向传播法)
通过比较数值微分和误差反向传播法的结果,可以确认误差反向传播法的实现是否正确(梯度确认)
五. 与学习相关的技巧
5.1 参数的更新
神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题,解决这个问题的过程称为最优化。
一些常用的方法:
1. SGD (随机梯度下降法)
2. Momentum
3. AdaGrad
4. Adam
5.2 权重的初始值
1. 不能将权重初始值设为0,不能将权重初始值设为一样的值,必须随机生成初始值。
2. Xavier 初始值:如果前一层的节点数为n, 则初始值使用标准差为1/sqrt(n)的高斯分布。
Xavier初始值是以激活函数是线性函数为前提而推导出来的。因为sigmoid函数和tanh函数左右堆成,且中央附近可以视为线性函数,所以适合使用Xavier初始值。但不适用与ReLU函数。
3. He 初始值: 当前一层的节点数为n时,He初始值使用标准差为sqrt(2/n)的高斯分布。适用于ReLU函数。
5.3 Batch Normalization
思路:调整各层的激活值分布使其拥有适当的广度。为此,要向神经网络中插入对数据分布进行正规化的层,即Batch Normalization层。
优点:
1. 可以使学习快速进行(可以增大学习率)
2. 不那么依赖初始值(对于初始值不用那么神经质)
3. 抑制过拟合(降低Dropout的必要性)
5.4 正则化
5.4.1 过拟合
发生过拟合的原因,主要有以下两个:
1. 模型拥有大量参数,表现力强
2. 训练数据小
抑制过拟合的方法:
1. 权值衰减
2.Dropout
6. 卷积神经网络(CNN)
整体结构:
CNN和之前介绍的神经网络一样,可以像乐高积木一样通过组装层来构建。不过CNN中新出现了卷积层(Convolution层)和池化层(Pooling层)..
之前介绍的神经网络中,相邻层的所有神经元之间都有连接,这称为全连接。
池化层:通常会缩小空间大小。Max池化层,Average池化层等。
使用im2col(image to colum)函数可以简单高效地实现卷积层和池化层。
具有代表的CNN
1.LeNet
2.AlexNet
7. 深度学习
1. 加深学习
2. 提高识别精度的技术和线索: 集成学习, 学习衰减率, Data Augmentation(数据扩充)
尤其是Data Augmentation 虽然方法简单,但在提高识别精度上效果显著。
3. ImageNet
4. VGG
5. GooLeNet
5. ResNet