机器学习（周志华） 第十三章半监督学习

关于周志华老师的《机器学习》这本书的学习笔记
记录学习过程
本博客记录Chapter13

1 半标记样本

我们有训练样本集$D_l=\{(x_1,y_1),(x_2，y_2),\cdots ,(x_l,y_l)\}$ ， 这$l$个样本的类别标记己知，称为“有标记” (labeled)样本；此外，还有$D_u=\{x_{l+1},x_{l+2},\cdots ,x_{l+u}\},l<<u$，这$u$个样本的类别标记未知，称为“未标记” (unlabeled)样本。若直接使用传统监督学习技术，则仅有$D_l$能用于构建模型，$D_u$所包含的信息被浪费了。另一方面，若$D_l$较小，则由于训练的样本不足，学得模型的泛化能力往往不佳。

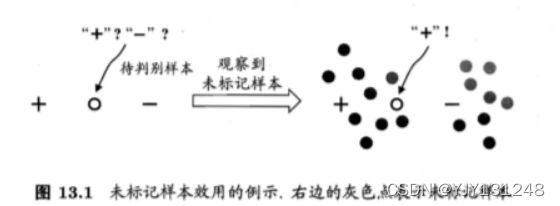
但我们仍然可以使用未标记样本。事实上，未标记样本虽然没有直接包含标记信息，但若它们与有标记样本是从同样的数据源独立同分布采样而来，则他们所包含的关于数据分布的信息对建立模型大有裨益。如下图，若能观察到图中的未标记样本，则能有把握地判断该例为正例。

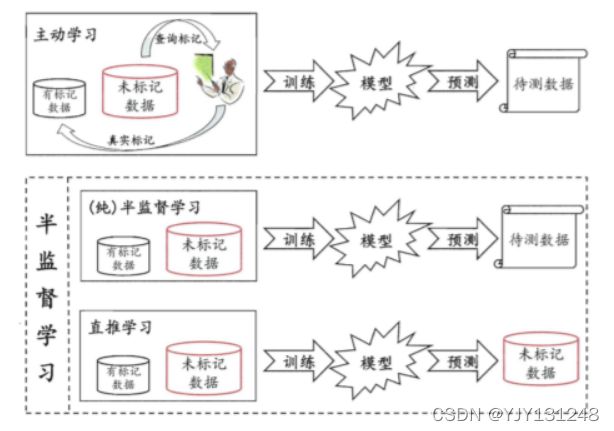
由上面的介绍，我们引入半监督学习的概念： 让学习器不依赖外界交互、自动地利用未标记样本来提升学习性能。 现实中，半监督学习的需求也很强烈。因为我们往往能较为容易地收集到大量未标记样本，而获取“标记”却要耗费大量人力、物力。半监督学习提供了一条利用“廉价”地未标记样本的途径。

要利用未标记样本，必然要做一些将未标记样本所揭示的数据分布信息与类别标记相联系的假设。如：

• 聚类假设：如图13.1；假设数据存在簇结构，同一个簇的样本属于同一个类别。
• 流形假设：假设数据分布在一个流形结构，邻近的样本拥有相似的输出值。

上述两类假设本质都是：相似的样本拥有相似的输出。

---

半监督学习可以进一步分类为：

• 纯半监督学习：假定训练数据中的未标记样本并非待预测的数据；即纯半监督学习是基于“开放世界”假设，希望学到的模型可以适用于训练过程中未观察到的未标记数据；
• 直推学习：假定学习过程中所考虑的未标记样本是待预测数据；基于“封闭世界”假设，试图对学习过程中观察到的未标记数据进行预测。

2 生成式方法

生成式方法（generative methods）：直接基于生成式模型的方法；假设所有的数据（无论是否有标记）都是 由同一个潜在的模型“生成” 的。

给定样本$x$，其真实类别标记为$y\in Y$，其中$Y=\{1,2,\cdots ,N\}$为所有可能的类别。假设样本由高斯混合模型生成，且每个类别对应一个高斯混合成分，即数据样本基于下列概率密度生成：
$$p(x)=\sum _{i=1}^N{\alpha }_i\cdot p(x|{\mu }_i,{\sum }_k)$$
其中，混合系数${\alpha }_i\ge 0，{\sum }_{i=1}^N{\alpha }_i=1$；

令$f(x)\in Y$表示模型$f$对$x$的预测标记，$\Theta \in \{1,2,\cdots ,N\}$表示样本$x$隶属的高斯混合成分。由最大化后验概率可知：
$$\begin{array}{rl}f(x)& ={\mathrm{argmax}}_{j\in Y}p(y=j|x)\\ & ={\mathrm{argmax}}_{j\in Y}\sum _{i=1}^{N}p(y=j,\Theta =i|x)\\ & ={\mathrm{argmax}}_{j\in Y}\sum _{i=1}^{N}p(y=j|\Theta =i,x)\cdot p(\Theta =i|x)\end{array}$$
其中
$$p(\Theta =i|x)=\frac{{\alpha }_i\cdot p(x|{\mu }_i,{\sum }_i)}{{\sum }_{i=1}^N{\alpha }_i\cdot p(x|{\mu }_i,{\sum }_i)}$$
为样本$x$由第$i$个高斯混合成分生成的后验概率，$p(y=j|\Theta =i,x)$为$x$由第$i$个高斯混合成分生成且其类别为$j$的概率。

高斯混合模型参数估计可以用EM算法求解。生成式方法的特点如下：

• 优点：
  • 比较简单
  • 易于实现
  • 在有标记数据极少的情形下往往比其他方法性能更好。
• 缺点：
  • 模型假设必须准确，即假设的生成式模型必须与真实数据分布吻合。否则利用未标记数据反倒会降低泛化性能。但在现实任务中往往很难事先做出准确的模型假设，除非拥有充分可靠的领域知识。

---

3 半监督SVM

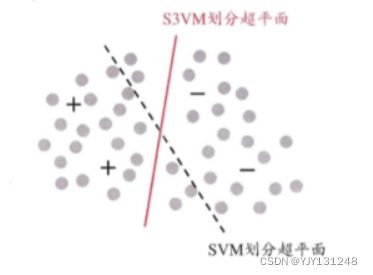
S3VM（半监督支持向量机）：试图找到将两类有标记样本分开，且穿过数据低密度区域的划分超平面。

S3VM算法中最著名的就是TSVM算法（Transductive Support Vector Machine），是一类针对于二分类问题的学习方法。其思想是试图考虑对未标记样本进行各种可能的标记指派（label assignment），即尝试将每个未标记样本分别作为正例或者反例，在所有结果中，寻求一个在所有样本上间隔最大化的划分超平面。

显然上述过程是一个穷举的过程，在实际实现中，必须考虑更高效的优化策略。TSVM采用局部搜索来迭代地找寻最优解。其思路如下：

• 先用有标记样本训练一个SVM，用该模型预测结果作为“伪标记”赋予到未标记样本；
• 求解新的划分超平面和松弛向量；
• 找到两个标记指派为异类且很可能发生错误的未标记样本，交换他们的标记；
• ……

---

4 图半监督学习

对于一个数据集，我们将数据集中每个样本对应于图中的一个结点，结点之间的边的权重相当于样本之间的相关性/相似度。我们可以想象有标记样本的结点颜色染过色，未标记的结点尚未染色。所以半监督学习对应于“颜色”在图上扩散或传播的过程。 且由于图可以对应成一个矩阵，因此，我们可以基于矩阵运算来进行半监督学习算法的推导和分析。

我们基于$D_l$和$D_u$构建一个图$G=(V,E)$，其中结点集$V=\{x_1,x_2,\cdots ,x_l,x_{l+1},\cdots ,x_{l+u}\}$，边集$E$可以表示为一个亲和矩阵，可以根据高斯函数定义为($\sigma$是用户指定的高斯函数带宽函数)
$$(W{)}_{ij}=\{\begin{array}{l}\begin{array}{rl}exp(\frac{-||x_i-x_j|{|}_2^2}{2{\sigma }^2}),& ifi\ne j\\ 0,& othersize\end{array}\end{array}$$
假定从$G=(V,E)$中可以学习到一个实值函数$f:V\to \mathbb{R}$，其对应的分类规则为：$y_i=sign(f(x_i)),y_i\in \{+1,-1\}$。我们可以定义关于$f$的能量函数：
$$\begin{array}{rl}E(f)& =\frac{1}{2}\sum _{i=1}^m\sum _{i=1}^m(W{)}_{ij}(f(x_i)-f(x_j){)}^2\\ & ={\mathbf{f}}^T(\mathbf{D}-\mathbf{W})\mathbf{f}\end{array}$$
其中，$\mathbf{f}=({\mathbf{f}}_l^T{\mathbf{f}}_u^T{)}^T$，$\mathbf{D}=diag(d_1,d_2,\cdots ,d_{l+u})$是一个对角矩阵，$d_i={\sum }_{j=1}^{l+u}(\mathbf{W}{)}_{ij}$为矩阵$\mathbf{W}$第$i$行元素的和。

具有最小能量的函数$f$在据有标记样本上满足$f(x_i)=y_i$，在未标记样本上满足$\Delta f=0$。其中$\mathbf{\Delta }=\mathbf{D}-\mathbf{W}$为拉普拉斯矩阵。

经过一系列计算，我们可以求得$f_u$预测未标记样本：
$$\begin{array}{rl}{\mathbf{f}}_u& =(\mathbf{I}-{\mathbf{P}}_{uu}{)}^{-1}{P}_{ul}{f}_l\\ {\mathbf{f}}_l& =(y_1;y_2;\cdots ;y_l)\end{array}$$
图半监督学习方法在概念上相当清晰，且易于通过对所涉矩阵运算的分析来探索算法性质。但此类算法的缺陷也相当明显：

• 存储开销上：若样本数为$O(m)$，则算法中所涉及的矩阵规模为$O(m^2)$，这使得此类算法很难直接处理大规模数据；
• 构图过程上：难以判知新样本在图中的位置，因此，在接收到新样本时，或是将其加入原数据集对图进行重构并重新进行标记传播，或是需引入额外的预测机制。

---

5 基于分歧的方法

使用分歧的方法使用多学习器，而学习器之间的 “分歧” 对于未标记数据的利用至关重要。这类方法的代表是 “协同训练”。

协同训练基于 “多视图” 视角。例如，对一部电影，图像（画面）是一类属性，声音也是一类属性，每一类属性都能够造出一个属性集，以上面两个属性为例，我们可以构造多视图数据$(<x^1,x^2>,y)$，其中$x^1$是图像数据，$x^2$是声音数据，$y$是标签集，即“爱情片”、“动作片”、“文艺片”等等。

多视图学习基于一个重要假设：不同试图具有相容性，即其所包含的关于输出空间$Y$的信息是一致的。在此假设下，显式地考虑多视图有很多好处：

• 仍以电影为例，某个片段上有两人对视，仅凭图像画面信息难以分辨其类型，但此时若从声音信息听到“我爱你”则可判断出该片段很可能属于“爱情片”；
• 另一方面，若仅凭图像画面信息认为可能是”动作片“，仅凭声音信息也认为可能是“动作片”，则当两者一起考虑时就有很大的把握判别为“动作片”；

显然，在“相容性”基础上，不同视图信息的“互补性”会给学习器的构建带来很多便利。

协同训练利用了多视图的 “相容互补性”。设数据拥有两个充分(sufficient)且条件独立的视图。”充分“是指每个视图都包含足以产生最 学习器的信息；“条件独立”则是指在给定类别标记条件下两个视图独立。在此情形下，可用一个简单的办法来利用未标记数据：

• 首先在每个视图上基于有标记样本分别训练出一个分类器；
• 然后让每个分类器分别去挑选自己“最有把握的”未标记样本赋予伪标记；
• 将伪标记样本提供给另一个分类器作为新增的有标记样本用于训练更新
• ……

这个 “互相学习，共同进步” 的过程不断迭代进行，直到两个分类器都不再发生变化，或达到预先设定的迭代轮数为止。

---

6 半监督聚类

聚类任务中获得的监督信息大致有两种类型：

• 必连（must-link）：样本必属于同一个簇；勿连（cannot-link）：样本必不属于同一个簇；
  • 代表算法：约束$k$均值算法。
  • 过程：该算法是$k$均值算法的扩展。在聚类过程要确保上述约束的以满足，否则返回error提示。
• 少量的有标记样本。
  • 代表算法：约束种子$k$均值算法。
  • 过程：将带有监督信息（标记label）的样本直接作为“种子”，用他们初始化$k$均值算法的$k$个聚类中心，并且在聚类簇迭代更新过程中不改变种子样本的簇隶属关系。