CVPR2022 | 中科大&华为提出用于非对称图像检索的上下文相似性蒸馏

【写在前面】

非对称图像检索，典型的查询端使用小模型，数据库服务器使用大模型，是资源受限场景的有效解决方案。然而，现有方法要么无法实现特征一致性，要么做出强假设，例如，需要来自大型模型的标记数据集或分类器等，这限制了它们的实际应用。为此，作者提出了一个灵活的上下文相似性蒸馏框架来增强小型查询模型并保持其输出特征与大型图库模型的输出特征兼容，这对于非对称检索至关重要。在本文的方法中，作者学习了具有新的上下文相似性一致性约束的小型模型，没有任何数据标签。在小模型学习过程中，它保留了每个训练图像及其相邻图像与大模型提取的特征之间的上下文相似性。这个简单的约束与同时保留一阶特征向量和二阶排序列表保持一致。大量实验表明，所提出的方法在 Revisited Oxford 和 Paris 数据集上优于最先进的方法。

1. 论文和代码地址

Contextual Similarity Distillation for Asymmetric Image Retrieval

论文地址：https://openaccess.thecvf.com/content/CVPR2022/papers/Wu_Contextual_Similarity_Distillation_for_Asymmetric_Image_Retrieval_CVPR_2022_paper.pdf

代码地址：未开源

2. 动机

大多数现有的图像检索方法使用相同的模型将查询图像和图库图像映射到特征向量，这被称为对称检索。为了达到较高的检索准确率，他们通常只是简单地选择一个大模型进行特征提取，这存在效率低下的问题。在一些计算和内存资源有限的实际场景中，例如移动搜索，在用户侧使用大模型进行特征提取是难以承受的，轻量化模型更可取。一种简单的解决方案是直接使用轻量级模型来提取图库和查询的特征，但是由于轻量级模型的表示能力较差，这通常会降低检索精度。在实践中，图库图像可以在具有足够计算资源的情况下离线处理，而查询在最终用户侧进行特征提取，计算能力有限。在这样的非对称检索设置中，采用大型模型来索引画廊图像并采用轻量级模型进行查询是可行的，这在检索准确性和效率之间进行权衡。

轻量级模型适配是非对称检索的核心问题。具体来说，一个最佳的轻量级模型应该将查询映射到与由大型模型提取的图库嵌入相同的嵌入空间。最近的进展通常将特征兼容性限制引入知识蒸馏的框架中并取得了很大进展。在这些方法中，他们在学习的大模型中重用分类器或使用大模型提取正负样本的特征进行对比学习，如上图（a）和(b)。

为了解决上述问题，作者提出了一个灵活的上下文相似性蒸馏（CSD）框架，将知识从大型图库模型转移到轻量级查询模型，同时保持特征兼容性，如上图（c）所示。在本文的框架中，作者采用新的上下文相似性一致性约束来指导具有大型预训练固定模型的轻量级模型的学习。特别是，对于每个训练图像，作者首先使用大型固定模型提取其特征，并在图库中检索其邻居作为锚点。训练图像与其相邻锚点之间的余弦相似度作为上下文相似度来描述相邻关系。此外，作者使用轻量级模型提取同一训练图像的视觉特征，并在由大型模型提取的相邻锚图像的特征上计算其上下文相似度向量。最后，作者优化了大型和轻量级模型之间的上下文相似性的一致性。值得注意的是，整个框架在知识转移过程中不需要训练数据集的监督。

与以前的方法相比，本文的框架有两个优点。首先，它在训练轻量级模型时考虑了上下文一致性约束，同时优化了一阶特征保持和二阶邻居关系保持。其次，本文的框架在知识转移过程中不需要任何训练数据集的监督。因此，可以使用大量未标记的数据来训练轻量级模型，这有助于本文的方法在各种现实世界场景中的应用。

为了评估本文的方法，作者对 Revisited Oxford 和 Paris 数据集进行了全面的实验，这些数据集进一步混合了 100 万个干扰项。消融研究证明了本文框架的有效性和普遍性。本文的方法大大超过了所有最先进的方法。

3. 方法

3.1. Problem Formulation

设 φ(·) 表示在训练集 T 上训练的特征提取器。 φ(·) 用于将图库 G 中的图像 x 映射为 L2 归一化特征向量${\mathbf{f}}_g=\varphi (x)\in {\mathcal{R}}^d$，将用于图库索引的模型表示为${\varphi }_g(\cdot )$。在测试期间，查询模型${\varphi }_q(\cdot )$将图像 q ∈ Q 映射到 L2 归一化特征向量 ${\mathbf{f}}_q={\varphi }_q(q)\in {\mathcal{R}}^d$。 ${\mathbf{f}}_g$和 ${\mathbf{f}}_q$之间的余弦相似度用于计算图像之间的相似度。以 Q 和 G 为条件的检索系统的性能通过一些指标来衡量，例如平均平均精度 (mAP)，将其表示为$P\left({\varphi }_q(\cdot ),{\varphi }_g(\cdot )\mid \mathcal{Q},\mathcal{G}\right)$。具体来说，它是通过用${\varphi }_q(\cdot )$处理查询集Q 和用${\varphi }_g(\cdot )$ 索引图库G 来计算的。为方便起见，忽略查询和图库集并将其表示为$P\left({\varphi }_q(\cdot ),{\varphi }_g(\cdot )\right)$。

假设 ${\varphi }_q(\cdot )$和${\varphi }_g(\cdot )$ 是不同的模型，并且 ${\varphi }_q(\cdot )$在参数尺度上明显小于${\varphi }_g(\cdot )$。对称检索采用${\varphi }_q(\cdot )$或${\varphi }_g(\cdot )$ 处理查询集和图库集，而非对称检索使用${\varphi }_q(\cdot )$嵌入查询图像和 ${\varphi }_g(\cdot )$ 处理图库。非对称检索的一个关键要求是查询模型和图库模型应该兼容，即查询模型的特征嵌入与图库模型的特征嵌入位于相同或非常相似的流形空间中。一般期望$P\left({\varphi }_q(\cdot ),{\varphi }_g(\cdot )\right)>P\left({\varphi }_q(\cdot ),{\varphi }_q(\cdot )\right)$且 $P\left({\varphi }_q(\cdot ),{\varphi }_g(\cdot )\right)\approx P\left({\varphi }_g(\cdot ),{\varphi }_g(\cdot )\right)$，它允许非对称检索在性能和效率之间取得平衡。

3.2. Contextual Similarity Distillation Framework

在这项工作中，作者探索了一种新的上下文相似性约束来学习用于非对称检索的轻量级查询模型${\varphi }_q(\cdot )$。在 ${\varphi }_q(\cdot )$的学习过程中，它使用画廊模型 ${\varphi }_g(\cdot )$ 提取的特征来保留每个训练图像与其邻居之间的上下文相似性。本文的框架概述如上图所示。

在轻量级查询模型的训练过程中，在训练集${\mathcal{T}}_g$上预训练的图库模型${\varphi }_q(\cdot )$被冻结。使用单独的图库${\mathcal{G}}_t$来挖掘相邻图像，作者首先提取 ${\mathcal{G}}_t$ 中的图像特征 $\mathbf{F}=\left[{\mathbf{f}}_g^1,{\mathbf{f}}_g^2,\cdots ,{\mathbf{f}}_g^N\right]\in {\mathcal{R}}^{d\times N}$：

$${\mathbf{f}}_g^i={\varphi }_g\left(g_i\right)\in {\mathcal{R}}^d,fori=1,2,\cdots ,N,$$

其中 $g_i$ 是图库中的第 i 个图像。然后，对于每个训练样本$x\in {\mathcal{T}}_q$，将其嵌入到画廊模型 ${\varphi }_g(\cdot )$和查询模型 ${\varphi }_q(\cdot )$中以获得 g 和 q：

$$\mathbf{g}={\varphi }_g(x)\in {\mathcal{R}}^d,\mathbf{q}={\varphi }_q(x)\in {\mathcal{R}}^d$$

g被视为查询，通过检索算法从图库中获得top-K图像的排名列表$R=\left[r_1,r_2,\cdots ,r_K\right]$作为锚点，其中$r_i$表示第i个的ID图片。作者假设查询图像不包含在图库中，并将其直接插入到排名列表的前面。因此，排序列表中锚图像的特征描述为${\mathbf{F}}_K=\left[\mathbf{g},{\mathbf{f}}_g^{r_1},\cdots ,{\mathbf{f}}_g^{r_K}\right]\in {\mathcal{R}}^{d\times (K+1)}$。

由于图库模型经过良好训练，检索结果充分反映了图库嵌入空间中 x 的邻域结构。作者进一步用上下文相似性来表示这一结构。具体来说，作者计算查询 g 和排名列表的特征${\mathbf{F}}_K$之间的余弦相似度作为上下文相似度：

$${\mathbf{C}}_g=\left[{\mathbf{g}}^T\mathbf{g},{\mathbf{g}}^T{\mathbf{f}}_g^{r_1},\cdots ,{\mathbf{g}}^T{\mathbf{f}}_g^{r_K}\right]\in {\mathcal{R}}^{K+1}$$

对于查询模型${\varphi }_q(\cdot )$提取的特征q，可以得到对应的上下文相似度：

$${\mathbf{C}}_q=\left[{\mathbf{q}}^T\mathbf{g},{\mathbf{q}}^T{\mathbf{f}}_g^{r_1},\cdots ,{\mathbf{q}}^T{\mathbf{f}}_g^{r_K}\right]\in {\mathcal{R}}^{K+1}$$

之后，作者对上下文相似性 ${\mathbf{C}}_g$ 和${\mathbf{C}}_q$施加一致性约束${\mathcal{L}}_c$以优化 ${\varphi }_q(\cdot )$，使得嵌入 q 与图库嵌入空间中的相邻图像具有相同的相邻上下文。值得注意的是，通过计算图库嵌入空间中 g 和 q 的上下文相似性，可以将图库嵌入空间的邻居结构转移到查询嵌入空间并保持它们相互兼容。

由于作者使用非常深的模型（例如 ResNet101）作为图库模型${\varphi }_g(\cdot )$，如果在线使用它来计算图库图像 ${\mathcal{G}}_t$ 和训练图像 ${\mathcal{T}}_g$的特征嵌入，将需要非常大的计算和存储资源。幸运的是，本文的框架不需要优化画廊模型。因此，作者在训练之前提取图库和训练数据集中所有图像的特征。在训练期间，特征被缓存在内存中。对于每个训练样本，找到它的邻居并加载相应的特征。

3.3. Contextual Similarity Consistency Constraints

对于非对称检索，查询模型 ${\varphi }_q(\cdot )$需要特征兼容和保持邻居结构的能力。为此，通过最小化训练集 ${\mathcal{T}}_g$ 上的上下文相似性一致性约束来学习最优 ${\varphi }_q^{\ast }(\cdot )$。在这项工作中，作者考虑了两种类型的一致性损失，即回归损失和 KL 散度损失，将在下面讨论。

L1 and L2 distances

一个简单的选择是鼓励两个模型对相同的输入示例具有密切的上下文相似性。为了衡量向量之间的接近程度，L1 和 L2 距离度量是最流行的两个，作者将回归损失定义如下

$${\mathcal{L}}_D={\left(\sum _{i=1}^{K+1}{\left|{\mathbf{C}}_q^i-{\mathbf{C}}_g^i\right|}^{\alpha }\right)}^{\frac{1}{\alpha }},\alpha =1,2$$

本质上，等价于以下等式：

$${\mathcal{L}}_D^{\alpha }=\underset{\text{first-order }}{{\left|{\mathbf{q}}^T\mathbf{g}-1\right|}^{\alpha }}+\underset{\text{second-order }}{\sum _{i=1}^K{\left|{\mathbf{q}}^T{\mathbf{f}}_g^{r_i}-{\mathbf{g}}^T{\mathbf{f}}_g^{r_i}\right|}^{\alpha }}$$

优化上述约束与优化一阶特征兼容性和二阶排名列表保留损失是一致的。

KL Divergence

优化上述上下文相似性一致性的另一种替代损失是基于 KL 散度。为此，首先将上下文相似度转换为相邻锚点上的概率分布形式：

$$p_j^i=\frac{\exp \left({\mathbf{C}}_j^i/{\tau }_j\right)}{{\sum }_{l=1}^{K+1}\exp \left({\mathbf{C}}_j^l/{\tau }_j\right)},fori=1,2,\cdots ,K+1$$

其中${\tau }_j$是温度系数，$j\in \{q,g\}$。由于排名列表可能包含远离嵌入特征空间中训练图像的图像，因此温度系数 ${\tau }_g$ 设置为小于 1 以保持${\varphi }_q(\cdot )$主要关注训练图像的近邻结构，而不是远距离点。然后，一致性约束可以定义为同一邻居集上两个概率之间的 KL 散度：

$${\mathcal{L}}_{KL}=D_{KL}\left(p_g\Vert p_q\right)=\sum _{l=1}^{K+1}{p}_g^l\log \frac{p_g^l}{p_q^l}$$

作者还将 KL 散度损失分为一阶和二阶项。令 $D_q={\sum }_{l=1}^{K+1}\exp \left(C_q^l/{\tau }_q\right)$和上式可以改写为：

$$\begin{array}{rl}{\mathcal{L}}_{KL}& =\underset{\text{constant }C}{\sum _{l=1}^{K+1}{p}_g^l\log p_g^l}-\sum _{l=1}^{K+1}{p}_g^l\log p_q^l\\ & =C-\underset{\text{first-order }}{\frac{p_g^1}{{\tau }_q}{\mathbf{q}}^T\mathbf{g}}+\underset{\text{second-order }}{p_g^1\log D_q-\sum _{l=2}^{K+1}{p}_g^l\log p_q^l}\end{array}$$

因此，也达到了同时优化一阶和二阶损失的效果。

4.实验

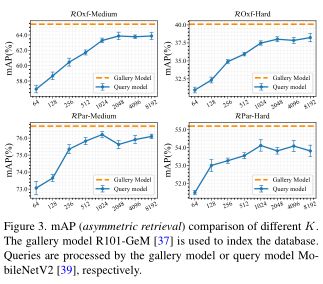
上图显示了本文方法在不同长度的排名列表 R 下的 mAP。随着长度的增加，性能在所有设置下都会增加，但当列表长度 K ≥ 1024 时会饱和。

如上图所示，Random 和 Fixed 选择anchor的变体都会导致性能严重下降，这表明保留近邻的上下文相似性有利于非对称检索。

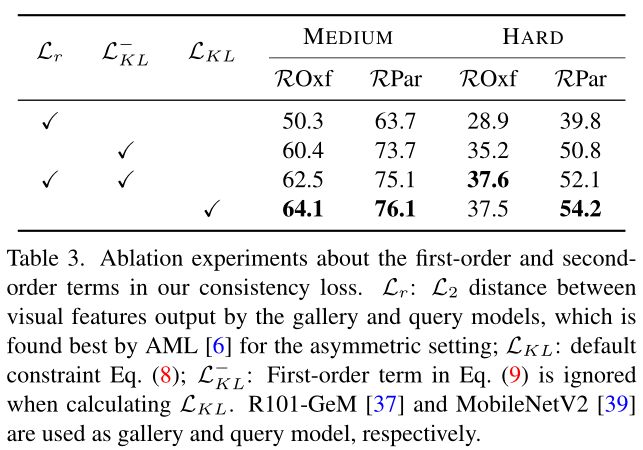
如上表中所示。 L2损失和$L_{KL}$损失都导致良好的性能，而L1损失表现最差。这是因为 L1 损失使用绝对值作为距离，这导致优化困难。作者将 KL 散度作为默认一致性约束。

在上表中，作者进一步验证优化本文的上下文相似性一致性约束与优化一阶特征保留和二阶排名列表保留损失是一致的。

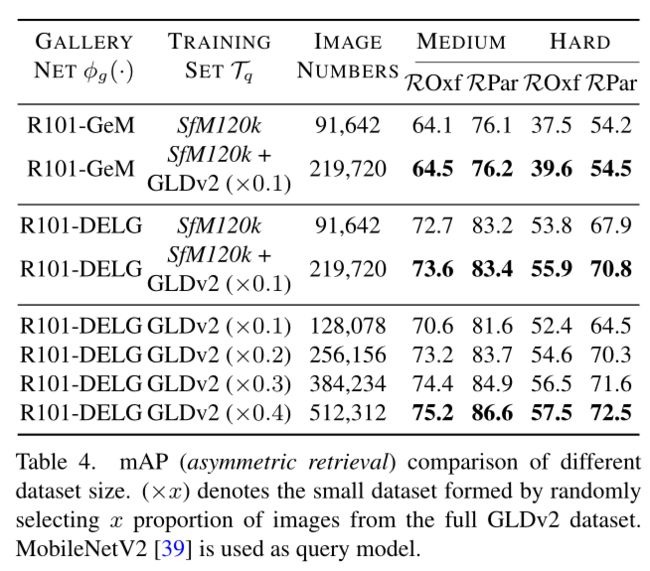
在上表中，作者进一步展示了本文框架的可扩展性。

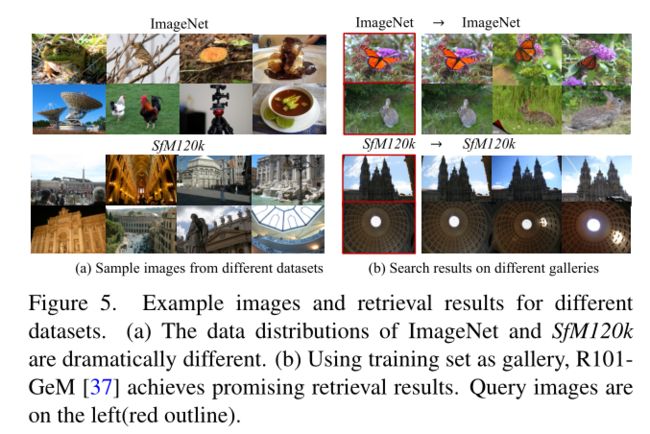
上表展示了数据集上的一些可视化检索结果。

上表表明，当训练数据和图库的分布发生巨大变化时，性能会下降。有趣的是，当采用 ImageNet 作为训练集和图库时，它仍然运行良好。

上图显示了一些 ROxf 和 RPar 图像的嵌入，每个图像都由一个画廊和一个查询模型处理。对于非对称检索，保持特征兼容性至关重要。在训练期间，查询模型被约束以保持每个训练图像与其在图库模型的嵌入空间中的邻居之间的上下文相似性。这使查询和图库模型的输出空间保持兼容。

作者在完整基准上对本文的方法与最先进的方法进行了广泛的比较。如上表中所示，本文的框架在不对称设置下实现了最佳性能。

5. 总结

在本文中，作者提出了一种灵活的上下文相似性蒸馏框架，用于不对称检索。在查询模型训练过程中，采用新的上下文相似性一致性约束来保持每个训练样本与其相邻锚点之间的上下文相似性。优化此约束与优化一阶特征保留和二阶排名列表保留损失是一致的。所提出的框架甚至可以使用来自不同领域的未标记数据集进行训练，这表明了本文方法的普遍性。大量实验证明了本文的方法在不对称检索设置下优于现有的最先进方法。

【技术交流】

已建立深度学习公众号——FightingCV，关注于最新论文解读、基础知识巩固、学术科研交流，欢迎大家关注！！！

推荐加入FightingCV交流群，每日会发送论文解析、算法和代码的干货分享，进行学术交流，加群请添加小助手wx：FightngCV666，备注：地区-学校（公司）-名称

面向小白的顶会论文核心代码库：[https://github.com/xmu-xiaoma666/External-Attention-pytorch](https://github.com/xmu-xiaoma666/External-Attention-pytorch "https://github.com/xmu-xiaoma66