【论文笔记】Distilling the Knowledge in a Neural Network
摘要
提高机器学习算法性能的一个简单方法是在相同的数据上训练多个不同的模型,然后对它们的预测进行平均。但使用整个模型集合进行预测很麻烦,并且计算成本太高。一个有效的解决方法是将集成中的知识压缩到一个单一模型中,经过验证,在MNIST上取得了很好的结果。
介绍
一些复杂模型在训练时能够取得很好的效果,但是在部署时却难以满足用户对延迟和计算资源有更严格的要求,于是我们可以通过蒸馏的方式来简化模型。一旦复杂模型经过训练,我们就可以将其中的知识转移到更适合部署的小模型。
知识指的是模型中学习到的参数值。简单模型学习复杂模型的参数值,这带来的弊端是我们很难看到模型的形式是如何改变的,只能保留相同的“知识”。
知识的一个更抽象的观点是,它是从输入向量到输出向量的映射。对于学习分类任务的复杂模型而言,正常的训练目标是最大化正确答案的概率。但副作用是,训练模型也为错误答案分配概率,即使这些概率大多非常小,其中一些概率也较大。
例如在手写数字识别任务中,正确答案是1的情况下,模型预测1的概率是0.7,但是7和9的概率也很高,原因是这三个数字字形比较接近,预测7的概率可能是0.2,预测9的概率可能是0.1,而其他数字的概率就几乎为0(例子来源于李宏毅课程 )
模型很重要的一个评价指标是它的泛化能力,即能够很好的推广到新数据。但是尽管如此,在训练时通常只是模型在训练集上达到最佳效果。然而知识蒸馏可以解决这一问题。当复杂模型是不同模型的集合时,它平均了不同模型的输出,能够很好的泛化。利用这样的复杂模型来训练小模型,相比于正常训练的小模型,取得的效果更好。
如何将复杂模型的泛化能力转移到小模型?一个方法是使用由复杂模型产生的类概率作为训练小模型的“软目标” 。对于这个迁移阶段,我们可以使用相同的训练集或单独的迁移集。
当繁琐的模型是不同模型的集合时,我们可以使用它们各自预测分布的平均值作为软目标。软目标在每个训练案例中提供的信息比硬目标多得多,训练案例之间的梯度差异也小得多,因此小模型通常可以在比原始繁琐模型少得多的数据上进行训练,并使用更高的学习率。
前文所讲的例子(手写数字识别)是一种理想情况,实际上,错误答案的预测概率也非常的小,与0差异不大,这就使得软目标与硬目标的差异不大。为了解决这个问题,作者提出了温度的概念。
传统softmax的计算方法如下:
y = e x p ( x i ) ∑ j e x p ( x j ) y=\frac{exp(x_i)}{\sum_jexp(x_j)} y=∑jexp(xj)exp(xi)
引入温度T后的softmax如下:
y = e x p ( x i / T ) ∑ j e x p ( x j / T ) y=\frac{exp(x_i/T)}{\sum_jexp(x_j/T)} y=∑jexp(xj/T)exp(xi/T)
T值越大,输出的预测概率越平滑。预测时温度设为1。
用于训练小模型的迁移集可以完全由未标记数据组成(标签由复杂模型产生),或者使用原始训练集。使用原始训练集效果更好,可以将软目标与硬目标共同加入目标函数。
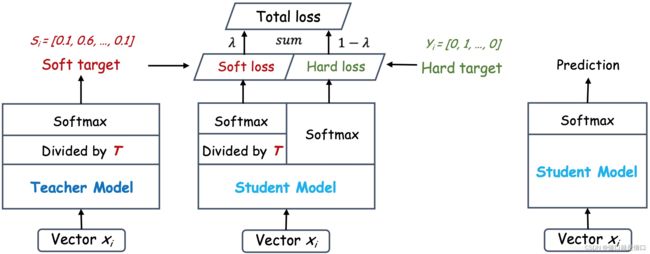
如上图所示,Student Model为小模型,它的模型预测要同时与两个标签进行交叉熵损失计算,一个是由复杂模型(Teacher Model)输出的软目标,一个是原数据集的硬目标(one hot向量),将两者损失加权求和,权重 λ \lambda λ越接近1,对软目标的依赖就越大。
蒸馏
匹配logits(softmax前的输入)是蒸馏的一种特殊情况
梯度计算公式:
∂ C ∂ z i = 1 T ( q i − p i ) = 1 T ( e z i / T ∑ j e z j / T − e v i / T ∑ j e v j / T ) \frac{\partial C}{\partial z_i}=\frac{1}{T}(q_i-p_i)=\frac{1}{T}\Big(\frac{e^{z_i/T}}{\sum_je^{z_j/T}}-\frac{e^{v_i/T}}{\sum_je^{v_j/T}}\Big) ∂zi∂C=T1(qi−pi)=T1(∑jezj/Tezi/T−∑jevj/Tevi/T)
若T远大于logits( z i z_i zi或 v i v_i vi),则 z i / T → 0 , v i / T → 0 z_i/T\to0,v_i/T\to0 zi/T→0,vi/T→0,梯度可近似于:
∂ C ∂ z i ≈ 1 T ( 1 + z i / T N + ∑ j z j / T − 1 + v i / T N + ∑ j v j / T ) \frac{\partial C}{\partial z_i}\approx\frac{1}{T}\Big(\frac{1+z_i/T}{N+\sum_jz_j/T}-\frac{1+v_i/T}{N+\sum_jv_j/T}\Big) ∂zi∂C≈T1(N+∑jzj/T1+zi/T−N+∑jvj/T1+vi/T)
如果假设logits均值为0,即 ∑ j z j = ∑ j v j = 0 \sum_jz_j=\sum_jv_j=0 ∑jzj=∑jvj=0,上式可进一步化简为:
∂ C ∂ z i ≈ 1 N T 2 ( z i − v i ) \frac{\partial C}{\partial z_i}\approx\frac{1}{NT^2}(z_i-v_i) ∂zi∂C≈NT21(zi−vi)
因此,在高温极限下(T无穷大),蒸馏相当于最小化 ( z i − v i ) 2 2 \frac{(z_i− v_i)^2}{2} 2(zi−vi)2(导数为 ( z i − v i ) (z_i-v_i) (zi−vi)),前提是每个迁移集样本的logits均值为0。
以下实验以及结果部分省略
论文地址 Distilling the Knowledge in a Neural Network