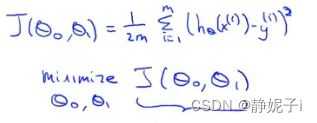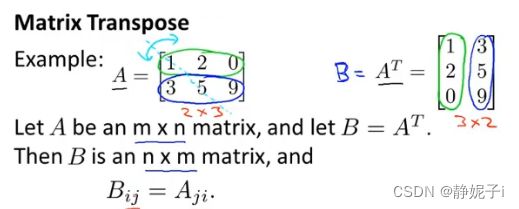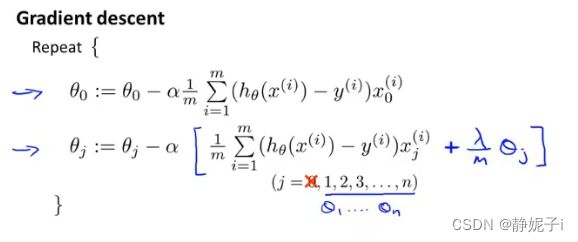机器学习——吴恩达
机器学习——吴恩达
- induction
-
- Supervised learning
- Unsupervised learning
- model
-
- example
- how to work
- define cost function
- gradient descent for minimizing the cost function
- Gradient descent for linear regression
- Matrix and Vector
-
- 定义
- 运算
- multiple feature linear regression
-
- practical tricks for gradient descent
- vectorization
- classification
-
- logistic regression
-
- how to fit parameters theta for logistic regression
- 简化代价函数
- multiclass classification
- overfitting
-
- 什么是过拟合
- 如何解决过拟合问题
-
- regularized linear regression
- regularized logistics regression
- neural network
-
- model
- gradient checking梯度检测
- random initialization
- conclude
induction
what is machine learning？
Task T ; Experience E ; Performance P
classes contain:
Supervised learning
“right answer” given
对于数据集中的每个样本，我们需要预测并得出正确答案
两类问题：回归，分类
example
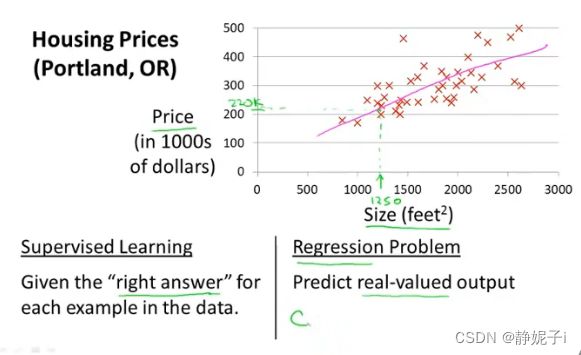
房价预测问题
监督学习：给定实际size与price（right answer）
回归问题：预测连续值
分类问题：预测离散值输出
Unsupervised learning
聚类问题
model
example
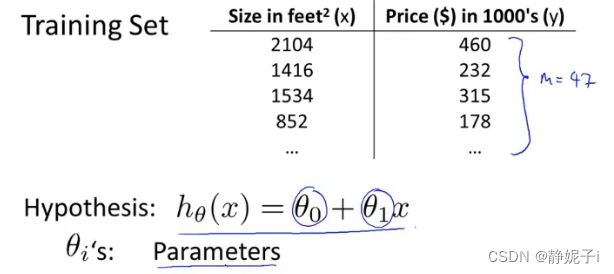
房价预测模型
房价训练集：training set of housing prices
目标：从训练集中学习如何预测房价
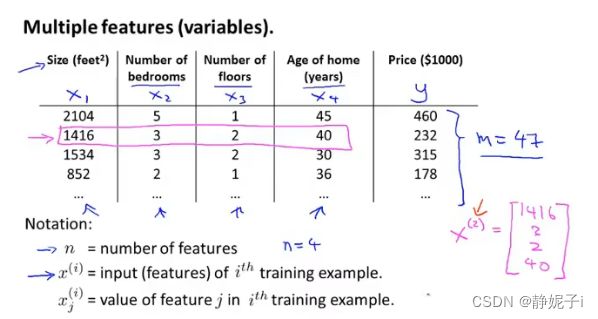
m:训练集大小
x:输入变量/特征
y:输入变量/预测的目标变量
(x,y)：一个训练样本
训练特定样本时使用 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i))表示：第i个训练样本
how to work
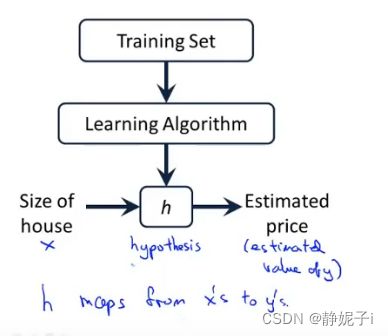
to learing a function: x到y的映射
which called hypothesis
How to represent h?
一种回归问题的假设函数如下
define cost function
linear regression example
模型参数，如何选择？
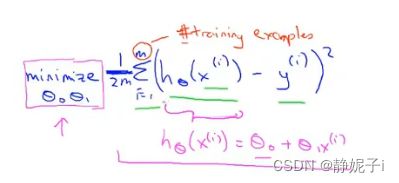
minimize （ h(x)-y ）
最小化训练集中预测值与真实值的差的平方和
cost function——平方误差代价函数（回归中常用）
cost function
固定一个参数，以研究cost function
得到simplified hypothesis function and its cost function
训练集：（1，1），（2，2），（3，3）
θ 1 \theta_{1} θ1分别取1，0.5 , 0…
J ( 1 ) = 0 ; J ( 0.5 ) = 0.68 ; J ( 0 ) = 2.3 J(1)=0 ; J(0.5)=0.68;J(0)=2.3 J(1)=0;J(0.5)=0.68;J(0)=2.3 …
得到 J ( θ ) J(\theta) J(θ)图像：对于每个 θ \theta θ对应着一个不同的假设函数和损失值
线性回归的目标：minimize J ( θ ) J(\theta) J(θ)
保留两个参数的cost function研究
假设函数如下，训练集如下得到所示图像
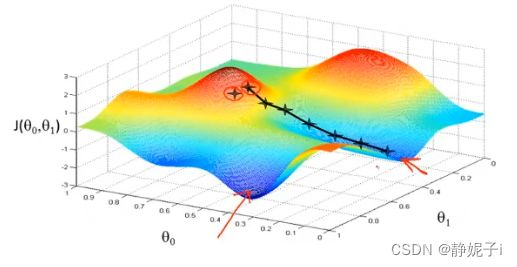
在这里cost function有两个自变量，通过计算可以得到3维空间中图像：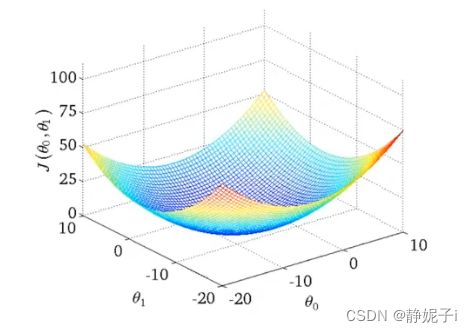
使用等高线图contour plots/figures表示3D图像
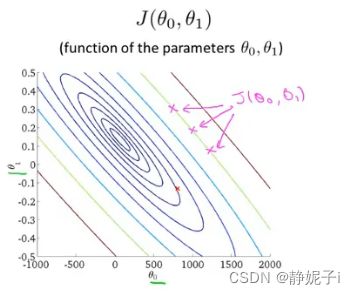
每一圈椭圆上的点的J值相同
靠近最小值的点，拟合效果更好
gradient descent for minimizing the cost function
以两个参数进行举例
for function J ( θ 0 , θ 1 ) J(\theta_{0},\theta_{1}) J(θ0,θ1)——>want m i n θ 0 , θ 1 J ( θ 0 , θ 1 ) \underset{\theta_{0},\theta_{1}}{min} J(\theta_{0},\theta_{1}) θ0,θ1minJ(θ0,θ1)
梯度下降的过程
- start with some θ 0 , θ 1 \theta_{0},\theta_{1} θ0,θ1（通常初始化为0，0）
- keep changing θ 0 , θ 1 \theta_{0},\theta_{1} θ0,θ1 to reduce J ( θ 0 , θ 1 ) J(\theta_{0},\theta_{1}) J(θ0,θ1) until we hopefully end up at a minimum.
gradient descent algorithm
:= 赋值
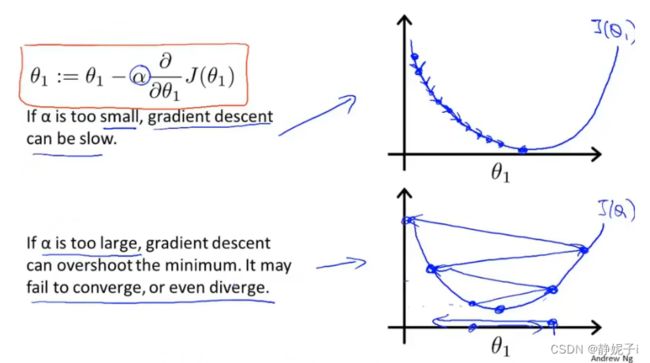
α \alpha α：learning rate控制梯度下降的速度
θ 0 , θ 1 \theta_{0},\theta_{1} θ0,θ1 需要同时更新
α 的影响 \alpha的影响 α的影响
local optima局部最优点
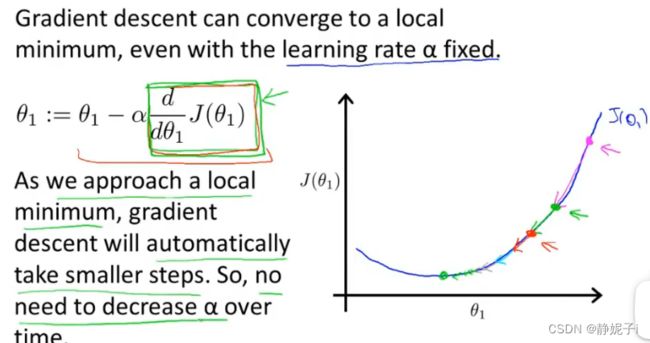
Gradient descent for linear regression
linear hypothesis and squared error cost function
apply gradient descent to minimize squared error cost function
convex function for regression which doesn’t have any local optima（没有局部最优解，只有一个全局最优解）
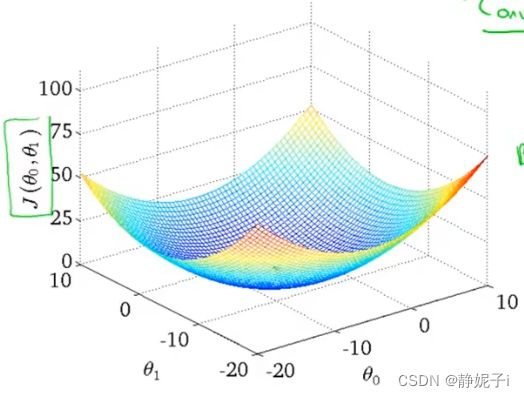
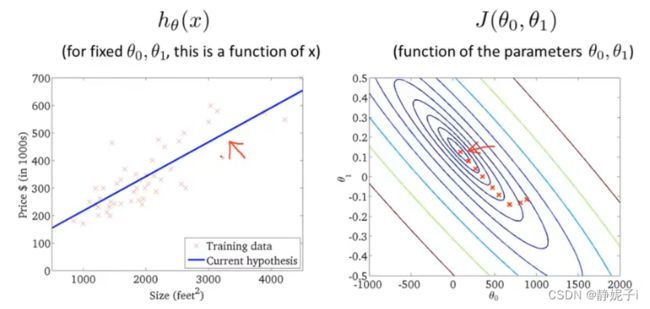batch Gradient descent
Batch：Each step of gradient descent uses all the training examples
Matrix and Vector
定义
matrix
vector
运算
matrix-vector multiplication
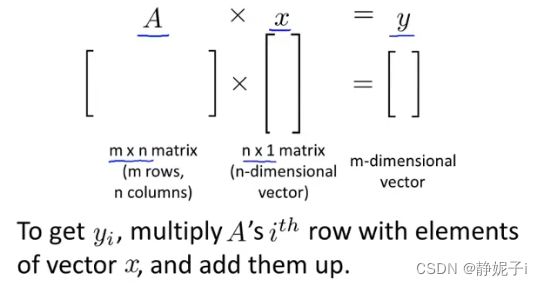matrix-matrix multiplication
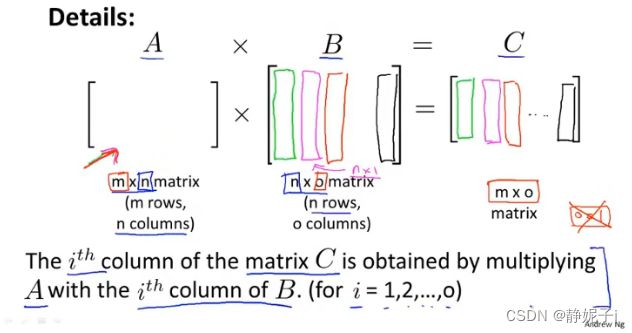
matrix multiplication properties
不满足交换律，满足结合律
inverse and transpose
将没有逆矩阵的矩阵近似看成0
不存在逆矩阵的矩阵术语称为奇异矩阵
multiple feature linear regression
多特征值的回归模型
多元线性回归模型的梯度下降法
practical tricks for gradient descent
feature scaling
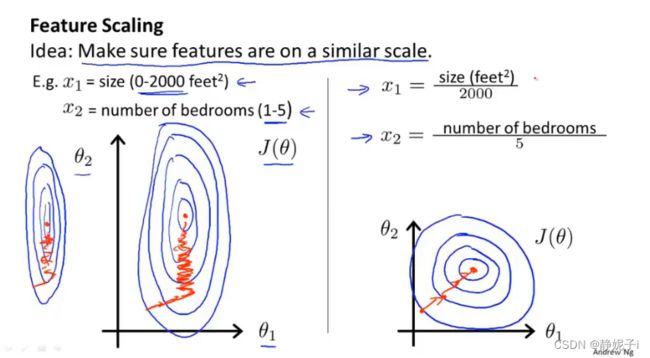特征缩放使之更快的收敛
mean normalization
均值归一化
learning rate
400次迭代后已收敛
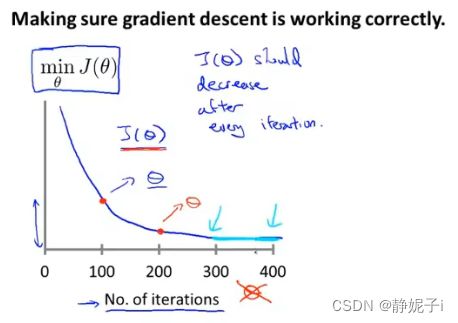
if 损失函数上升 ，说明梯度下降not working
may use a smaller learning rate
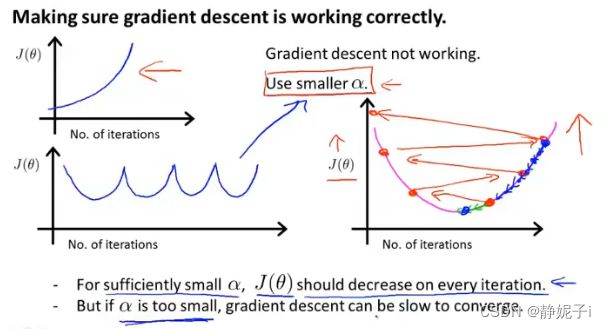
vectorization
classification
logistic regression
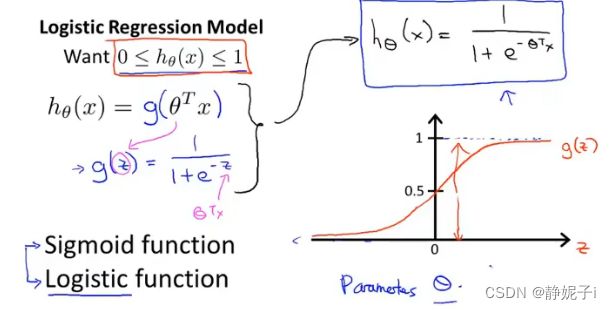
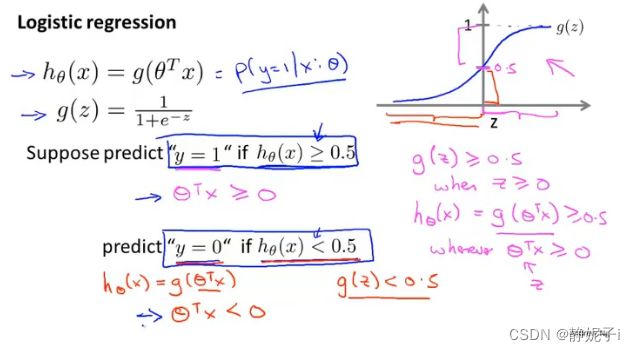decision boundary
是假设函数的一个属性，取决于其参数取值（取决于dataset）
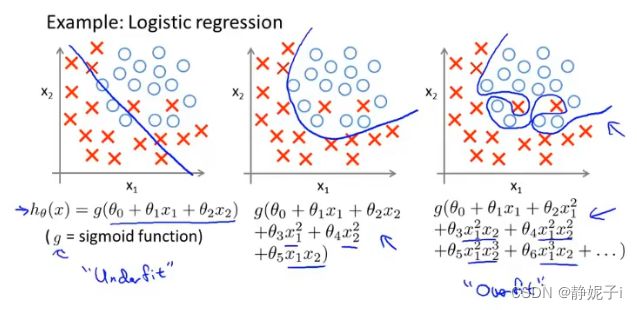
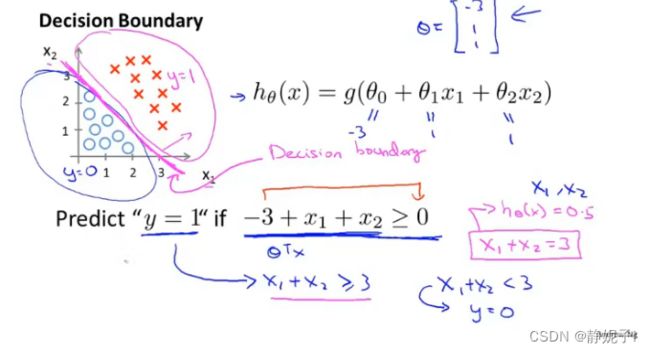non-linear decision boundaries
决策边界不是训练集的属性，而是假设本身及其参数的属性，只要给定了参数向量 θ \theta θ,就能够确定决策边界。
而训练集是为了拟合参数向量 θ \theta θ的
how to fit parameters theta for logistic regression
问题背景
定义损失函数
使用平方误差损失函数，得到会是一个非凸函数（有很多局部最小值，使用梯度下降法难以得到最优解）
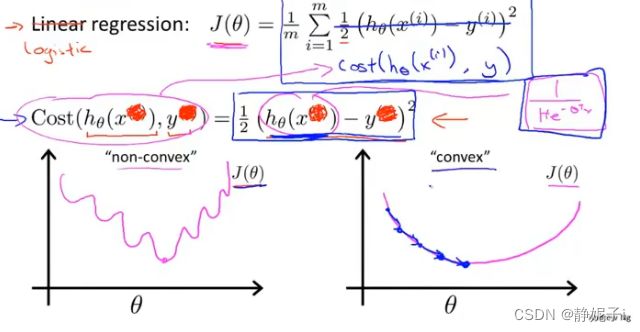logistic regression cost function
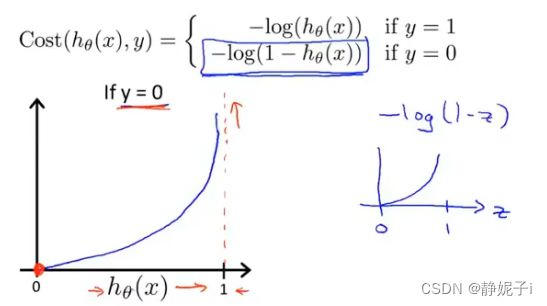
简化代价函数
gradient descent
虽然线性回归和逻辑回归的梯度下降法公式相似，但其假设函数是不同的（h(x)）
multiclass classification
拟合伪二分类器，分别学习各个类别
每个分类器都针对其中一种情况进行训练
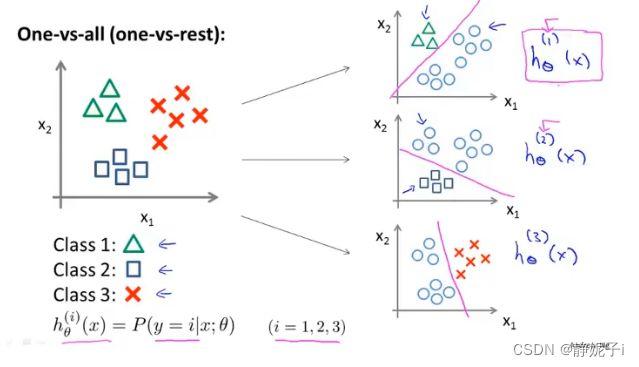
预测：将输入x带入各个分类器并找出h(x)（概率）最大的类别
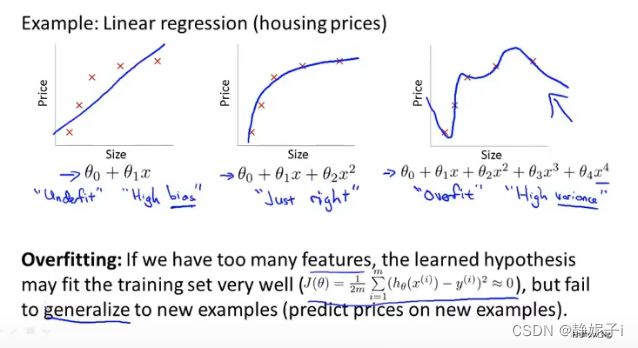
overfitting
什么是过拟合
线性回归中的过拟合
逻辑回归中的过拟合
如何解决过拟合问题
regularized linear regression
在线性回归损失函数的基础上增加正则化项
gradient descent
与未正则化的损失函数相比
每一次更新 θ \theta θ，都要先把 θ \theta θ乘上一个略小于1的数（ 1 − α λ m 1-\alpha \frac{\lambda}{m} 1−αmλ这是正则化后特有的）再进行下降
normal equation(正规方程求解)
regularized logistics regression
gradient descent
neural network
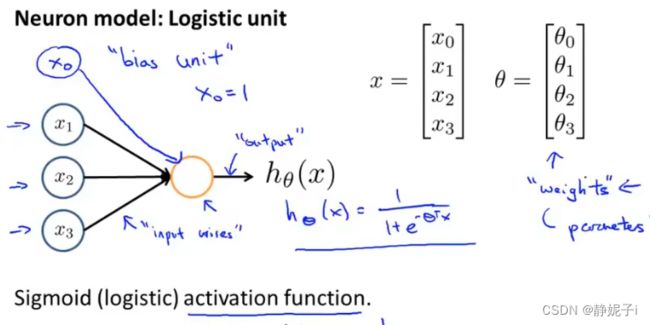
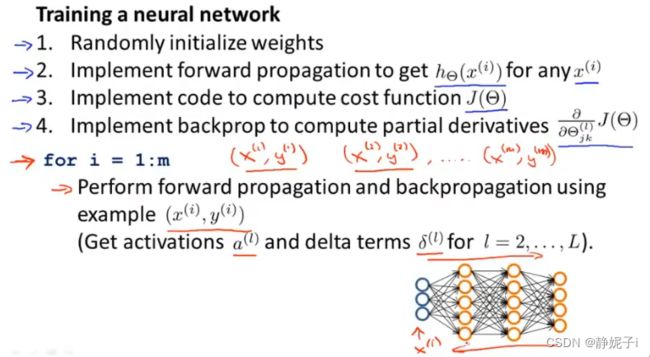
model
使用简单模型模拟单个神经元活动
前向传播的向量化计算
P47
。。。。
gradient checking梯度检测
假设有一个代价函数 J ( θ ) J(\theta) J(θ)图像如下，我们要估计在 θ \theta θ点的梯度
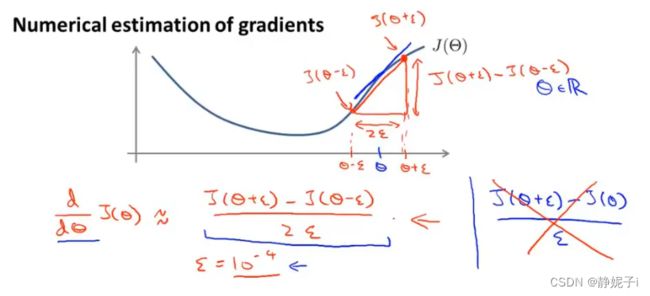
从数值上逼近求解：首先计算出 θ + ϵ \theta+\epsilon θ+ϵ和 θ − ϵ \theta-\epsilon θ−ϵ,并连接两点，则该条直线的斜率即为我们所要求解的导数近似值，可以通过计算 J ( θ + ϵ ) − J ( θ − ϵ ) 2 ϵ \frac{J(\theta+\epsilon)-J(\theta-\epsilon)}{2\epsilon} 2ϵJ(θ+ϵ)−J(θ−ϵ)得到（双侧差分可以得到更准确的结果）
J ( θ + ϵ ) − J ( θ ) ϵ \frac{J(\theta+\epsilon)-J(\theta)}{\epsilon} ϵJ(θ+ϵ)−J(θ)单侧差分
当 θ \theta θ为向量时，估计所有的偏导数
check通过此种方式计算出的梯度与反向传播计算梯度进行对比，是否非常接近，以确定反向传播是否正确
random initialization
对于参数进行初始化——initial Theta
全部设为0，神经网络不工作，所有隐藏单元都在计算相同的特征，得到相同的结果
random initialization
conclude
