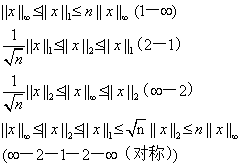数值分析总结笔记1——向量范数、矩阵范数
一.向量范数
1.定义:
对于任意向量x,y以及复数α∈C,函数 f(x)=||x|| 满足以下三个条件:
1.非负性
||x|| ≧ 0, ||x||=0 ⇿ x=0 (n*1)
注意符号,可能会导致不满足非负性
例如:|x1|+|2x2|-5|x3|
注意是否所有x分量为0时,整体也为0
例如:|x1|+|2x2+x3|
2.齐次性
||αx||=|α|·||x||
注意函数中带高次方的情况,是否满足齐次性
3.三角不等式
||x+y|| ≤ ||x||+||y||
称函数||*||为C上的一个向量范数(连续函数)
2.常用向量范数
(写的时候把x1,x2…等等称作元素了,可能不太好。。。)
| 名称 | 等式 | 提示 |
|---|---|---|
| p-范数 | 绝对值-p次方-求和-开方 | |
| 1-范数 | 所有元素的模的和 | |
| 2-范数 | 所有元素模平方和-再开方 | |
| ∞-范数 | 所有元素的模的 最大值 |
3.向量加权范数
对给定的任意向量范数||*||,定义出加权的范数:
![]()
- W:对角矩阵
其对角元素,是其每个分量的权系数
求加权范数时,先将矩阵W乘进去,再带公式
4.向量范数的等价性定理
二.矩阵范数
1.定义
对于任意矩阵A,B以及复数α∈C,函数 f(A)=||A|| 满足以下三个条件:
1.非负性
||A||>=0, ||A||=0 ⇿ A=0
2.齐次性
||αA||=|α|·||A||
3.三角不等式
||A+B|| <= ||A||+||B||
称函数||*||为C(C:m×n)上一个矩阵范数
- 向量范数、矩阵范数定义对比:(由向量转为矩阵,需要注意从n×1到m×n)
(由于编辑器中的 | 会被认作表格边界,所以用 / 代替了 | )
非负性 齐次性 三角不等式 向量范数:f(x)=//x//,x和y为向量 //x//≧0,//x//=0 ⇿ x=0 (n*1) //αx//=/α/·//x// //x+y// ≤//x//+//y// 矩阵范数:f(A)=//A//,A和B为矩阵 //A//≧0, //A//=0 ⇿ A=0 //αA//=/α/·//A// //A+B// ≤//A//+//B//
2.推广得到的常用矩阵范数
为了便于对照和理解,把上面的向量范数和矩阵范数的表放在一起,更好作为对照
其中一些表示需要 矩阵范数相容性 的知识,在后面会写到
| 类别 | 名称 | 等式 | 提示 |
|---|---|---|---|
| 向量范数: | p-范数 | 绝对值-p次方-求和-开方 | |
| 1-范数 | 所有元素的模的和 | ||
| 2-范数 | 所有元素模平方和-再开方 | ||
| ∞-范数 | 所有元素的模的 最大值 | ||
| 矩阵范数: | m1范数 | 所有元素模的和 | |
| F范数 |  |
所有元素模 的平方和-开方 | |
| m∞范数 | 所有元素模 的最大值 |
3.矩阵范数相容性
相比于向量范数,矩阵范数的相容性是向量范数所没有的,原因在于矩阵的乘法
相容性:
对于任意矩阵A∈C(m×l),B∈C(l×n),满足:
![]()
通过证明,矩阵范数的M1范数和F范数都满足相容性,但举例可知M∞范数不具有相容性;
因此,对于M∞范数有特别构造:
![]()
以上构成A的一种相容范数
- 特例:**单位矩阵**的范数
(依然用 / 代替 | )
| 内容 | 结果 |
|---|---|
| //A// m1 | n |
| //A// F | n^(1/2) (即:n的开方) |
| //A// m∞ | n |
4.矩阵范数的等价性定理
依然将矩阵范数和向量范数的等价性定理放在一起进行比较:
(依然用 / 代替 | ,第二行中β,阿尔法为下标)
| 向量范数等价性定理 | 矩阵范数等价性定理 |
|---|---|
| 设//·//β 和//·//α 为C(C:n)上的任意两种向量范数 | 设//·//β 和//·//α 为C(C:m×n)上的任意两种矩阵范数 |
| 存在两个无关正常数c1>0,c2>0 | 存在两个无关正常数c1>0,c2>0 |
| 使得: |
使得: |
| 并称 //·//β 和 //·//α 为C上的等价范数 | 并称 //·//β 和 //·//α 为C上的等价范数 |