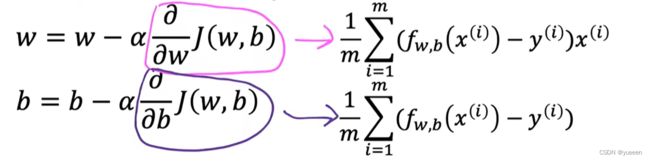week1第一个机器学习模型--线性回归模型
目录
1 机器学习定义
2 主要类型
2.1 监督学习
2.2 无监督学习
3 监督学习模型--回归模型
3.1 线性回归模型
3.2 监督学习过程
3.3 代价函数
3.4 梯度下降
1 机器学习定义
使计算机无需明确编程即可学习的研究领域。 亚瑟 塞缪尔(1959)
2 主要类型
监督学习(使用最多的机器学习类型)、无监督学习、强化学习
2.1 监督学习
1、定义:监督学习是指学习从输入x到输出y的映射的算法。
2、理解:是你给模型学习的数据中包括了正确的答案,即对于给定的输入x,有正确的输出y,模型通过学习正确的(x,y),对于其他没有给定输出结果的输入(它以前从未见过的)给出合理的预测。
3、类型:
回归:从无限多个可能的数字中预测一个数字。
分类:从有限的可能的输出类别中预测一个类别(不一定是数字)。
2.2 无监督学习
1、定义:是指在没有标签的数据中,找到某种结构或模式的算法。
2、理解:是你给模型学习的数据中不带有任何标签(即只给输入x,不给输出y),我们的算法是找到数据中的一些结构、模式,或者只是找到一些有趣的东西,而不是试图监督算法对于每个输入给出正确的答案。
3、类型:
聚类算法:获取没有标签的数据,并尝试将他们自动分到不同的簇中(eg:谷歌新闻分类)
异常检测:检测异常事件。
降维:压缩一个大的数据集,丢失尽可能少的信息。
3 监督学习模型--回归模型
3.1 线性回归模型
1、定义:线性回归意味着将一条直线拟合到你的数据中。是一种特殊的监督学习模型,
![]()
2、举例:房屋价格预测
这是监督学习的一个实例,因为我们是首先给出具有正确答案的数据,然后去预测新房屋的价格。这是回归模型的一个实例,因为它以价格(具有无限种可能的输出)作为预测输出。
还有一种常见的监督学习模型--分类模型::预测类别或离散类别
一些常见的机器学习专业术语
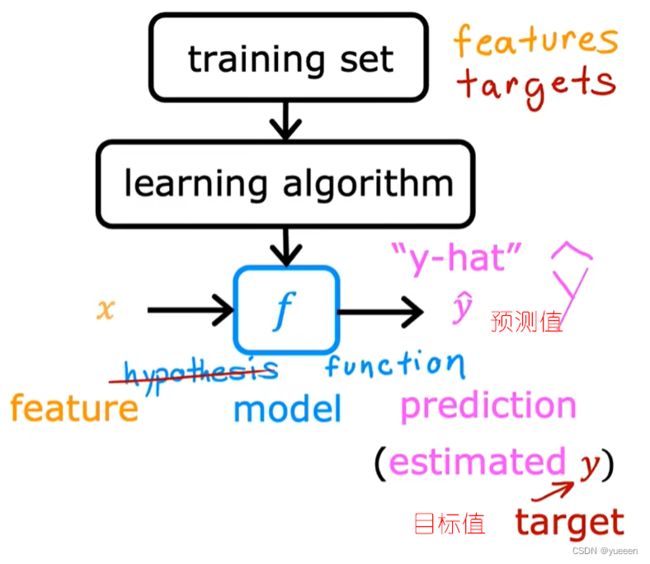
训练集:用于训练模型的数据集
输入变量/ 特征/ 输入特征:给定的作为模型输入的变量,用 x 表示。
输出变量/ 目标变量:作为模型预测输出的变量,用 y 表示。
训练样本总数:用 m 表示。
单个训练样例:用 (x,y) 表示。
第i个训练样例:用 (![]() ,
,![]() ) 表示。
) 表示。
3.2 监督学习过程
而设计学习算法时,关键在于如何表示函数 f ?
这种特殊的模型有个名字:线性回归(一元/单变量线性回归:输入只是单个特征x)
3.3 代价函数
1、为了实现回归算法,第一步就是定义代价函数。它是评价模型的一个指标,有助于去优化模型。
2、对于线性回归模型:![]() ,w 与 b 被称为模型的参数,是你在训练过程中可以调整的变量以改进模型,又被称为系数或权重。
,w 与 b 被称为模型的参数,是你在训练过程中可以调整的变量以改进模型,又被称为系数或权重。
3、我们在视觉上觉得下图这条线适合数据时,意味着这条线大致经过或接近所有训练样例。
对于给定的 x(i),图像上的十字所对应的y轴坐标为 y(i),即真实值;直线上对应的y轴坐标为 y(i)^,即估计值,我们现在要做的事情就是找到 w 和 b ,以便对于所有样例,估计值都能接近真实值,这就是代价函数的作用。
4、均方误差代价函数
即所有样例的估计值减去真实值的平方再求平均。
2是为了后面求导的过程中会把2约掉,使公式看起来更简洁,但无论除不除以2,都不会产生任何影响
5、使用代价函数来找使得Jmin的w和b
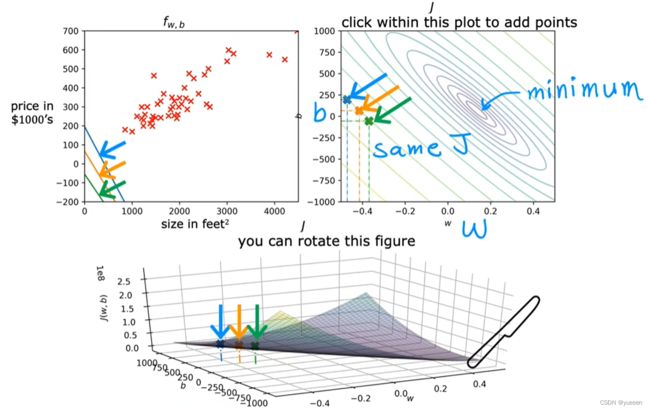
理解:为了简化计算,将参数 b 设为 0。左侧图像是固定参数 w,绘制 x-y 图像,右侧图像是绘制 w-J 图像,因此左侧一条直线对应于右侧一个点。因此如何选择参数 w 的值决定了直线拟合图像拟合的有多好。J 是衡量平方误差有多大的代价函数,所以选择最小化平方误差的 w(此图为w=1时Jmin),会给我们一个很好的模型。因此,线性回归的目标是选择合适的参数以最小化代价函数。
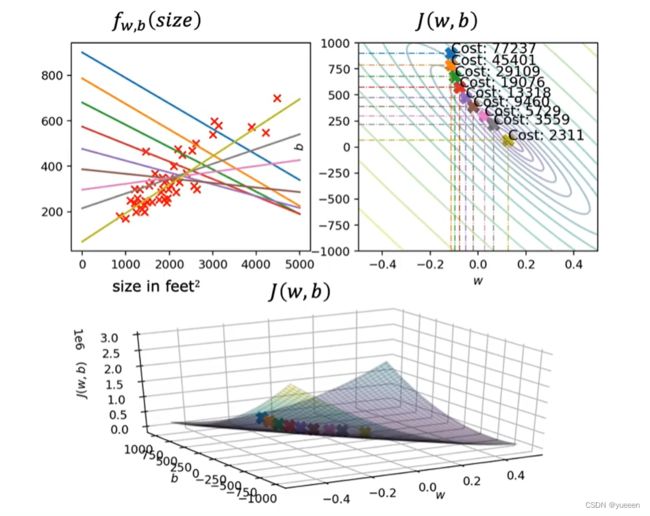
理解:带上w和b。左上是函数 f 的二维图像;右上是函数 J 的等高线图;下面是函数 J 的3D表面图。等高线图上的每个椭圆对应的是3D表面图上处于完全相同高度的点,也就是具有相同的J的点。4要获得等高线图,首先获取3D表面图,然后将其水平切片,每个切片上的所有点对应于一个椭圆。这些同心椭圆的圆心对应代价函数最小的点,直线拟合的越好。
3.4 梯度下降
1、定义:梯度下降所做的事情是:选择参数 w 和 b 的初始值(一般为0);每次更改 w 和 b 的值以减小代价函数的值;直至代价函数达到或接近最小值。
注意:使用梯度下降只能得到局部最小值,对于某些非凸函数(简单理解:不是碗形或吊床形的函数),不能得到全局最小值。比如下图:
站在初始点,自转一周,找到最陡的下降方向,迈出一小步,重复这个过程,直至到达山谷。当改变初始点位置时,重复上述过程, 到达另一山谷。这两个谷底都称为局部极小值
2、梯度下降的公式
① α :学习率,控制下坡迈出多大一步, α 很大,快速的梯度下降过程,反之,一个缓慢的梯度下降过程。常取(0,1) 之间的一个正数
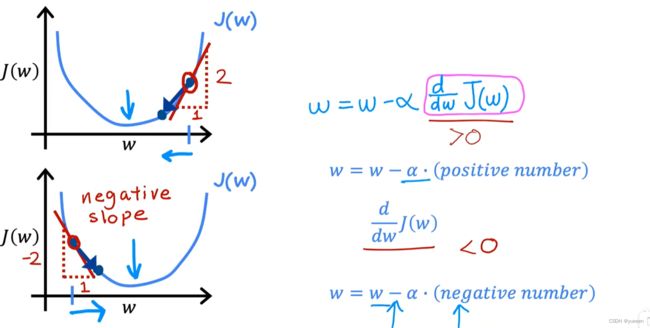
②导数项:代表下坡的方向。一点处的导数值即为该点切线的斜率,切线是朝向右上方时,斜率大于0,朝向右下方时,斜率小于0。当在最小值右侧选值时,更新后的 w 值会减小;当在最小值左侧选值时,更新后的 w 会增大。从而实现走到最低点,如下图:
注意:①重复上述两个公式直至算法收敛(代表达到局部最小值)
②要同时更新 w 和 b,再去赋值。下图左侧是正确的,右侧是错误的
③采用固定的学习率也会达到局部最小值(因为最低点的斜率为0,由梯度下降公式得 w=w,所以并不影响)
3、实现线性回归的梯度下降
均方误差代价函数是凸函数(一个碗形状),只有一个局部最小值即全局最小值,所以只要选择适当的学习率,算法就会收敛。
4、运行梯度下降
随着使用梯度下降法进行参数更新,代价函数逐渐减小,直线也拟合得越来越好。这种梯度下降也被称为批量梯度下降,指的是梯度下降的每一步中我们都使用了所有的训练样本,还有其他种类的梯度下降,每一步更新只使用训练数据的一个子集。