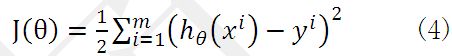机器学习----线性回归

前段时间其实已经写过三篇关于回归类问题的博客，但是那三篇主要注重的是代码练习。本篇博客注重的理论分析。而且对各类回归问题做一个总结，包括一元线性回归，多元线性回归，逻辑回归，岭回归，softmax回归。以前在学习的时候感觉这部分很通畅，没遇到什么大问题，但是昨天复习的时候竟然被几个简单概念给卡主了，最后还是开了吴恩达教授的视频才恍然大悟的，哎正不知道该说什么了。

在正式分析之前，先简单讲几个概念，后面还会详细分析。

1、梯度下降算法。是一种优化算法，优化就是求解一个函数的最大值或最小值。我们在寻找最佳参数时，按照参数梯度的方向去寻找，才能最快的找到最佳解。

2、损失函数。这部分在复习时，把我卡住了。原来在学习的时候很顺畅，但是昨天，有很多细节就是想不通。损失函数就是衡量我们找的参数是不是最佳的函数，那怎么衡量呢？最直观的感觉就是拿预测值和真实值比较，计算一下差异。如果差异越大说明我们找到的参数越差，差异越小说明我们的参数越好。损失函数就是基于这个原理设计的。

正式开讲：

1、线性回归

1.1 一元线性回归

分解：一元：和数学中的概念相同，指的是函数中只有一个变量（一般用x表示）

   线性：是说我们要寻找的预测函数是线性的，也就是直线函数

   回归：就是根据现有数据拟合出一个函数，利用这个函数可以对新数据进行预测，得到预测值。

        

下面我们来举例何为一元线性回归分析，图1为某地区的房屋面积(feet)与价格($)的一个数据集，在该数据集中，只有一个自变量面积(feet)，和一个因变量价格($)，所以我们可以将数据集呈现在二维空间上，如图2所示。利用该数据集，我们的目的是训练一个线性方程，无限逼近所有数据点，然后利用该方程与给定的某一自变量（本例中为面积），可以预测因变量（本例中为房价）。本例中，训练所得的线性方程如图3所示。

                                                  

 图1、房价与面积对应数据集

                                           

                                                          图2、二维空间上的房价与面积对应图

 

                                                                                 图3、线性逼近

同时，分析得到的线性方程为：

        1.2 多元线性回归

       多元线性回归于一元线性回归的区别就在于变量的数量。

  因此，我将两个放在一起分析。

接下来还是该案例，举一个多元线性回归的例子。如果增添了一个自变量：房间数，那么数据集可以如下所示：

                                  

                                                         图4、房价与面积、房间数对应数据集

那么，分析得到的线性方程应如下所示：

因此，无论是一元线性方程还是多元线性方程，可统一写成如下的格式：

上式中x₀=1，而求线性方程则演变成了求方程的参数Θ^T。

线性回归假设特征和结果满足线性关系。其实线性关系的表达能力非常强大，每个特征对结果的影响强弱可以有前面的参数体现，而且每个特征变量可以首先映射到一个函数，然后再参与线性计算，这样就可以表达特征与结果之间的非线性关系。

 从上面的两个例子中我们可以看到，线性回归最终要找的就是h（x）函数，而h（x）函数是由参数θ决定，因此我们最终的目的是找到最佳的θ。这就用到了梯度下降算法。

1.3 梯度下降算法

我们怎样评价我们找到的参数是否最佳呢？这就需要用到损失函数。对线性回归损失函数如下：

前面的系数是为了求导方便而添加的，我们可以看到括号中计算的就是预测值与真实值的差值，之所以对其进行平方操作，因为差值有正有负，进行求和有可能为0，这不是我们想要的。损失函数越小就表示预测值与真实值的差异越小，即我们的h(x)越好。因此最终问题转化成了计算损失函数的最小值问题。

在介绍利用梯度下降求最小值前，先来感受下什么是梯度下降。

     

梯度下降法是按下面的流程进行的：

1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

为了更清楚，给出下面的图：

                                                     

这是一个表示参数θ与误差函数J(θ)的关系图，θ0，θ1表示θ向量的两个维度。J(θ)表示高度。J(θ)的最小值就是图形的谷底所代表的值。那怎么样才能快速的到大谷底呢？我们做个假设，如果你是一个极限运动爱好者，正在玩山地速降，如果你想让速度更快，你一定是找坡度比较陡的坡向下冲。梯度下降算法是一样的，沿着坡陡的地方，才能快速到大谷底。在数学上陡坡就是梯度大的地方。

在上面提到梯度下降法的第一步是给θ给一个初值，假设随机给的初值是在图上的十字点。

然后我们将θ按照梯度下降的方向进行调整，就会使得J(θ)往更低的方向进行变化，如图所示，算法的结束将是在θ下降到无法继续下降为止。

                                                           

当然，可能梯度下降的最终点并非是全局最小点，可能是一个局部最小点，可能是下面的情况：

                                                              

上面这张图就是描述的一个局部最小点，这是我们重新选择了一个初始点得到的，看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点

有了梯度下降算法，下面我们利用梯度下降算法进行参数跟新的推到。

上式中的导数部分就是梯度，theta按照负梯度的方向调整。

最重要的来了，这个梯度怎么求呀！别担心，仔细看下面的推导。

我当时卡主的地方就是对（h（x）- y）求导，我当时把h(x)想成逻辑回归中的sigma函数了，在线性回归中h(x)是线性函数。

有了上面的推导，公式5就演变成了

我们可以看到最后梯度部分就变成了减法和乘法运算。是不是很高兴呢？

1.4 随机梯度下降

       我们再次看看上式中有个求和的操作，如果我们的数据很多几十万个，我们就要疯了，这计算量也忑大了吧。别担心，为了因对这个问题，随机梯度应运而生。

         其实，前面讲的梯度下降算法称之为批量下降，在批量下降算法中损失函数计算的是所有预测值和真实值之间的差异，而在随机梯度中我们只关心当前输入数据的预测值与真实值之间的差异，那这样计算量就小很多。但是，相较于批量梯度下降算法而言，随机梯度下降算法使得J(Θ)趋近于最小值的速度更快，但是有可能造成永远不可能收敛于最小值，有可能一直会在最小值周围震荡，但是实践中，大部分值都能够接近于最小值，效果也都还不错。

修改完损失函数后，参数跟新推导和批量梯度是一样的，这里就不再写了，最终的结果是：

本来想把回归问题总结成一个博客，但是发现已经写了不少了，只能放到下一篇博客了。