SfM和SLAM项目总结

前言：2019年6月27日，我进行了网易伏羲实验室虚拟人方向的电话面试。在电话中，我支支吾吾连自己的项目都讲不清楚。不管最后面试结果如何，自己做过的东西起码自己要懂。

基础知识

内积

$$\mathbf{a}\cdot \mathbf{b}={\mathbf{a}}^{\mathbf{T}}\mathbf{b}=\sum _{\mathbf{i}=1}^3{\mathbf{a}}_{\mathbf{i}}{\mathbf{b}}_{\mathbf{i}}=|\mathbf{a}||\mathbf{b}|\mathbf{c}\mathbf{o}\mathbf{s}<\mathbf{a},\mathbf{b}>$$

外积

$$\mathbf{a}\times \mathbf{b}=\left[\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right]=\left[\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ a_3{b}_1-a_1{b}_3\\ a_1{b}_2-a_2{b}_1\end{array}\right]=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right]\mathbf{b}\triangleq {\mathbf{a}}^{\wedge }\mathbf{b}$$

相应的，有

$$\begin{gathered} \mathbf{a}=[a_1\mathbf{i},a_2\mathbf{j},a_3\mathbf{k}], \\ {\mathbf{a}}^{\wedge }=\mathbf{A}=\left[\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right], \\ {\mathbf{A}}^{\vee }=\mathbf{a} \end{gathered}$$

特殊正交群 $SO(3)$

$$SO(3)=\{R\in {\mathbb{R}}^{3\times 3}|R{R}^T=I,\det (R)=1\}$$

（det为行列式）

特殊欧式群$SE(3)$

$$SE(3)=\{T=\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\in {\mathbb{R}}^{4\times 4}|R\in SO(3),t\in {\mathbb{R}}^3\}$$

李代数$\mathfrak{s}\mathfrak{o}(3)$

在对$R{R}^T=I$进行求导及整理之后，可以得到$R(t{)}^{{}^{\prime }}R(t{)}^T$是一个反对称矩阵，那么就用一个$\varphi (t)\in {\mathbb{R}}^3$与之对应。有：

$$R(t{)}^{{}^{\prime }}R(t{)}^T=\varphi (t{)}^{\wedge }$$

之后求解微分方程，可以得到：

$$R(t)=exp({\varphi }^{\wedge }t)$$

实际求解时利用到指数映射和对数映射。

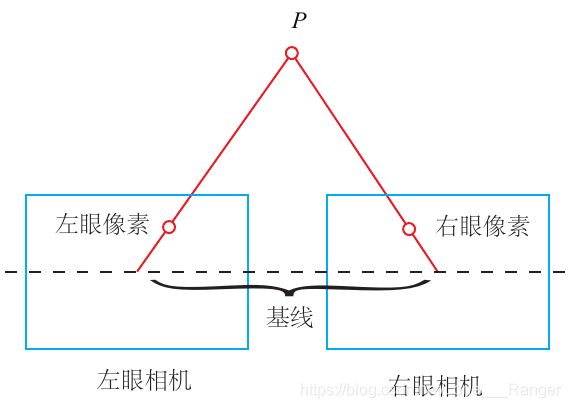
双目系统

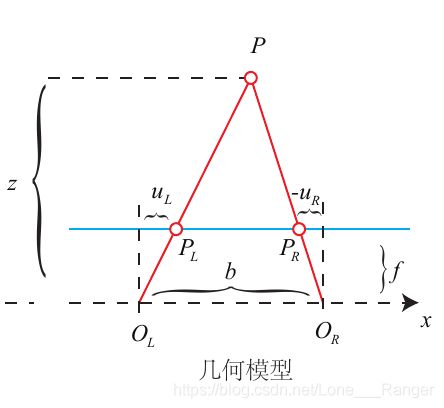
左右相机只有在 x 轴上有位移，因此 P 的像也只在 x 轴（对应图像的 u 轴）上有差异。

$$\frac{z-f}{z}=\frac{b-(u_L+u_R)}{b}$$

整理得:

$$z=\frac{fb}{d},d=u_L-u_R$$

对极几何

[外链图片转存失败(img-OGj4i1u5-1562500349584)(03.jpg)]

两帧图像$I_1,I_2$，两个相机中心分别为 $O_1,O_2$。$p_1,p_2$为互相匹配的特征点。

极平面：连线$O_1{p}_1$和连线$O_2{p}_2$在三维空间中会相交于点 P。这时候点$O_1,O_2,P$三个点可以确定一个平面，该平面称极平面。

极点：$O_1{O}_2$连线与像平面$I_1,I_2$的交点被称为极点。

基线：$O_1,O_2$的连线。

极线：极平面与两个像平面$I_1,I_2$之间的相交线$l_1,l_2$。

用途：双目匹配中，给定左图一个点，能将右图中对应的点的搜索空间缩减到一条线。

条件：需要八个或八个以上的点对

推导：设在第一帧的坐标系下，P坐标为：$\mathbf{P}=[X,Y,Z{]}^T$，两像素点 $p_1,p_2$ **（齐次化坐标）**的像素位置为：

$$s_1{\mathbf{p}}_1=\mathbf{K}\mathbf{P},s_2{\mathbf{p}}_2=\mathbf{K}(\mathbf{R}\mathbf{P}+\mathbf{t})$$

因为是齐次坐标，所以认为等式任意一边乘以非零常数，等式仍然成立。即：

$${\mathbf{p}}_1=\mathbf{K}\mathbf{P},{\mathbf{p}}_2=\mathbf{K}(\mathbf{R}\mathbf{P}+\mathbf{t})$$

取${\mathbf{x}}_1,{\mathbf{x}}_2$是两个像素点的归一化平面上的坐标：

$${\mathbf{x}}_1={\mathbf{K}}^{-1}{\mathbf{p}}_1,{\mathbf{x}}_2={\mathbf{K}}^{-1}{\mathbf{p}}_2$$

有：

$${\mathbf{x}}_2=\mathbf{R}{\mathbf{x}}_1+\mathbf{t}$$

同时左乘$t^{\wedge }$，相当于同时与$t$做外积。

$${\mathbf{t}}^{\wedge }{\mathbf{x}}_2={\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1$$

同时左乘${\mathbf{x}}_2^T$

$${\mathbf{x}}_2^T{\mathbf{t}}^{\wedge }{\mathbf{x}}_2={\mathbf{x}}_2^T{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1$$

因$t^{\wedge }{x}_2$垂直于${\mathbf{x}}_2^T$或$t$，因此左侧为0。***极线约束***即：

$${\mathbf{x}}_2^T{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1=0$$

将${\mathbf{x}}_1={\mathbf{K}}^{-1}{\mathbf{p}}_1,{\mathbf{x}}_2={\mathbf{K}}^{-1}{\mathbf{p}}_2$代回，可得***极线约束***的另一种形式：

$${\mathbf{p}}_2^T{\mathbf{K}}^{-T}{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_1=0$$

意义：

$O_1,P,O_2$三点共面，${\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1$表示极线，且极线一定通过${\mathbf{x}}_2$。

本质矩阵

本质矩阵为：

$$\mathbf{E}={\mathbf{t}}^{\wedge }\mathbf{R}$$

特点：

1. 秩为2
2. 仅依赖于外参
3. 采用摄像机坐标系

基本矩阵

基本矩阵为：

$$\mathbf{F}={\mathbf{K}}^{-T}\mathbf{E}{\mathbf{K}}^{-1}$$

特点：

1. 秩为2
2. 仅依赖于外参和内参
3. 采用像素坐标系
4. F是从左图到右图，有方向，从右图到左图就是F的转置
5. 7个自由度。（$3\times 3$矩阵本有9个自由度，因行列式值为零，相差常数因子，即$kF,k̸=0$,也是基本矩阵，减去两个自由度。）

单应矩阵

单应矩阵是齐次矩阵，有8个未知数，需要四个对应点。

张正友标定法

A Flexible New Technique for Camera Calibration

摘要：张正友标定法只需要相机观察几个（至少两个）不同方向上显示的平面图案。相机或平面图案都可以自由移动。且相机或标定板的运动不需要知道。张正友标定法对径向透镜畸变进行了建模。该方法由一个封闭形式的解组成，然后根据最大似然准则进行非线性改进。

数学推导

针孔相机模型三维点到二维点投影矩阵

符号	含义
$m=[u,v{]}^T$	二维点
$M=[X,Y,Z{]}^T$	三维点
$m=[u,v,1{]}^T$	二维点齐次坐标
$M=[X,Y,Z,1{]}^T$	三维点齐次坐标
s	随机尺度因子
$(\mathbf{R},\mathbf{t})$	外参，即将世界坐标系和相机坐标系联系起来的旋转矩阵和位移向量
$\mathbf{A}$	相机内参矩阵
$\alpha ,\beta$	分别为图像u轴和v轴的尺度因子
$u_0,v_0$	光心的图像坐标系坐标
$\gamma$	描述图像轴u,v之间的倾斜

$$s\mathbf{m}=\mathbf{A}[\mathbf{R}\mathbf{t}]\mathbf{M}$$

其中，

$$A=\left[\begin{array}{ccc}\alpha & \gamma & u_0\\ 0& \beta & v_0\\ 0& 0& 1\end{array}\right]$$

标定板平面与图像之间的单应性矩阵

这里假设标定板所在的平面为空间坐标系下的$Z=0$。

符号	含义
${\mathbf{r}}_{\mathbf{i}}$	旋转矩阵$\mathbf{R}$的第i列

$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\mathbf{A}[\begin{array}{cccc}{\mathbf{r}}_1& {\mathbf{r}}_2& {\mathbf{r}}_3& \mathbf{t}\end{array}]\left[\begin{array}{c}X\\ Y\\ 0\\ 1\end{array}\right]=\mathbf{A}[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& \mathbf{t}\end{array}]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$$

即：

$$s\mathbf{m}=\mathbf{H}\mathbf{M}$$

其中，$\mathbf{H}$为单应矩阵，$\mathbf{H}=\mathbf{A}[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& \mathbf{t}\end{array}]$。

内参约束

假设$\mathbf{H}=\left[\begin{array}{ccc}{\mathbf{h}}_1& {\mathbf{h}}_2& {\mathbf{h}}_3\end{array}\right]$，根据单应关系有：

$$\left[\begin{array}{ccc}{\mathbf{h}}_1& {\mathbf{h}}_2& {\mathbf{h}}_3\end{array}\right]=\lambda \mathbf{A}[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& \mathbf{t}\end{array}]$$

可推出
$${\mathbf{r}}_1=\lambda {\mathbf{A}}^{-1}{\mathbf{h}}_1$$

$${\mathbf{r}}_2=\lambda {\mathbf{A}}^{-1}{\mathbf{h}}_2$$

$${\mathbf{r}}_3={\mathbf{r}}_1\times {\mathbf{r}}_2$$

$$\mathbf{t}=\lambda {\mathbf{A}}^{-1}{\mathbf{h}}_3$$

$$\lambda =\frac{1}{\Vert {\mathbf{A}}^{-1}{\mathbf{h}}_1\Vert }=\frac{1}{\Vert {\mathbf{A}}^{-1}{\mathbf{h}}_2\Vert }$$

根据${\mathbf{r}}_1$和${\mathbf{r}}_2$正交，根据

1. 正交
2. 模相等

有：
$$h_1^T{A}^{-T}{A}^{-1}{h}_2=0$$

$$h_1^T{A}^{-T}{A}^{-1}{h}_1=h_2^T{A}^{-T}{A}^{-1}{h}_2$$

几何解释

需要大于等于三张图像才能确定唯一解。

SfM

三角化

设 $x_1,x_2$ 为两个特征点的归一化坐标，那么它们满足：
$$s_1{\mathbf{x}}_1=s_2\mathbf{R}{\mathbf{x}}_2+\mathbf{t}$$
现在我们已经知道了$\mathbf{R},\mathbf{t}$，想要求解的是两个特征点的深度 $s_1,s_2$。

可以左侧使用$x_1$进行叉乘，使左侧为0，即可求得$s_2$：
$$s_1{\mathbf{x}}_1^{\wedge }{\mathbf{x}}_1=0=s_2{\mathbf{x}}_1^{\wedge }\mathbf{R}{\mathbf{x}}_2+{\mathbf{x}}_1^{\wedge }\mathbf{t}$$
求$s_1$时同理。

PnP

求解 3D 到 2D 点对运动的问题。特征点的 3D 位置可以由三角化，或者由 RGB-D 相机的深度图确定。在单目视觉里程计中，必须先进行初始化，然后才能使用 PnP。

SLAM

ORB_SLAM流程

1. System类生成一个对象slam，初始化slam对象，设置三个线程：Tracking ，LocalMapping ，LoopClosing

2. 订阅 GrabImage() ——> TrackMonocular()——>GrabImageMonocular()——>Track()

三个线程作用

Tracking：

1. Extract ORB，提取关键点和描述子
2. Initialize pose：在Track() 中初始化位姿 pose ， 第一帧 ：mInitialFrame 当前帧：mCurrentFrame ，从这两帧得到 （R，t）。并且，这两帧转为KeyFrame，凡是关键帧KeyFrame都要插入地图 mpMap（mpMap->AddMapPoint(pMP);），根据关键帧与当前帧公共3D点的个数 更新关键帧间的连接关系。

MapPoint类表示 路标点，Map类用Hash表管理 路标点和关键帧。

3. track local map：

   1. 更新局部地图，包括局部关键帧和关键点

   2. 对局部MapPoints进行投影匹配

   3. 根据匹配对估计当前帧的姿态

   4. 根据姿态剔除误匹配

4. keyFrame decision

Local Mapping:

LocalMapping线程处理的关键帧都是Tracking线程发过来的

1. 插入关键帧，
2. 去除冗余的MapPoints；
3. Local BA；
4. 去除冗余的关键帧 : 检测并剔除当前帧相邻的关键帧中和关键帧，剔除的标准是：该关键帧的90%的MapPoints可以被其它关键帧观测到。将当前帧加入到闭环检测队列中。

Loop Closing

1. 回环检测Loop decision：计算闭环候选帧，在候选帧中检测具有连续性的候选帧；
2. 计算相似变换阵sim3，求 [ sR | t ]；
3. Loop Correction：

A. 通过求解的Sim3以及相对姿态关系，调整与当前帧相连的关键帧位姿以及这些关键帧观测到的MapPoints的位置；
B. 将闭环帧以及 与闭环帧相连的关键帧的MapPoints和与当前帧相连的关键帧的点进行匹配；
C. 通过MapPoints的匹配关系更新这些帧之间的连接关系，即更新covisibility graph
D. 对Essential Graph（Pose Graph）进行优化，MapPoints的位置则根据优化后的位姿做相对应的调整
E. 创建线程进行全局Bundle Adjustment

main->构造SLAM对象，在构造函数中设置线程。

读取图像，循环调用trackMonocular，在其中先检查状态是否改变，再调用

GrabImageMonocular

构造了CurrentFrame，最后进行Track