循环神经网络（RNN、LSTM、GRU）以及Pytorch的使用

RNN

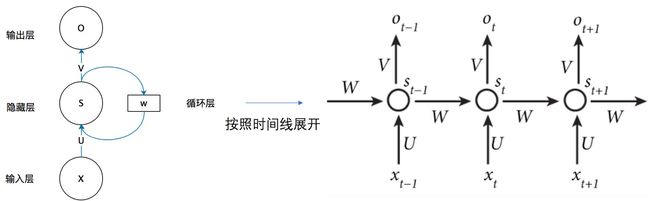
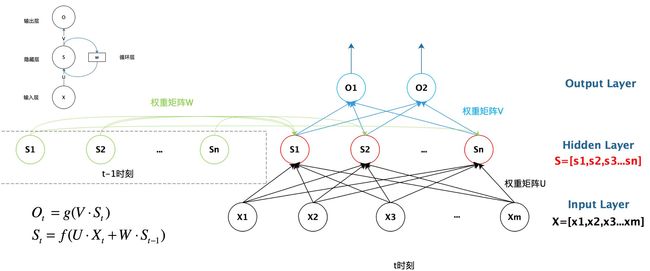
循环神经网络的结构， 它由一个输入层、一个隐藏层和一个输出层组成。

语言模型：给定一个一句话前面的部分，预测接下来最有可能的一个词是什么

在使用RNN之前，语言模型主要采用n-gram, n是一个自然数，假设一个词出现的频率只与前面N个词相关。RNN理论上可以往前（往后看）任意多个词。

参考： 循环神经网络

 在计算时， 每一time step中使用的参数是一样的，也就是说每个步骤的参数都是共享的，这是RNN的重要特点。网络在每个时刻接收到输入之后，隐藏层的值是, 输出层的值是。

， 这里的隐藏变量能够捕捉截至当前时间步的序列的历史信息

裁剪梯度

在循环神经网络中较容易出现梯度衰减或者梯度爆炸。为了应对梯度爆炸，我们可以裁剪梯度(clip gradient)。假设我们把所有模型参数梯度的元素拼接成一个向量，并设置裁剪的阈值是， 裁剪后的梯度 的范数不超过。

GRU(门控循环单元)

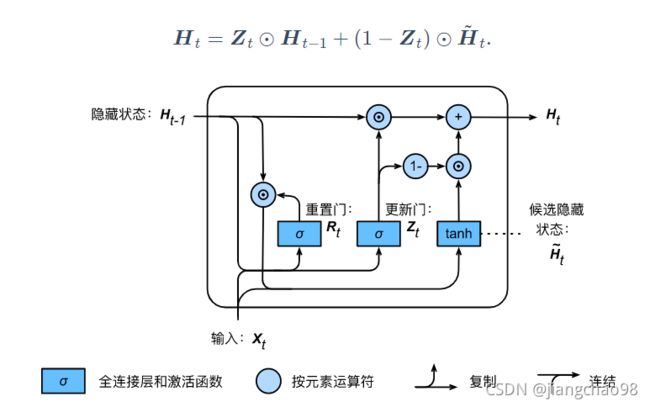
门控循环单元的设计。引入了重置门和更新门的概念，从而修改了循环神经网络中隐藏状态的计算方式。重置门和更新门中每个元素的值域都是[0, 1]

时间步t的候选隐藏状态由重置门和上一时间步的隐藏状态计算得到。重置门控制了上一时间步的隐藏状态如何流入当前时间步的候选隐藏状态。

时间步t的隐藏状态由由当前时间步的更新门和上一步的隐藏状态和当前时间步的候选隐藏状态组合得到。

• 重置门有助于捕捉时间序列里短期的依赖关系；
• 更新门有助于捕捉时间序列里长期的依赖关系。

公式总结：

                        小批量输入，上一时间步隐藏状态：

                        重置门

                        更新门

                        候选隐藏状态

                        隐藏状态

 LSTM（长短期记忆）

 LSTM中引入三个门，输入门（input gate）、遗忘门（forget gate）和输出门（output gate），以及与隐藏状态形状相同的记忆细胞从而记录额外的信息。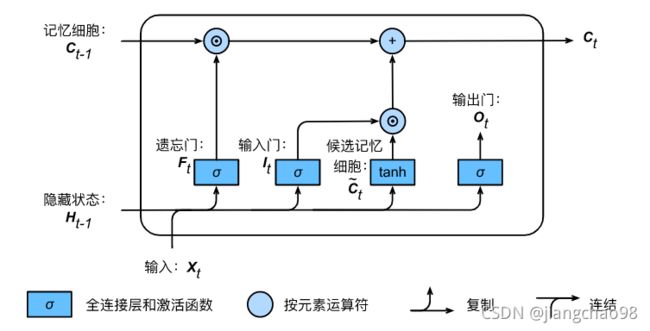

与门控循环单元中的重置门和更新门一样，长短期记忆的门的输入均为当前时间步输入与上一时间步隐藏状态，输出由激活函数为sigmoid函数的全连接层计算得到。三个门元素的值域均为[0, 1]。

输入门、遗忘门、输出门的输出由小批量的输入和上一时间步隐藏状态计算得到。

长短期记忆需要计算候选记忆细胞，使用了值域在[-1, 1]的tanh函数作为激活函数。

通过输入门、遗忘门和输出门来控制隐藏状态中信息的流动，一般是通过使用按元素乘法（符号为）来实现的。当前时间步记忆细胞的计算组合了上一时间步记忆细胞和当前时间步候选记忆细胞的信息，并通过遗忘门和输入门来控制信息的流动：

有了记忆细胞以后，通过输出门来控制记忆细胞到隐藏状态的信息流动：

利用PyTorch实现RNN网络、GRU网络和LSTM网络

通过PyTorch提供的集成好的GRU层、LSTM层进行实现，简单快捷，但缺失一些灵活性。

参考博客 ：读PyTorch源码学习RNN​​​​​​

                   Pytorch中LSTM,GRU参数理解

备注：对于不同的网络层，虽然输入的维度不同，但是通常输入的第一个维度都是batch_size。然而RNN的输入却是（seq_len, batch_size, input_size）,batch_size位于第二维度。此时只需要令参数batch_first = True，即可以将batch_size和序列长度seq_len对换位置。

batch_size为何放在第二维度。因为batch_first意味着模型的输入在内存中存储时，先存储第一个sequence，再存储第二个......。而seq_len first意味着不同序列中同一个时刻对应的输入单元在内存中是毗邻的，这样才能做到真正地batch计算。

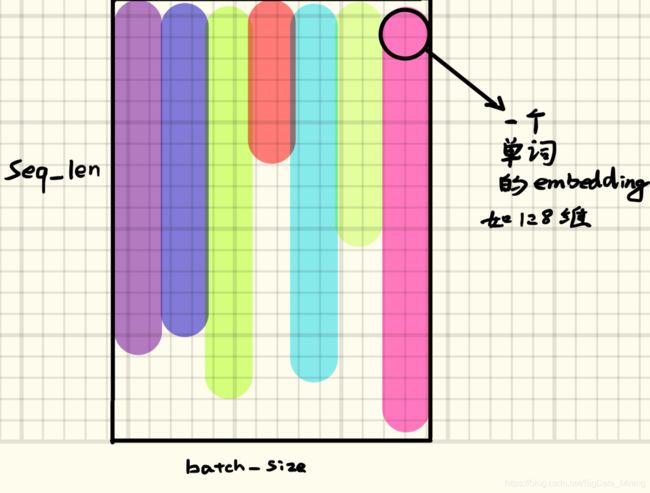
模型输入：三维tensor[seq_len, batch_size, input_dim]
input_dim是输入的维度，一个token的向量维度，eq：128
batch_size是一次往RNN输入句子的数目，eq：8
seq_len是一个句子的最大长度，eq：15

RNN模型的参数
-input_dim 表示输入的特征维度
-hidden_dim 表示输出的特征维度
-num_layers 表示网络的层数
-nonlinearity 表示选用的非线性激活函数，默认是'tanh'
-batch_first 表示输入数据的形式，默认是False，形式（seq_len，batch_size, feature_dim）
-bidirectional 表示是否使用双向的RNN，默认是False

import torch
import torch.nn as nn

#构造RNN网络，x的维度5，隐层的维度10，网络的层数2
rnn_seq = nn.RNN(5, 10, 2)    #将每个token的维度由 5 变成了 10
#构造一个输入序列，句长为6，batch是3，每个单词用长度为5的向量表示
x = torch.randn(6, 3, 5)
out, ht = rnn_seq(x)
print(out.size())   #out的输出维度[seq_len, batch_size, output_dim] [6, 3, 10]
print(ht.size())    #ht的输出维度[num_layers * num_directions, batch_size, hidden_size] [2, 3, 10]


gru_seq = nn.GRU(10, 20, 2) #x_dim, h_dim, layer_num
gru_input = torch.randn(3, 32, 10)
out, h = gru_seq(gru_input)

print(out.size())   #out (3, 32, 20)
print(h.size())     #h  (2, 32, 20)

#LSTM的输出相比于GRU多了一个memory单元
#输入维度50， 隐层维度100， 两层
lstm_seq = nn.LSTM(50, 100, num_layers = 2)
#输入序列seq=10，batch_size = 3, 输入维度 = 50
lstm_input = torch.randn(10, 3, 50)
out, (h, c) = lstm_seq(lstm_input)    #h是隐藏状态、c是记忆细胞

print(out.size())   #(10, 3, 100)
print(h.size())     #(2, 3, 100)
print(c.size())     #(2, 3, 100)

#out[-1] == ht[-1]    在单向的情况下，隐藏单元就是输出的最后一个单元

 在bidirection = True的情况下，每个序列的位置的正向和反向向量维度的拼接

#在双向的情况下， 每个序列位置为正向和反向向量维度的拼接
#输入维度50， 隐层维度100， 两层
lstm_seq = nn.LSTM(50, 100, num_layers = 2, bidirectional = True)
#输入序列seq=10，batch_size = 3, 输入维度 = 50
lstm_input = torch.randn(10, 3, 50)
out, (h, c) = lstm_seq(lstm_input)    #h是隐藏状态、c是记忆细胞

print(out.size())   #(10, 3, 200)
#out.size() 为（10, 3, 200）分别为每个序列位置正向和反向向量维度的拼接
print(h.size())     #(4, 3, 100)    #两层 * 双向 = 4
print(c.size())     #(4, 3, 100)    #两层 * 双向 = 4
#h.size()为（4, 3, 100）分别为每个层次，每个方向的最后一位的隐藏向量（第一层正向、第一层反向、第二层正向、第二层反向......）

#验证模型每个序列位置的输出和隐藏状态之间的关系
out[0][0][-100: -1] = h[-1][0]
#位置0的维度为正向和反向的拼接，反向的值与隐藏状态最后一层反向相等
out[-1][0][:100] = h[-2][0]
#位置-1的维度为正向和反向的拼接，正向的值与隐藏状态最后一层正向相等

验证batch_size = True的情况

模型的输入即为我们平常所使用的形式[batch_size, sequence_length, input_dim] 。对于模型的输出，仍然与模型的输入的顺序相同， 输出维度为[batch_size, sequence_length, hidden_size * num_directions]，对于模型的隐藏状态和记忆细胞，输出维度为[num_layers * num_directions, batch, hidden_size]。

#输入维度50， 隐层维度100， 两层
lstm_seq_ = nn.LSTM(50, 100, num_layers = 2, batch_first = True)

#输入序列seq = 10, batch_size = 3, 输入维度 = 50
lstm_input_ = torch.randn(3, 10, 50) #[batch_size, sequence_length, input_dim]
out_, (h_, o_)= lstm_seq_(lstm_input_)

print(out_.size())    #([3, 10, 100])
print(h_.size())    #([2, 3, 100])
print(o_.size())    #([2, 3, 100])