Pytorch深度学习(四):使用Logistic函数实现二分类以及处理多维度数据输入
Pytorch深度学习(四):使用Logistic函数实现二分类以及处理多维度数据输入
- 参考B站课程:《PyTorch深度学习实践》完结合集
- 传送门:《PyTorch深度学习实践》完结合集
本例中数据集
xdata = torch.Tensor([[1], [2], [3]])
ydata = torch.Tensor([[0], [0], [1]])
0表示不通过,1表示通过,这是一个二分类问题
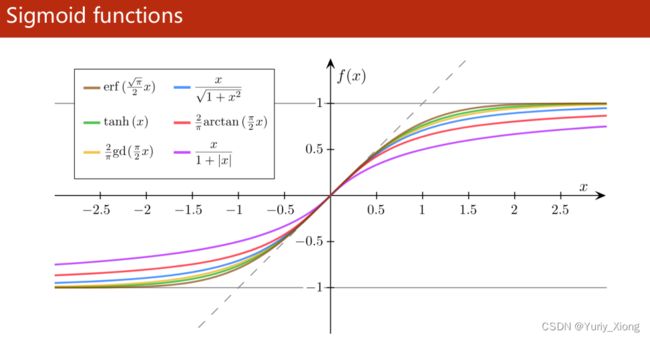
一、Logistic函数
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1
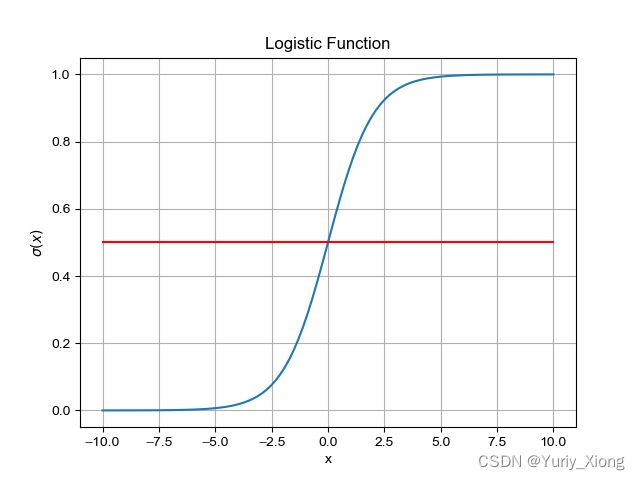
- x → + ∞ , y → 1. x\rightarrow +\infty,\; y\rightarrow 1. x→+∞,y→1.
- x → − ∞ , y → 0. x\rightarrow -\infty,\; y\rightarrow 0. x→−∞,y→0.
- x = 0 , y = 0.5. x=0,\; y=0.5. x=0,y=0.5.
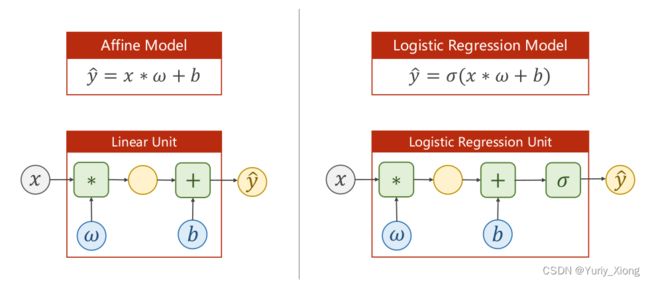
二、分类模型
- 二分类损失函数:
import numpy as np
import matplotlib.pyplot as plt
import torch
# using Logistic Regression solve Binary Classification
xdata = torch.Tensor([[1], [2], [3]])
ydata = torch.Tensor([[0], [0], [1]])
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
ypred = torch.sigmoid(self.linear(x))
return ypred
model = LogisticRegressionModel()
criterion = torch.nn.BCELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
costlist = []
for epoch in range(10000):
ypred = model(xdata)
loss = criterion(ypred, ydata)
# print('epoch=', epoch, loss.item())
costlist.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.plot(range(10000), costlist)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.grid()
plt.title('Error')
plt.subplot(1,2,2)
x = np.linspace(0, 10, 200)
print('xtype:', type(x))
xt = torch.Tensor(x).view((200,1))
yt = model(xt)
y = yt.data.numpy()
plt.plot(x,y)
plt.plot([0, 10], [0.5, 0.5], color='red')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.title('Binary Classification')
plt.show()
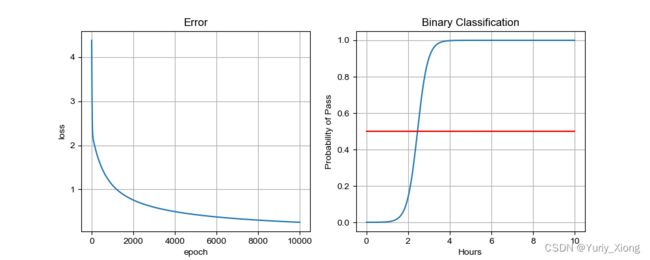
可见,当 x > 4 x>4 x>4后,通过的概率 P ( x ) → 1 P(x)\rightarrow 1 P(x)→1
三、多维度数据的二分类
打开文件diabetes.csv发现这是一个纯数据的文件,我们使用
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype='float32')
来读取文件为一个np.array储存。
若文件带有表头(一般都带有),则我们使用pandas库读取数据df = pd.read_csv('diabetes.csv'),再df.values即为np.array数据
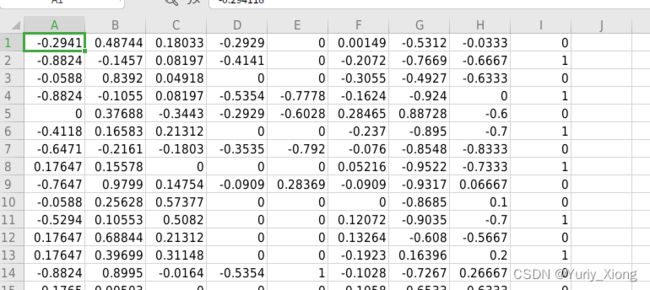
其中,前八列为参数(指标),第九列为结果
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import torch
# 1.Prepare Dataset
# df = pd.read_csv('diabetes.csv')
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype='float32')
print('xy', xy)
xdata = torch.from_numpy(xy[:, :-1])
ydata = torch.from_numpy(xy[:,[-1]]) # s.t.产生数组维数为2,而不是1
# Design model using Class
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
criterion = torch.nn.BCELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
costlist = []
for epoch in range(100):
# Forward
ypred = model(xdata)
loss = criterion(ypred, ydata)
print(epoch, loss.item())
costlist.append(loss.item())
# Backward
optimizer.zero_grad()
loss.backward()
# Upgrade
optimizer.step()
plt.plot(range(100), costlist)
plt.xlabel('epoch')
plt.ylabel('loss')
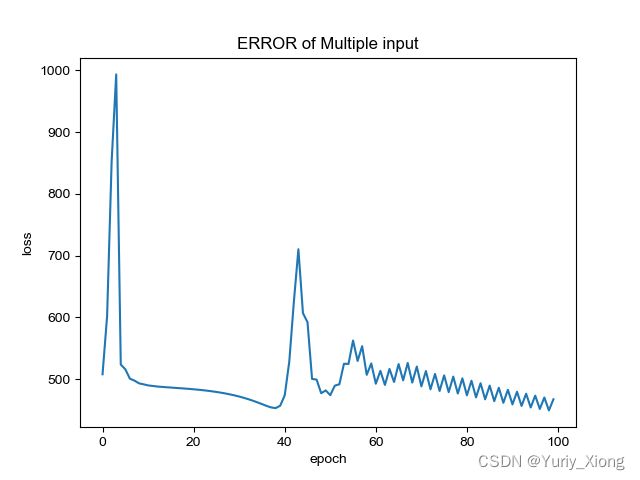
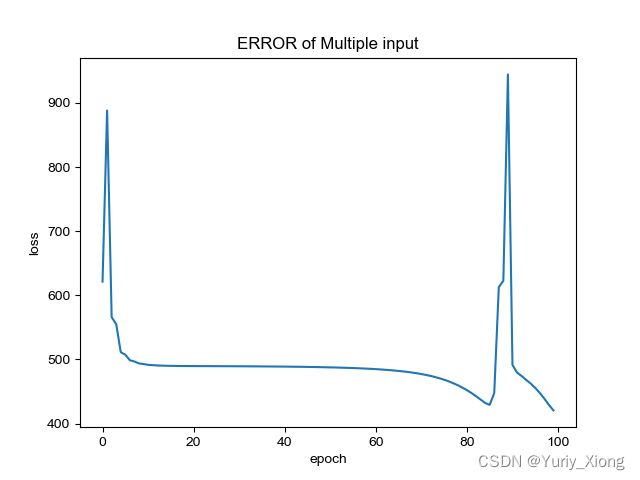
plt.title('ERROR of Multiple input')
plt.show()
发现运行的两次结果都不好且不一致,猜想:
- 优化器不够好
- 迭代次数不够
提高迭代次数
更换优化器为Adam

发现误差的收敛效果更好,且没有震荡出现。由于在程序中我对于BCELoss我们选择了reduction='sum'使得数据看起来较大,实际上,我们可改为reduction='mean'使得数据更小
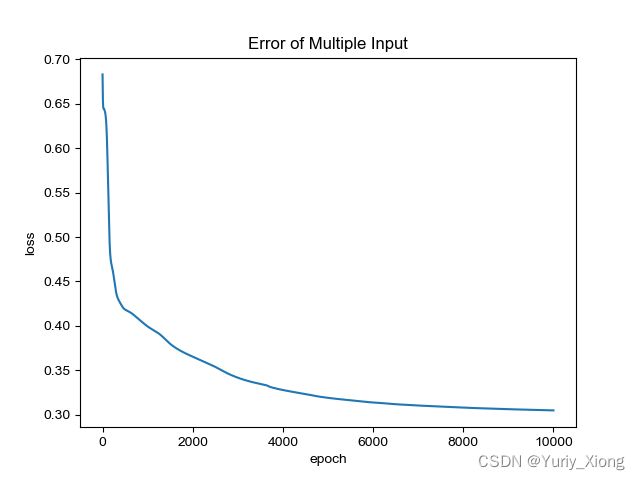
这样loss数据更加美观。
ACC评价指标
但我们发现,loss的值距离0仍然有很大差距,而我们的计算机计算大规模的循环需要等太久,所以我们换一种度量方式以准确率acc为评价指标:如果预测值 y ^ i > 0.5 \hat{y}_i>0.5 y^i>0.5 则取 y ^ i = 1 \hat{y}_i =1 y^i=1,否则取 y ^ i = 0 \hat{y}_i=0 y^i=0
a c c = 1 N ∑ n = 1 N e q ( y ^ , y ) acc = \frac{1}{N} \sum_{n=1}^N eq(\hat{y},y) acc=N1n=1∑Neq(y^,y)
其中 e q eq eq 用于判断 y ^ , y \hat{y},{y} y^,y 是否相等,若相等返回 1,否则返回 0
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import torch
# 1.Prepare Dataset
# df = pd.read_csv('diabetes.csv')
xy = np.loadtxt('diabetes.csv.gz', delimiter=',', dtype='float32')
xdata = torch.from_numpy(xy[:, :-1])
ydata = torch.from_numpy(xy[:,[-1]]) # s.t.产生数组维数为2,而不是1
# Design model using Class
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linear1 = torch.nn.Linear(8, 6)
self.linear2 = torch.nn.Linear(6, 4)
self.linear3 = torch.nn.Linear(4, 1)
self.sigmoid = torch.nn.Sigmoid()
def forward(self, x):
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
return x
model = Model()
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
acclist = []
for epoch in range(10000):
# Forward
ypred = model(xdata)
loss = criterion(ypred, ydata)
# Backward
optimizer.zero_grad()
loss.backward()
# Upgrade
optimizer.step()
# 每1000次学习后,计算一次准确率acc
if epoch % 1000 ==999:
ypredlabel = torch.where(ypred > 0.5, torch.tensor([1]), torch.tensor([0]))
acc = torch.eq(ypredlabel, ydata).sum().item() / ydata.size(0)
print('loss=', loss.item(), 'acc=',acc)
acclist.append(acc)
plt.plot(np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])*1000, acclist)
plt.xlabel('epoch')
plt.ylabel('acc')
plt.title('Accuracy of Classification')
plt.show()
输出的结果为:
loss= 0.3841840624809265 acc= 0.8181818181818182
loss= 0.3535096049308777 acc= 0.8563899868247694
loss= 0.3326750099658966 acc= 0.8708827404479579
loss= 0.32242870330810547 acc= 0.8748353096179183
loss= 0.3158109486103058 acc= 0.8774703557312253
loss= 0.311369389295578 acc= 0.8787878787878788
loss= 0.3073645532131195 acc= 0.8827404479578392
loss= 0.3038375973701477 acc= 0.8814229249011858
loss= 0.30139845609664917 acc= 0.8814229249011858
loss= 0.29956576228141785 acc= 0.8827404479578392
可以见得,我们的准确率是稳固上升的。至此我们就完成多维度数据进行二分类的学习。