高等数学(导数的应用)
目录
- 一.中值定理
-
- 1.1罗尔中值定理
- 1.2 拉格朗日中值定理
- 二.函数的单调性与极值
-
- 2.1 函数的单调性
- 2.2 驻点与极值点
- 2.3 凹凸性
- 2.4 最值
- 2.5 拐点
- 三.导数的应用
一.中值定理
1.1罗尔中值定理
满足:
(1) 在闭区间[a,b]上连续
(2) 在开区间(a,b)内可导 (无尖点)
(3) f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b) (两端同高)
则在开区间(a,b)内至少存在一点 ξ \xi ξ, 使得 f ′ ( ξ ) = 0 f'(\xi)=0 f′(ξ)=0
\quad
例题1: 函数 f ( x ) = cos x f(x)=\cos x f(x)=cosx, 在区间 [ − π 2 , π 2 ] [-\frac{π}{2},\frac{π}{2}] [−2π,2π]内满足罗尔定理的 ξ \xi ξ=______
f ′ ( x ) = − sin x = 0 f'(x)=-\sin x=0 f′(x)=−sinx=0
x=0
\quad
例题2: 下列函数在区间[-1,1]上满足罗尔中值定理所有条件的是____
A. y = 2 x + 1 y=2x+1 y=2x+1 \quad (两边不同高)
B. y = ∣ x ∣ − 1 y=|x|-1 y=∣x∣−1 \quad (有尖点)
C. y = x 2 + 1 y=x^2+1 y=x2+1
D. y = 1 x 2 − 1 y=\frac{1}{x^2}-1 y=x21−1 \quad (有断点, x不能为0)
\quad
例题3: 函数 f ( x ) = ( x − 1 ) 2 f(x)=(x-1)^2 f(x)=(x−1)2满足罗尔条件的区间的是
A. [-1,3] (代点, 相等)
B. [-2,0]
C. [-1,1]
D. [0,3]
\quad
例题4: 若函数 f ( x ) f(x) f(x)在[a,b]上可导, 且 f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b),则 f ′ ( x ) = 0 f'(x)=0 f′(x)=0在(a,b)内_____
A. 至少有一实根
B. 只有一个实根
C. 没有实根
D. 不一定有实根
\quad
例题5: 函数 f ( x ) = x 3 − x f(x)=x\sqrt{3-x} f(x)=x3−x在[0,3]上满足罗尔定理中的数值是_____
f ′ ( x ) = 3 − x + − x 2 3 − x = 0 f'(x)=\sqrt{3-x}+\frac{-x}{2\sqrt{3-x}}=0 f′(x)=3−x+23−x−x=0
解得x=2
\quad
\quad
1.2 拉格朗日中值定理
满足:
(1) 在闭区间[a,b]上连续
(2) 在开区间(a,b)内可导
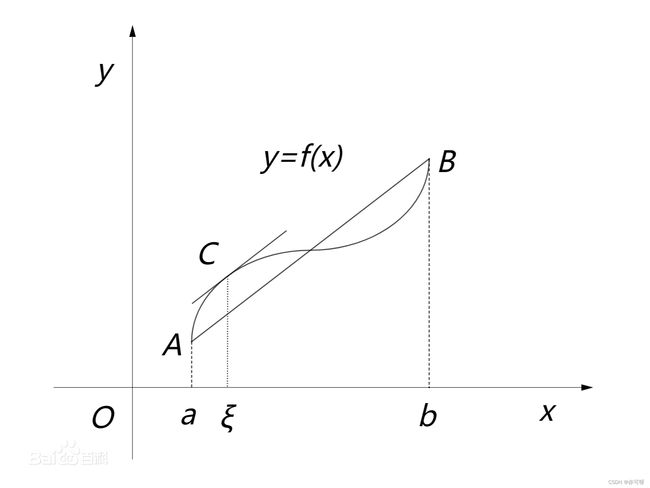
则在开区间(a,b)内至少存在一点 ξ \xi ξ, 使得 f ′ ( ξ ) = f ( b ) − f ( a ) b − a , ξ ∈ ( a , b ) f'(\xi)=\frac{f(b)-f(a)}{b-a}, \quad\xi\in(a,b) f′(ξ)=b−af(b)−f(a),ξ∈(a,b)
其实就是切线公式
\quad
例题6: 函数 f ( x ) = ln ( 1 + x ) f(x)=\ln(1+x) f(x)=ln(1+x)在[0, e-1]上满足拉格朗日中值定理的数值 ξ \xi ξ是____
f ′ ( x ) = 1 1 + x = f ( b ) − f ( a ) b − a = 1 e − 1 f'(x)=\frac{1}{1+x}=\frac{f(b)-f(a)}{b-a}=\frac{1}{e-1} f′(x)=1+x1=b−af(b)−f(a)=e−11
1 + x = e − 1 1+x=e-1 1+x=e−1
x = e − 2 x=e-2 x=e−2
\quad
例题7: 下列区间中, 能使函数 y = 1 x 2 y=\frac{1}{x^2} y=x21满足拉格朗日中值定理全部条件的是
A. [-2,2]
B. [-2,0]
C. [0,2]
D. [-2,-4] (0为断点, 此选项没0)
\quad
例题8: 函数 y = 2 e x y=2e^x y=2ex在区间[0,1]上满足拉格朗日中值定理的 ξ = \xi= ξ=________
f ′ ( ξ ) = f ( b ) − f ( a ) b − a f'(\xi)=\frac{f(b)-f(a)}{b-a} f′(ξ)=b−af(b)−f(a)
y ′ = 2 e x = 2 e − 2 1 − 0 y'=2e^x=\frac{2e-2}{1-0} y′=2ex=1−02e−2
解得 x = ln ( e − 1 ) x=\ln (e-1) x=ln(e−1)
\quad
例题9: 函数 f ( x ) = x − 1 f(x)=\sqrt{x}-1 f(x)=x−1在闭区间内满足拉格朗日中值定理的 ξ = ( 9 4 ) \xi=(\frac{9}{4}) ξ=(49)
\quad
\quad
几次方与图像

\quad
\quad
\quad
二.函数的单调性与极值
\quad
2.1 函数的单调性
设函数 y = f ( x ) y=f(x) y=f(x)在[a,b]上连续, 在(a,b)内可导
(1) 如果在(a,b)内, f ′ ( x ) > 0 f'(x)>0 f′(x)>0, 则函数 y = f ( x ) y=f(x) y=f(x)在(a,b)上单调递增
(2) 如果在(a,b)内, f ′ ( x ) < 0 f'(x)<0 f′(x)<0, 则函数 y = f ( x ) y=f(x) y=f(x)在(a,b)上单调递减
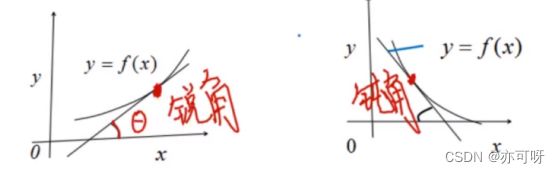
在一个区间内
x 1 x_1 x1< x 2 x_2 x2, f( x 1 x_1 x1)< f( x 2 x_2 x2) 单调递增
x 1 x_1 x1< x 2 x_2 x2, f( x 1 x_1 x1)> f( x 2 x_2 x2) 单调递减
\quad
例题10: 已知 f ′ ( x ) = ( x + 2 ) ( x − 2 ) f'(x)=(x+2)(x-2) f′(x)=(x+2)(x−2), 则函数 f ( x ) f(x) f(x)的单调递减区间是_____
f ′ ( x ) = ( x + 2 ) ( x − 2 ) < 0 f'(x)=(x+2)(x-2)<0 f′(x)=(x+2)(x−2)<0
递减区间是(-2,2)
\quad
2.2 驻点与极值点
满足导数 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0的点 x 0 x_0 x0成为函数 y = f ( x ) y=f(x) y=f(x)的驻点
极值点
可能是
(1) 驻点
(2) 使 f ′ ( x ) f'(x) f′(x)不存在的点 (注:分母为0)
\quad
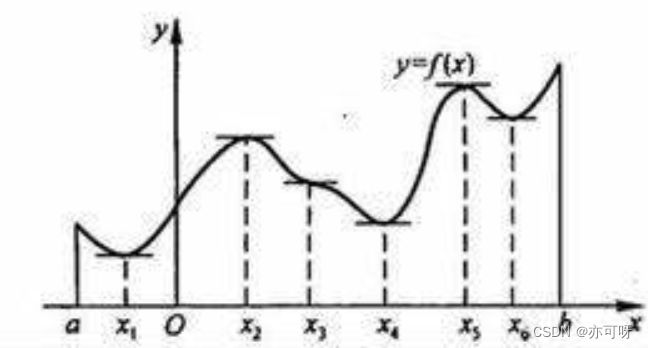
极值的几条定理
(1) 函数的极值未必是最值
(2) 函数的极大值不一定比极小值大
\quad \quad \quad \quad 极小值不一定比极大值大
(3) 函数的极值点一定在区间内部
(4) 函数的最值可能是: (1) 区间内部的极值, (2) 区间的边界值
\quad
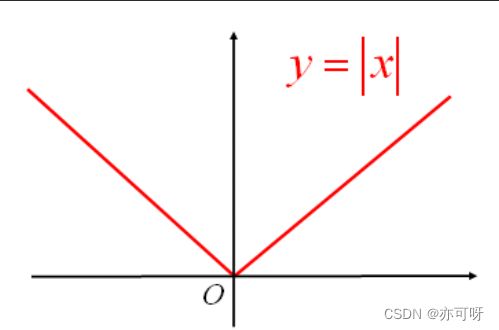
极值点未必是驻点
如 y = ∣ x ∣ y=|x| y=∣x∣在x=0处
\quad
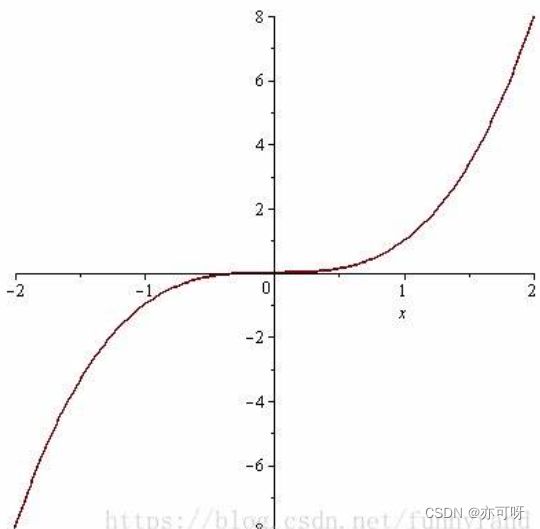
驻点未必是极值点
如 y = x 3 y=x^3 y=x3在x=0处
\quad
\quad
例题11:
已知函数 y = a x 2 + 2 x + c y=ax^2+2x+c y=ax2+2x+c在点 x = 1 x=1 x=1处取得极值2, 则a=____ c=______
a+2+c=2
y ′ = 2 a x + 2 = 0 y'=2ax+2=0 y′=2ax+2=0
解得a=-1, c=1
\quad
\quad
例题12: 函数 y = e x − x − 2 y=e^x-x-2 y=ex−x−2单调递增区间是_______
y ′ = e x − 1 > 0 y'=e^x-1>0 y′=ex−1>0
x>0
增区间是(0,+ ∞ \infty ∞)
\quad
\quad
求极值的步骤
(1) 求出函数的定义域
(2) 求导数 f ′ ( x ) f'(x) f′(x), 求出 f ( x ) f(x) f(x)的驻点和使 f ′ ( x ) f'(x) f′(x)不存在的点
(3) 用这些定义域划分若干区间, 列表
\quad
例题13: 求函数 f ( x ) = x 3 − 3 x 2 − 9 x f(x)=x^3-3x^2-9x f(x)=x3−3x2−9x的极值
定义域为R
f ′ ( x ) = 3 x 2 − 6 x − 9 f'(x)=3x^2-6x-9 f′(x)=3x2−6x−9
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0
3 x 2 − 6 x − 9 = 0 3x^2-6x-9=0 3x2−6x−9=0
解得 x = − 1 x=-1 x=−1或 x = 3 x=3 x=3
| x | ( − ∞ -\infty −∞,-1) | -1 | (-1,3) | 3 | (3,+ ∞ \infty ∞) |
|---|---|---|---|---|---|
| y ′ y' y′ | + + + | 0 | − - − | 0 | + + + |
| y y y | ↑ | 极大值 | ↓ | 极小值 | ↑ |
\quad
例题14: 求函数 f ( x ) = x − 3 2 x 2 3 f(x)=x-\frac{3}{2}\sqrt[3]{x^2} f(x)=x−233x2的极值和单调区间
定义域为R
f ′ ( x ) = 1 − x − 1 3 f'(x)=1-x^{-\frac{1}{3}} f′(x)=1−x−31
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0, \quad 1 − x − 1 3 = 0 1-x^{-\frac{1}{3}}=0 1−x−31=0, 解得x=1
令 f ′ ( x ) f'(x) f′(x)不存在, 1 − 1 x 3 1-\frac{1}{\sqrt[3]{x}} 1−3x1, 则x=0
| x | ( − ∞ -\infty −∞, 0) | 0 | (0,1) | 1 | (1,+ ∞ \infty ∞) |
|---|---|---|---|---|---|
| y ′ y' y′ | + + + | 不存在 | − - − | 0 | + + + |
| y y y | ↑ | 极大值 | ↓ | 极小值 | ↑ |
函数 f ( x ) = x − 3 2 x 2 3 f(x)=x-\frac{3}{2}\sqrt[3]{x^2} f(x)=x−233x2的极大值为0, 极小值为 − 1 2 -\frac{1}{2} −21
在( − ∞ -\infty −∞, 0)和(1,+ ∞ \infty ∞)上单调递增
在(0,1)上单调递减
\quad
例题15: 若 x > 1 x>1 x>1, 证明 2 x > 3 − 1 x 2\sqrt{x}>3-\frac{1}{x} 2x>3−x1
若证 2 x > 3 − 1 x 2\sqrt{x}>3-\frac{1}{x} 2x>3−x1
即证 f ( x ) = 2 x − 3 + 1 x > 0 f(x)=2\sqrt{x}-3+\frac{1}{x}>0 f(x)=2x−3+x1>0
f ′ ( x ) = 1 x − 1 x 2 > 0 f'(x)=\frac{1}{\sqrt{x}}-\frac{1}{x^2}>0 f′(x)=x1−x21>0
则函数 f ( x ) f(x) f(x)在(1,+ ∞ \infty ∞)上单调递增
∵ \because ∵ x > 1 x>1 x>1
∴ \therefore ∴ f ( x ) > f ( 1 ) = 0 f(x)>f(1)=0 f(x)>f(1)=0
∴ \therefore ∴ f ( x ) > 0 f(x)>0 f(x)>0
∴ \therefore ∴ 2 x > 3 − 1 x 2\sqrt{x}>3-\frac{1}{x} 2x>3−x1
\quad
例题16: 若 x > 0 x>0 x>0, 证明 x > sin x x>\sin x x>sinx
即证: y = x − sin x > 0 y=x-\sin x>0 y=x−sinx>0
y ′ = 1 − cos x ≥ 0 y'=1-\cos x\geq0 y′=1−cosx≥0
∴ \therefore ∴ 函数 y = x − sin x y=x-\sin x y=x−sinx在(0,+ ∞ \infty ∞)上单调递增
∴ \therefore ∴ f ( x ) > f ( 0 ) = 0 f(x)>f(0)=0 f(x)>f(0)=0
∴ \therefore ∴ f ( x ) > 0 f(x)>0 f(x)>0
∴ \therefore ∴ x > sin x x>\sin x x>sinx
\quad
例题17: 当 x > 0 x>0 x>0 时, 证明: ln ( 1 + x ) < x \ln(1+x)
即证: f ( x ) = ln ( 1 + x ) − x < 0 f(x)=\ln(1+x)-x<0 f(x)=ln(1+x)−x<0
f ′ ( x ) = 1 1 + x − 1 < 0 f'(x)=\frac{1}{1+x}-1<0 f′(x)=1+x1−1<0
函数 f ( x ) = ln ( 1 + x ) − x f(x)=\ln(1+x)-x f(x)=ln(1+x)−x在(0,+ ∞ \infty ∞)上单调递减
∴ \therefore ∴ f ( x ) < f ( 0 ) = 0 f(x)
∴ \therefore ∴ f ( x ) < 0 f(x)<0 f(x)<0
∴ \therefore ∴ ln ( 1 + x ) < x \ln(1+x)
\quad
例题18: 设函数 f ( x ) = x ∣ x ∣ f(x)=x|x| f(x)=x∣x∣
(1) 证明 f ( x ) f(x) f(x)在点 x = 0 x=0 x=0 处可导, 并求 f ′ ( 0 ) f'(0) f′(0)的值
(2) 讨论函数 f ( x ) f(x) f(x)的单调性
f ( x ) = x ∣ x ∣ = { − x 2 x < 0 x 2 x ≥ 0 f(x)=x|x|=\begin{cases} -x^2 & x<0 \\ x^2 & x\geq0 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\ \end{cases} f(x)=x∣x∣={−x2x2x<0x≥0
(1)
f ( 0 − ) = lim x → 0 − f ( x ) − f ( x 0 ) x − x 0 = lim x → 0 − − x 2 − 0 x − 0 = 0 f(0^-)=\lim\limits_{x\rightarrow 0^-}\frac{f(x)-f(x_0)}{x-x_0}=\lim\limits_{x\rightarrow 0^-}\frac{-x^2-0}{x-0}=0 f(0−)=x→0−limx−x0f(x)−f(x0)=x→0−limx−0−x2−0=0
f ( 0 + ) = lim x → 0 + f ( x ) − f ( x 0 ) x − x 0 = lim x → 0 + x 2 − 0 x − 0 = 0 f(0^+)=\lim\limits_{x\rightarrow 0^+}\frac{f(x)-f(x_0)}{x-x_0}=\lim\limits_{x\rightarrow 0^+}\frac{x^2-0}{x-0}=0 f(0+)=x→0+limx−x0f(x)−f(x0)=x→0+limx−0x2−0=0
∴ \therefore ∴ f ( x ) f(x) f(x)在点 x = 0 x=0 x=0 处可导, f ′ ( 0 ) = 0 f'(0)=0 f′(0)=0
(2)
当 x < 0 x<0 x<0时, f ′ ( x ) = − 2 x > 0 f'(x)=-2x>0 f′(x)=−2x>0, 函数 f ( x ) f(x) f(x)在(- ∞ \infty ∞,0)上单调递增
当 x ≥ 0 x\geq0 x≥0时, f ′ ( x ) = 2 x > 0 f'(x)=2x>0 f′(x)=2x>0, 函数 f ( x ) f(x) f(x)在(0,- ∞ \infty ∞)上单调递增
∴ \therefore ∴ 函数 f ( x ) f(x) f(x)在R上单调递增
\quad
\quad
2.3 凹凸性


要加上等号 y ′ ′ ≤ 0 , y ′ ′ ≥ 0 y''\leq0, y''\geq0 y′′≤0,y′′≥0
\quad
例题19: 若函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0处取得极大值, 则必有
A. f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
B. f ′ ′ ( x 0 ) < 0 f''(x_0)<0 f′′(x0)<0
C. f ′ ( x 0 ) = 0 且 f ′ ′ ( x 0 ) < 0 f'(x_0)=0且f''(x_0)<0 f′(x0)=0且f′′(x0)<0
D. f ′ ( x 0 ) = 0 或 f ′ ( x 0 ) 不存在 f'(x_0)=0或f'(x_0)不存在 f′(x0)=0或f′(x0)不存在
\quad
例题20:
若函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0处具有二阶导数 f ′ ′ ( x 0 ) < 0 f''(x_0)<0 f′′(x0)<0, 且 f ′ ( x ) = 0 f'(x)=0 f′(x)=0, 则 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0是____
A. 极大值
B. 极小值
C. 最大值
D. 最小值
\quad
例题20: 曲线 y = x 3 − 3 2 x 2 + 1 y=x^3-\frac{3}{2}x^2+1 y=x3−23x2+1的凹区间为_______ [ 1 2 , ∞ ) [\frac{1}{2},\infty) [21,∞)
y ′ = 3 x 2 − 3 x y'=3x^2-3x y′=3x2−3x
y ′ ′ = 6 x − 3 > 0 y''=6x-3>0 y′′=6x−3>0
x > 1 2 x>\frac{1}{2} x>21
\quad
\quad
2.4 最值
\quad
例题21: 求函数 f ( x ) = 2 x 3 − 3 x 2 − 12 x + 9 f(x)=2x^3-3x^2-12x+9 f(x)=2x3−3x2−12x+9在[-2,3]上的最大值和最小值
f ′ ( x ) = 6 x 2 − 6 x − 12 f'(x)=6x^2-6x-12 f′(x)=6x2−6x−12
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0, 即 6 x 2 − 6 x − 12 = 0 6x^2-6x-12=0 6x2−6x−12=0, 解得x=-1或x=2
f ( − 1 ) = 16 , f ( 2 ) = − 11 , f ( − 2 ) = 5 , f ( 3 ) = 0 f(-1)=16, f(2)=-11, f(-2)=5, f(3)=0 f(−1)=16,f(2)=−11,f(−2)=5,f(3)=0
∴ \therefore ∴ 函数最大值为16, 最小值为-11
\quad
例题22: 求函数 y = 2 x − x 2 y=\sqrt{2x-x^2} y=2x−x2在 [ 0 , 2 ] \quad[0,2] [0,2]上的最大值和最小值
y ′ = 1 2 2 x − x 2 ∗ ( 2 − 2 x ) = 1 − x 2 x − x 2 y'=\frac{1}{2\sqrt{2x-x^2}}*(2-2x)=\frac{1-x}{\sqrt{2x-x^2}} y′=22x−x21∗(2−2x)=2x−x21−x
令 y ′ = 0 y'=0 y′=0, 解得x=1
令 y ′ y' y′不存在, 解得x=2, x=0
f ( 0 ) = 0 , f ( 1 ) = 1 , f ( 2 ) = 0 f(0)=0, f(1)=1, f(2)=0 f(0)=0,f(1)=1,f(2)=0
∴ \therefore ∴ 函数最大值为1, 最小值为0
\quad
\quad
2.5 拐点
拐点可能出现在:
(1) y ′ ′ ( x ) = 0 y''(x)=0 y′′(x)=0的点
(2) y ′ ′ ( x ) y''(x) y′′(x)不存在的点
\quad
例题23: 已知曲线 y = x 3 + a x 2 + b y=x^3+ax^2+b y=x3+ax2+b的拐点为(1,-1), 求常数a,b 的值
y ′ = 3 x 2 + 2 a x y'=3x^2+2ax y′=3x2+2ax
y ′ ′ = 6 x + 2 a y''=6x+2a y′′=6x+2a
f ( 1 ) = 1 + a + b = − 1 f(1)=1+a+b=-1 f(1)=1+a+b=−1
f ′ ′ ( 1 ) = 6 + 2 a = 0 f''(1)=6+2a=0 f′′(1)=6+2a=0
解得: a=-3, b=1
\quad
例题24: 求曲线 f ( x ) = x 4 − 2 x 3 + 1 f(x)=x^4-2x^3+1 f(x)=x4−2x3+1的凹凸区间及拐点
y ′ = 4 x 3 − 6 x 2 y'=4x^3-6x^2 y′=4x3−6x2
y ′ ′ = 12 x 2 − 12 x y''=12x^2-12x y′′=12x2−12x
令 y ′ ′ = 0 y''=0 y′′=0, 解得x=0,或x=1
| x | ( − ∞ -\infty −∞, 0) | 0 | (0,1) | 1 | (1,+ ∞ \infty ∞) |
|---|---|---|---|---|---|
| y ′ ′ y'' y′′ | + + + | 0 | − - − | 0 | + + + |
| y y y | 凹 | 拐点(0,1) | 凸 | 拐点(1,0) | 凹 |
∴ \therefore ∴ 曲线在区间 ( − ∞ , 0 ) (-\infty,0) (−∞,0)及 ( 1 , + ∞ ) (1,+\infty) (1,+∞)上是凹的, 在区间 ( 0 , 1 ) (0,1) (0,1)上是凸的, 拐点是(0,1)和(1,0)
\quad
\quad
\quad
三.导数的应用
\quad
例题25: 设函数 f ( x ) = 2 x 3 − 3 k x 2 + 1 , k > 0 f(x)=2x^3-3kx^2+1, \quad k>0 f(x)=2x3−3kx2+1,k>0
(1) 当 k = 1 k=1 k=1时, 求 f ( x ) f(x) f(x)在[0,2]上的最小值
(2) 若方程 f ( x ) = 0 f(x)=0 f(x)=0 有3个实根, 求k的取值范围
(1) f ( x ) = 2 x 3 − 3 x 2 + 1 f(x)=2x^3-3x^2+1 f(x)=2x3−3x2+1
f ′ ( x ) = 6 x 2 − 6 x f'(x)=6x^2-6x f′(x)=6x2−6x
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0, 解得, x=1或x=0
则 f ( 0 ) = 1 , f ( 1 ) = 0 , f ( 2 ) = 5 f(0)=1, f(1)=0, f(2)=5 f(0)=1,f(1)=0,f(2)=5
∴ \therefore ∴ 函数 f ( x ) f(x) f(x)在[0,2]上的最小值为 f ( 1 ) = 0 f(1)=0 f(1)=0
(2) f ′ ( x ) = 6 x 2 − 6 k x f'(x)=6x^2-6kx f′(x)=6x2−6kx
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0, 解得 x=0或x=k
则 f ( k ) = 2 k 3 − 3 k 3 + 1 f(k)=2k^3-3k^3+1 f(k)=2k3−3k3+1, 因为k>0
显然 f ( k ) = 2 k 3 − 3 k 3 + 1 < 0 f(k)=2k^3-3k^3+1<0 f(k)=2k3−3k3+1<0
解得 k ∈ ( 0 , + ∞ ) k \in (0,+\infty) k∈(0,+∞)
\quad
例题26: 已知某产品的收益函数 R ( x ) = − 2 x 3 + 3 x 2 + 14 x R(x)=-2x^3+3x^2+14x R(x)=−2x3+3x2+14x, 成本函数 C ( x ) = 2 x + 1 C(x)=2x+1 C(x)=2x+1, 其中x为该产品的产量, 问产量x为多少时利润L(x)最大? 最大利润是多少?
利润=收益-成本
L ( x ) = − 2 x 3 + 3 x 2 + 14 x − 2 x − 1 x > 0 L(x)=-2x^3+3x^2+14x-2x-1\quad\quad x>0 L(x)=−2x3+3x2+14x−2x−1x>0
L ′ ( x ) = − 6 x 2 + 6 x + 12 L'(x)=-6x^2+6x+12 L′(x)=−6x2+6x+12
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0, 解得x=2或x=-1(舍去)
∴ 产量 x 为 2 时利润 L ( x ) 最大 , 最大利润是 27 \therefore 产量x为2时利润L(x)最大, 最大利润是27 ∴产量x为2时利润L(x)最大,最大利润是27
\quad
例题27: f ( x ) = ( x + 1 ) 2 x f(x)=\frac{(x+1)^2}{x} f(x)=x(x+1)2
讨论曲线 y = f ( x ) y=f(x) y=f(x)的几何性质(定义域, 单调性, 凹凸性)
定义域 ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) (-\infty,0) \cup(0,+\infty) (−∞,0)∪(0,+∞)
f ′ ( x ) = 1 − 1 x 2 f'(x)=1-\frac{1}{x^2} f′(x)=1−x21
令 f ′ ( x ) = 0 f'(x)=0 f′(x)=0, 解得x=-1或x=1
令 f ′ ( x ) 不存在 f'(x)不存在 f′(x)不存在, 解得x=0
f ′ ′ ( x ) = 2 x 3 f''(x)=\frac{2}{x^3} f′′(x)=x32
令 f ′ ′ ( x ) 不存在 f''(x)不存在 f′′(x)不存在, 解得x=0
| x | ( − ∞ -\infty −∞, -1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+ ∞ \infty ∞) |
|---|---|---|---|---|---|---|---|
| y ′ y' y′ | + + + | 0 | − - − | / | − - − | 0 | + + + |
| y ′ y' y′ | − - − | − - − | − - − | / | + + + | + + + | + + + |
| y y y | ↑凸 | 极大值 | ↓凸 | / | ↓凹 | 极小值 | ↑凹 |