混合反向学习算法和非线性收敛因子的鲸鱼优化算法
文章目录
- 一、理论基础
-
- 1、鲸鱼优化算法
- 2、改进的鲸鱼优化算法
-
- (1)混合反向学习算法
- (2)非线性收敛因子
- (3)IWOA算法流程图
- 二、仿真实验与分析
- 三、参考文献
一、理论基础
1、鲸鱼优化算法
请参考这里。
2、改进的鲸鱼优化算法
(1)混合反向学习算法
本文采用混合反向学习算法,在每次迭代鲸鱼种群的位置更新之后,将当前种群个体按适应度排序,取适应度较大的前一半个体,计算其反向种群,将得到的反向种群与原鲸鱼种群进行比较,保留适应度较优个体。并且在计算反向种群时引入反向学习因子,以加强算法的全局探索能力。假设在第 t t t次迭代中,鲸鱼种群为 P ( t ) = { x i , j } , i = 1 , 2 , ⋯ , N ; j = 1 , 2 , ⋯ , D P(t)=\{x_{i,j}\},i=1,2,\cdots,N;j=1,2,\cdots,D P(t)={xi,j},i=1,2,⋯,N;j=1,2,⋯,D(其中 N N N为鲸鱼种群的规模; D D D为可行解的维数),反向种群 P ′ ( t ) = { x i , j ′ } P'(t)=\{x'_{i,j}\} P′(t)={xi,j′}则可以通过以下公式计算出反向种群。 x i , j ′ = l ( x min , j + x max , j − x i , j ) (1) x_{i,j}'=l(x_{\min,j}+x_{\max,j}-x_{i,j})\tag{1} xi,j′=l(xmin,j+xmax,j−xi,j)(1)其中, l l l为反向学习因子,是区间 [ 0 , 2 ] [0,2] [0,2]上的随机数; x max , j x_{\max,j} xmax,j和 x min , j x_{\min,j} xmin,j分别为搜索代理 x i x_i xi的第 j j j维元素的最大值和最小值。然后,计算当前种群个体适应度 f i t n e s s ( i ) fitness(i) fitness(i)与反向种群个体适应度 f i t n e s s ′ ( i ) fitness'(i) fitness′(i),若反向种群个体适应度优于当前种群个体,则用反向种群个体代替当前种群个体。
(2)非线性收敛因子
本文提出一种分段的非线性收敛因子,具体公式如下: a = { 2 cos ( t T π ) , t ≤ T 2 2 cos ( t T π ) + 2 , t > T 2 (2) a=\begin{dcases}2\cos(\frac tT\pi),\quad\quad\,\,\,\, t\leq\frac T2\\\\2\cos(\frac tT\pi)+2,\quad t>\frac T2\end{dcases}\tag{2} a=⎩⎪⎪⎪⎨⎪⎪⎪⎧2cos(Ttπ),t≤2T2cos(Ttπ)+2,t>2T(2)在整个迭代过程中,非线性收敛因子分别在前半段和后半段从2减小到0,并且前半段下降的速度逐渐增大,后半段下降的速度逐渐减小,使得改进后的鲸鱼群算法可以更好地适应复杂的搜索过程。
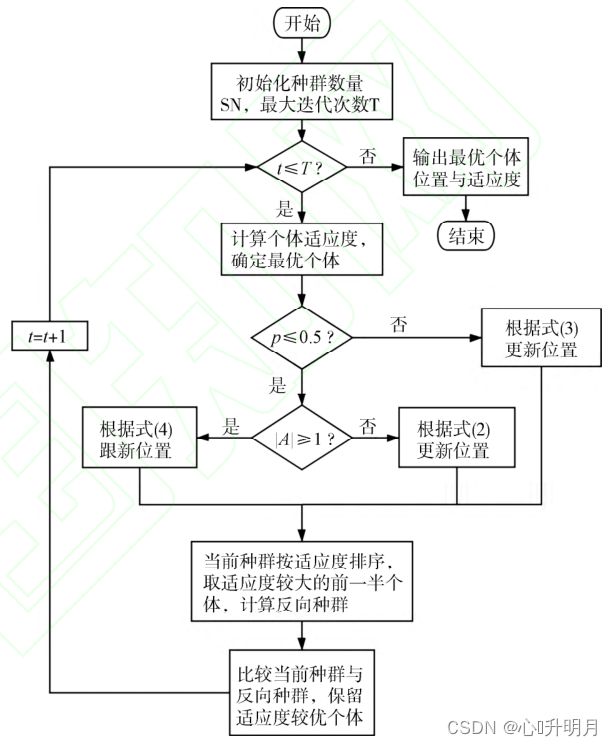
(3)IWOA算法流程图
二、仿真实验与分析
将本文提出的IWOA算法与WOA算法、灰狼优化算法(GWO)、引力搜索算法(GSA)、粒子群算法(PSO)进行对比,为使测试结果更加客观,所有算法的种群规模设置为30、最大迭代次数设置为500,每个算法独立运行30次,以文献[1]中表1为例,结果显示如下:
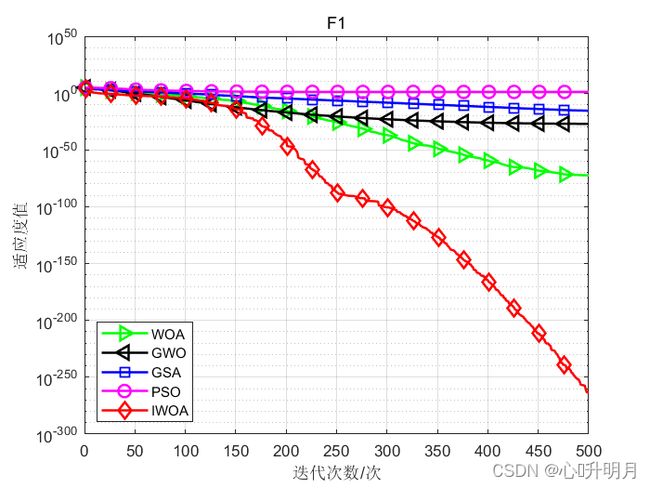



函数:F1
WOA:最差值: 9.5356e-72, 最优值: 7.7392e-85, 平均值: 4.0225e-73, 标准差: 1.7585e-72, 秩和检验: 3.0199e-11
GWO:最差值: 5.3117e-27, 最优值: 4.9724e-29, 平均值: 9.1418e-28, 标准差: 1.175e-27, 秩和检验: 3.0199e-11
GSA:最差值: 1.2087e-15, 最优值: 1.2989e-16, 平均值: 2.882e-16, 标准差: 1.9014e-16, 秩和检验: 3.0199e-11
PSO:最差值: 19.1087, 最优值: 3.5076, 平均值: 10.0904, 标准差: 4.6077, 秩和检验: 3.0199e-11
IWOA:最差值: 5.1602e-263, 最优值: 2.2669e-284, 平均值: 2.3321e-264, 标准差: 0, 秩和检验: 1
函数:F2
WOA:最差值: 0.024008, 最优值: 3.9384e-05, 平均值: 0.0030641, 标准差: 0.0055089, 秩和检验: 5.0922e-08
GWO:最差值: 0.0047574, 最优值: 0.00039995, 平均值: 0.001707, 标准差: 0.00091692, 秩和检验: 4.5043e-11
GSA:最差值: 3.8664, 最优值: 0.054384, 平均值: 0.50863, 标准差: 0.83046, 秩和检验: 3.0199e-11
PSO:最差值: 5.8359, 最优值: 0.06464, 平均值: 0.46507, 标准差: 1.0283, 秩和检验: 3.0199e-11
IWOA:最差值: 0.00056064, 最优值: 1.5912e-05, 平均值: 0.0001771, 标准差: 0.00013844, 秩和检验: 1
函数:F3
WOA:最差值: 5297.0163, 最优值: 0.69439, 平均值: 2239.9459, 标准差: 1707.0238, 秩和检验: 1.0937e-10
GWO:最差值: 9234.8425, 最优值: 4872.8036, 平均值: 6704.4778, 标准差: 867.7088, 秩和检验: 3.0199e-11
GSA:最差值: 10984.8098, 最优值: 8783.0779, 平均值: 10138.2727, 标准差: 495.4127, 秩和检验: 3.0199e-11
PSO:最差值: 10521.9516, 最优值: 8534.0966, 平均值: 9625.5916, 标准差: 512.7198, 秩和检验: 3.0199e-11
IWOA:最差值: 118.607, 最优值: 0.00038205, 平均值: 4.6871, 标准差: 21.6333, 秩和检验: 1
函数:F4
WOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GWO:最差值: 0.037604, 最优值: 0, 平均值: 0.0033049, 标准差: 0.0080497, 秩和检验: 0.011035
GSA:最差值: 38.7027, 最优值: 16.4458, 平均值: 26.7691, 标准差: 5.4199, 秩和检验: 1.2118e-12
PSO:最差值: 18.8852, 最优值: 4.9896, 平均值: 10.7017, 标准差: 3.5421, 秩和检验: 1.2118e-12
IWOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
实验结果表明:改进后的鲸鱼优化算法具有更快的收敛速度和更高的寻优精度。
三、参考文献
[1] 张庆华, 龙伟, 李炎炎, 等. 基于鲸鱼算法优化LSSVM的铣刀磨损监测[J]. 四川大学学报(自然科学版), 2022, 59(1): 68-74.