[学习日志] 白板推导-概率图模型
这里写目录标题
- 背景介绍
-
- 随机变量的基础知识
-
- 加法法则
- 乘法法则
- (以上两个法则是最基础的,其他都来源于此)
- 链式法则
- 贝叶斯法则
- 高维困境
-
- 几种简化方式
-
- 假设相互独立
-
- 朴素贝叶斯分类——基于独立假设
- 马尔可夫链
-
- HMM 隐马尔可夫模型
- 条件独立性假设
- 图
-
- 有向图-贝叶斯网络
- 无向图-马尔可夫网络/马尔可夫随机场
- 贝叶斯网络
-
- 因子分解
- 条件独立性
- D划分
- 马尔可夫毯
- 模型举例
-
- 朴素贝叶斯分类模型
- 高斯混合模型 GMM
- 还有一堆模型,都还没学
- 马尔可夫随机场
-
- 全局马尔可夫性 类似有向图的D划分
- 局部马尔可夫性
- 成对马尔可夫性
- 因子分解
-
- 团&最大团
- 分解式
- Hammesley-Clifford定理
- 势函数
-
- 指数族分布&最大熵原理
- 推断
-
- 变量消除算法
- 置信度传播算法
- Max Product算法
-
- HMM&维特比算法&动态规划
- 算法的内容
- 道德图
-
- 图转化规则
- 道德图性质
- 因子图
背景介绍
随机变量的基础知识
对于多元随机变量X1,X2
P(X1)叫做边缘概率
P(X1,X2)叫做联合概率
P(X1|X2)叫做条件概率
加法法则
乘法法则
(以上两个法则是最基础的,其他都来源于此)
链式法则
贝叶斯法则
![[学习日志] 白板推导-概率图模型_第1张图片](http://img.e-com-net.com/image/info8/f77a697808734911a812285434f4228a.jpg)
圈红的部分是以前语言模型常用的公式
后面是更细致的展开成积分形式
高维困境
以上都是以二维为例子,在高维中计算就会变复杂
比如下图中的联合概率公式,在维度增加时,复杂度呈等差数列求和上升
几种简化方式
假设相互独立
朴素贝叶斯分类——基于独立假设
马尔可夫链
全都独立有点太过理想化,实际应用往往不满足
马尔可夫链的思路就是,某一事件的发生只和前n个事件相关联
(完全相互独立可以说是0阶马尔可夫)

公式是一阶马尔可夫,横竖符号表示独立
也就是说i+1和i之前的项都无关(可能就只和i有关)
HMM 隐马尔可夫模型
条件独立性假设
马尔科夫链也太过理想化,因为可能会有多依赖或跳跃依赖
因此引入条件独行性,公式如下
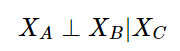
公式中XA,XB,XC都是随机变量的集合,且不相交
集合就能解决多依赖和跳跃依赖的问题
解释一下就是:
在Xc集合中的随机变量确定时,XA,XB集合中的随机变量相互独立
图
通过拓扑排序,就可以很简单的构造一个概率图
有向图-贝叶斯网络
无向图-马尔可夫网络/马尔可夫随机场
贝叶斯网络
因子分解
条件独立性
![[学习日志] 白板推导-概率图模型_第3张图片](http://img.e-com-net.com/image/info8/012bc7c0bd3944c49bacbfba0909cb5f.jpg)
这里用图解释了所谓的条件独立性
也证明了有向图(贝叶斯网络)是包含了条件独立性信息的
上图这种模式的链接,称作tail to tail
可以总结:在尾巴指向的变量前提下,箭头指向的两个随机变量相互独立
![[学习日志] 白板推导-概率图模型_第4张图片](http://img.e-com-net.com/image/info8/dcabde5028c64333a7aa1f995048015d.jpg)
这张图的模式的链接,称作head to tail
可以总结:在中间变量的前提下,两边的两个随机变量相互独立
![[学习日志] 白板推导-概率图模型_第5张图片](http://img.e-com-net.com/image/info8/a27aab4427b34f25945aaf2e29b1c7a2.jpg)
这张图这种模式的链接,称作head to head
可以总结:在c的情况下,ab有关系(即使原本是独立的)
这里ab原本独立很好推,但是ab有关系就很难推
D划分
对于随机变量集合A,B,C
如果满足以下两条件:
- 对于任意a∈A,b∈B,若a,b之间存在顺流(head to tail)或分流(tail to tail)路径时,则中间节点c∈C
- 对于任意a∈A,b∈B,若当a,b之间存在汇流(head to head)路径时,中间节点d不属于C,且d的所有后续节点都不属于C
那么就可以确定A,B,C满足以下条件独立性:
马尔可夫毯
![[学习日志] 白板推导-概率图模型_第6张图片](http://img.e-com-net.com/image/info8/56d68c01602c497ba9015e6207ce72a7.jpg)
然后在分母连乘符号里面把和Xi不相关的项提到积分号外,并且与分子约掉。剩下的部分,就是和Xi相关的。
- Xi出现在Xj的位置,那么式子就和Xi的父母节点相关
- Xi作为某节点的父节点出现在Xparent位置,那么式子就和Xi的子节点相关,并且也将和Xi的配偶节点相关(子节点的其他父节点,如果有的话)
模型举例
朴素贝叶斯分类模型
高斯混合模型 GMM
还有一堆模型,都还没学
马尔可夫随机场
全局马尔可夫性 类似有向图的D划分
对于随机变量集合A,B,C
如果满足以下条件:
- 对于任意a∈A,b∈B,若a,b之间路径时,中间节点c∈C
那么就可以确定A,B,C满足以下条件独立性:
局部马尔可夫性
成对马尔可夫性
因子分解
团&最大团
团:节点的集合,且节点之间都是连通的(有边直接连接)
分解式
![[学习日志] 白板推导-概率图模型_第9张图片](http://img.e-com-net.com/image/info8/44d222ddc5314e9d8519457ad3d9d50d.jpg)
K是最大团的个数
XCi是指团中随机变量组成的集合
Φ是势函数,应该是一个非负函数,常为指数
Z是归一化因子,满足下式:
![[学习日志] 白板推导-概率图模型_第10张图片](http://img.e-com-net.com/image/info8/ad35a8c655fc48519b5f48060ca0a278.jpg)
查阅了一些资料,比较好的是下面这篇:https://blog.csdn.net/qq_23947237/article/details/78387894
这里写一下自己的理解:
- 出发点:马尔可夫链和马尔可夫随机场有某些相似性(都叫马尔可夫)
- 马尔科夫链很好理解,第i个事件只和前n个事件相关(近处相关假设)
- 马尔可夫随机场就不那么好理解了,因为其在空间和时间上都进行了拓展。空间:不再是链式结构,也就是说一个节点可以同时与大于2个节点链接。时间:不再有”前n个“的概念,因为没有箭头了(或者说互为前n)。
- 那么就顺利成章的需要对马尔科夫链的方法做出拓展:将“前n个”拓展为“同团的n个”
Hammesley-Clifford定理
这个定理是说:基于最大团的因子分解方法可以和马尔可夫随机场相互转化
势函数
是函数是人为定义的,只要能尽量模拟真实的情况就可以
这里介绍一种。
![]()
E函数叫做能量函数,来自于统计物理和热力学
当取这个势函数时,X的分布函数P(X)也称作吉布斯分布/玻尔兹曼分布
指数族分布&最大熵原理
当把上述势函数带入分布函数P(X),可以发现P(X)是符合指数族分布的形式的。
根据最大熵原理可知,吉布斯分布/指数族分布具有最大熵
(至于这个最大熵有啥意义,我就不清楚了)
推断
所谓的推断,其实就是求概率。
基本任务主要分以下三种:
- 求边缘概率
- 求条件概率
- 求最大后验概率
方法上则分两种:
- 精确推断
– 变量消除
– 置信度传播(针对树形结构)
– 联合树(针对一般图结构) - 近似推断
– 循环置信度传播(针对有环图)
– 蒙特卡洛推断
– 变分推断
变量消除算法
根据以上概率图,以计算边缘概率为例子,对方法进行说明:
(不确定这个方法是否只能计算边缘概率)
![[学习日志] 白板推导-概率图模型_第11张图片](http://img.e-com-net.com/image/info8/c0c78e3c967546de8257cac500174386.jpg)
核心的规则其实很简单,如下
![[学习日志] 白板推导-概率图模型_第12张图片](http://img.e-com-net.com/image/info8/a9d016b258ff49ba89a67bd9a47d4a55.png)
方法的优点就是简化了计算,缺点如下:
- 不可重用:比如求P(d)之后想求P(a),之前的计算结果都没用,要从头开始
- 顺序:消除变量的顺序会影响到复杂度,顺序错了效果就不好,而在复杂图中很难找到最优的消除顺序
因此该方法只适用简单网络,更多情况下使用其变种
置信度传播算法
置信度传播是为了解决不可重用问题的一种变种
其本质思想就是把VE过程的中间变量进行存储
可以发现,计算过程中有重复的部分(前半部分)
那么可以把这些过程的计算结果储存起来,需要时就通过递推的形式进行计算,就能节省很大的计算量。
下面以无向图为例,开始讲解blief propagation
![[学习日志] 白板推导-概率图模型_第16张图片](http://img.e-com-net.com/image/info8/2206121c80c64f518e7dbb248af62212.jpg)
这里补充一个全类型图的通用联合概率公式,下面的推导都将基于此公式,而非无向图的因子分解(可以认为这个包含了因子分解)
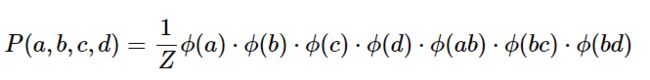
观察上式1,发现其具有递推结构,故对此做出归纳如下:
![[学习日志] 白板推导-概率图模型_第18张图片](http://img.e-com-net.com/image/info8/f6d4930f64d84688b5558c8c3e8ccf40.jpg)
其中NB(j)-i是指节点j的所有相连节点,除i节点以外。
也就是说,变量节点j的消除式是由其相连节点的消除式递推而来的。
而所谓的BP算法,其实就是先求所有mij,之后根据mij求边缘概率。
下面是详细的说明,BP算法可共分为三步:
- 选择一个节点作为根节点(因为是无向图,下图以a为根)
- 收集消息(对应下图蓝色箭头,使用递推式子进行计算)
- 分发消息(对应下图红色箭头,使用递推式子进行计算)
BP算法还有一种并行式的阐述,是激发后广播的机制,并动态更新。
好处是分布式的进行运算,提高运行效率。
Max Product算法
HMM&维特比算法&动态规划
![[学习日志] 白板推导-概率图模型_第21张图片](http://img.e-com-net.com/image/info8/585279c04395409e96c911ba59351077.jpg)
维特比算法可以看作是为了求解上述最短路径问题的。
维特比算法的核心就是删除部分”不可能路径“
参考:https://www.zhihu.com/question/20136144
算法的内容
改进方法:Sum-Product改为Max-Product
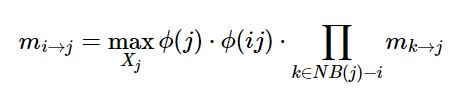
关于上式的理解:
- 在BP算法中,最终目的是求边缘概率,因此为了消除变量使用SumProduct
- 在MaxProduct算法中,目的不是消除变量,而是找到各个变量”最佳状态“,因此使用了MaxProduct
- 在获取”最佳状态“的过程中使用了递归的思想,即当前节点的最佳状态是依赖于相连节点的最佳状态的(结合维特比算法)
这里容易导致困惑的地方在于:

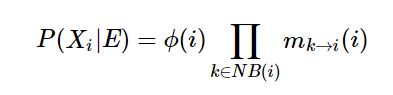
这两个公式哪个是对的?
其实都是对的,因为是用因子式展开的(感觉因子式是很万能的,这个因子不是因子分解那个,是因子图的那个)。区别在于要不要消除E
道德图
这个概念产生的原因是因为,人们希望把有向图转为无向图(一般化)
由有向图转换得到的无向图被称为道德图
图转化规则
这个是从形式上进行推导出来的
道德图性质
在道德图中体现的条件独立性在有向图中也是成立的
因子图
因为在进行道德图转换的时候,可能会有环产生(汇流结构)
而Blief Propagation算法是不适用环结构的,因子图可以很好的解决掉环的问题
因子式:

其中s是原图(无向图或有向图)的任意非空子集
Xs是子集对应的集合
个人理解:根据有向图和无向图的因子分解式进行了共同抽象,从而得到的图
- 有向图的因子分解式 和 无向图的因子分解式 都是由因子构成的
- 因子都可以抽象看作一个关于部分节点的函数,比如有向图的因子就是以父节点和子节点作为输入变量的函数(父子节点都是子集),而无向图势函数本身就是一种函数(最大团也是子集),二者都能被因子公式囊括
- 那么二者就可以通过一个共同的抽象式子进行表示了
- 再将这些“抽象函数”画在图上就ok了
可以参考:https://blog.csdn.net/qq_23947237/article/details/78389188



![[学习日志] 白板推导-概率图模型_第2张图片](http://img.e-com-net.com/image/info8/3a1e6302643249d0898a050920d3bc71.png)


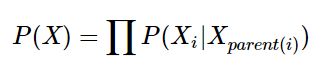

![[学习日志] 白板推导-概率图模型_第7张图片](http://img.e-com-net.com/image/info8/7afb4e31b78f41eca28cb6abf33c6f2a.jpg)
![[学习日志] 白板推导-概率图模型_第8张图片](http://img.e-com-net.com/image/info8/d43779902e5c468982c4d566769b5df2.jpg)
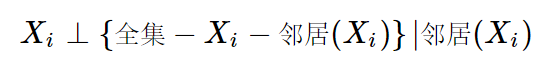



![[学习日志] 白板推导-概率图模型_第13张图片](http://img.e-com-net.com/image/info8/49ede92855d84a42a26ab6d6a6cbc120.jpg)
![[学习日志] 白板推导-概率图模型_第14张图片](http://img.e-com-net.com/image/info8/aabb8c18500646f3b52bb3d1118f8095.jpg)
![[学习日志] 白板推导-概率图模型_第15张图片](http://img.e-com-net.com/image/info8/63f22d7147b5463facb776f430c2498e.jpg)
![[学习日志] 白板推导-概率图模型_第17张图片](http://img.e-com-net.com/image/info8/84609a97872d4d40805d90ad9cd3ce22.jpg)
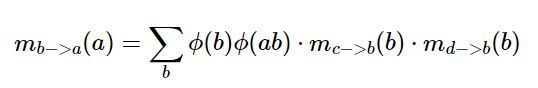

![[学习日志] 白板推导-概率图模型_第19张图片](http://img.e-com-net.com/image/info8/e0d13a6e06ba4a6bb2f9cda496ee78a5.jpg)
![[学习日志] 白板推导-概率图模型_第20张图片](http://img.e-com-net.com/image/info8/a2210bf83da54b11b7b059aa6e97abc0.jpg)

![[学习日志] 白板推导-概率图模型_第22张图片](http://img.e-com-net.com/image/info8/0fb42e9e186644f684582f840f5555c8.jpg)