最小二乘法拟合平面原理MATLAB&C++实现
文章目录
- 最小二乘法拟合平面原理MATLAB&C++实现
-
- 最小二乘法拟合平面原理
- MATLAB实现
- c++实现
最小二乘法拟合平面原理MATLAB&C++实现
最小二乘法拟合平面原理
最小二乘法是我们平时用的比较的多一种拟合算法,尤其是在直线拟合,平面拟合中,大量的工程实践验证了其具有简便好用的特点。但是,其抗噪声性差,对测量数据有较高的要求。下面我们探讨一下其基本原理和实现过程。
首先,我们会用各种仪器测量得到多组数据。当然,至少要有不同的三组数据,且不能在同一条直线上取这些数据,这是确定一个平面的基本要求。
我们选择平面方程为:
ax + by + cz + d = 0
为了方便构建误差函数,我们转换形式,我们可以用下面方程表示:
z = ax + by + c
我们构建最小二乘误差函数:
当误差函数取得最小值时,我们就得到了最佳拟合的平面。
视a,b,c为自变量,我们对其求导,得到如下方程组:
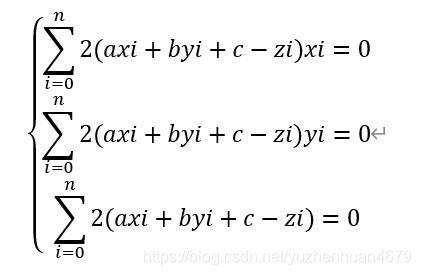
移项,整理可得:
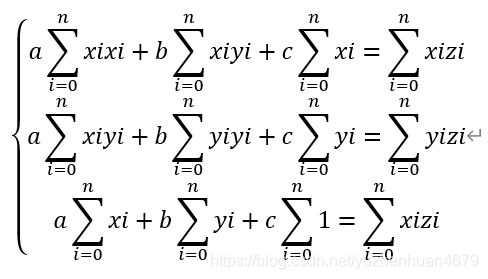
为了方便求解,我们用矩阵的形势来表示上述方程组,
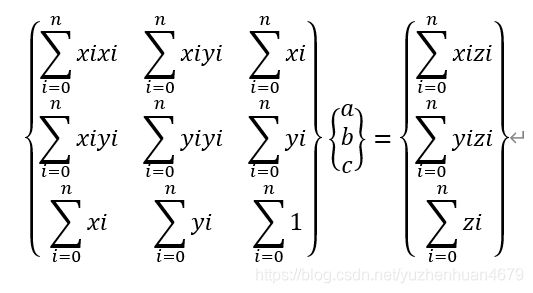
转变形势,得到a,b,c的表达式:

将测量数据带入上式,即可求出a,b,c的值。
MATLAB实现
clc;
clear all;
x = [1478.5,1190.5,2043];
y = [968.5,1449.5,1432];
z = [33202.83,33185.18,33168.82];
a12 = sum(xy’);
a13 = sum(x);
a22 = sum(y.^2);
a23 = sum(y);
a33 = size(x,2);
c11 = sum(xz’);
c22 = sum(yz’);
c33 = sum(z);
A = [a11 a12 a13;
a12 a22 a23;
a13 a23 a33];
B = inv(A);
C = B[c11;c22;c33];
c++实现
int n = cloud_.size();
Eigen::MatrixXd points;
points.resize(n, 3);
for (int i = 0; i < n; i++)
{
points(i, 0) = cloud_.at(i).x;
points(i, 1) = cloud_.at(i).y;
points(i, 2) = cloud_.at(i).z;
}
double A11 = 0, A12 = 0, A13 = 0;
double A21 = 0, A22 = 0, A23 = 0;
double A31 = 0, A32 = 0, A33 = 0;
double B1 = 0, B2 = 0, B3 = 0;
A11 = (points.array().col(0) * points.array().col(0)).sum();
A12 = (points.array().col(0) * points.array().col(1)).sum();
A13 = (points.array().col(0)).sum();
A21 = A12;
A22 = (points.array().col(1) * points.array().col(1)).sum();
A23 = (points.array().col(1)).sum();
A31 = A13; A32 = A23;
A33 = n;
B1 = (points.array().col(0) * points.array().col(2)).sum();
B2 = (points.array().col(1) * points.array().col(2)).sum();
B3 = (points.array().col(2)).sum();
Eigen::MatrixXd A;
A.resize(3, 3);
A(0, 0) = A11; A(0, 1) = A12; A(0, 2) = A13;
A(1, 0) = A21; A(1, 1) = A22; A(1, 2) = A23;
A(2, 0) = A31; A(2, 1) = A32; A(2, 2) = A33;
Eigen::MatrixXd B;
B.resize(3, 1);
B(0, 0) = B1; B(1, 0) = B2; B(2, 0) = B3;
double C1 = 0, C2 = 0, C3 = 0;
C1 = A.inverse()(0, 0) * B(0) + A.inverse()(0, 1) * B(1) + A.inverse()(0, 2) * B(2);
C2 = A.inverse()(1, 0) * B(0) + A.inverse()(1, 1) * B(1) + A.inverse()(1, 2) * B(2);
C3 = A.inverse()(2, 0) * B(0) + A.inverse()(2, 1) * B(1) + A.inverse()(2, 2) * B(2);

