在BSV上运行深度神经网络
我们已经实现了一个用于手写数字分类的深度神经网络。已经训练好的模型完全在链上运行。它使用手写数字的 MNIST 数据集进行离线训练。该模型采用 28x28 灰度像素的图像并输出 0 到 9 的数字。
深度神经网络简介
人工神经网络是受生物神经网络启发而构建的。网络通过接触大量带标签的数据示例来学习。这个过程也称为监督学习。
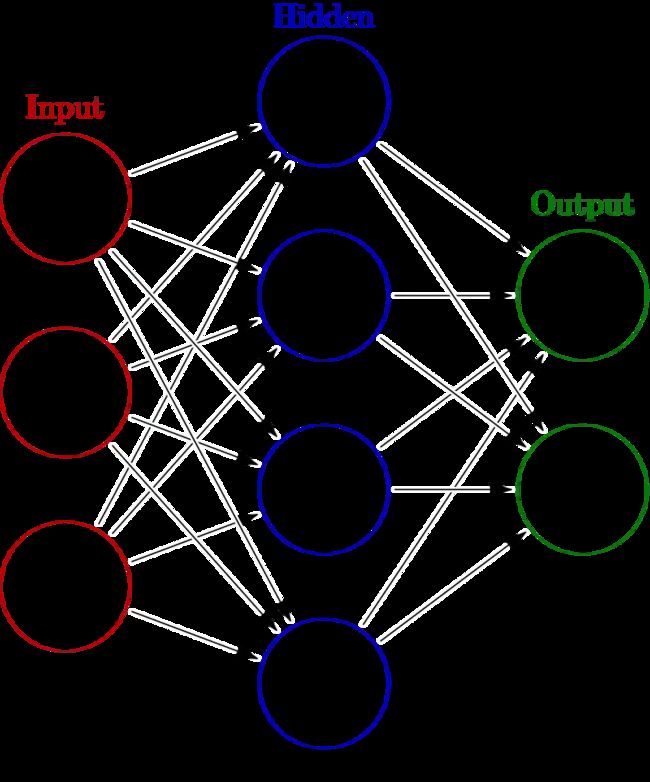
该网络由几个组件组成:神经元/节点、连接、偏差和激活函数。这些组件被连续分组到层中。第一层称为“输入层”,数据通过该层传入网络,最后一层称为“输出层”,网络通过该层返回其输出。一个非常简单的神经网络只包含这两层。为了提高性能,我们可以在两者之间添加一个或多个“隐藏层”。具有隐藏层的网络称为“深度神经网络”(DNN)。
网络中神经元之间的每个连接都用特定值加权。每个神经元还有一个称为“偏差”的值,该值会添加到其输入的总和中。学习是找到一组这些权重和偏差的过程,这样网络将在给定一些输入的情况下返回有意义的输出。
为了直观地了解深层神经网络的工作原理,我们建议您观看有关该主题的短视频系列。
网络架构
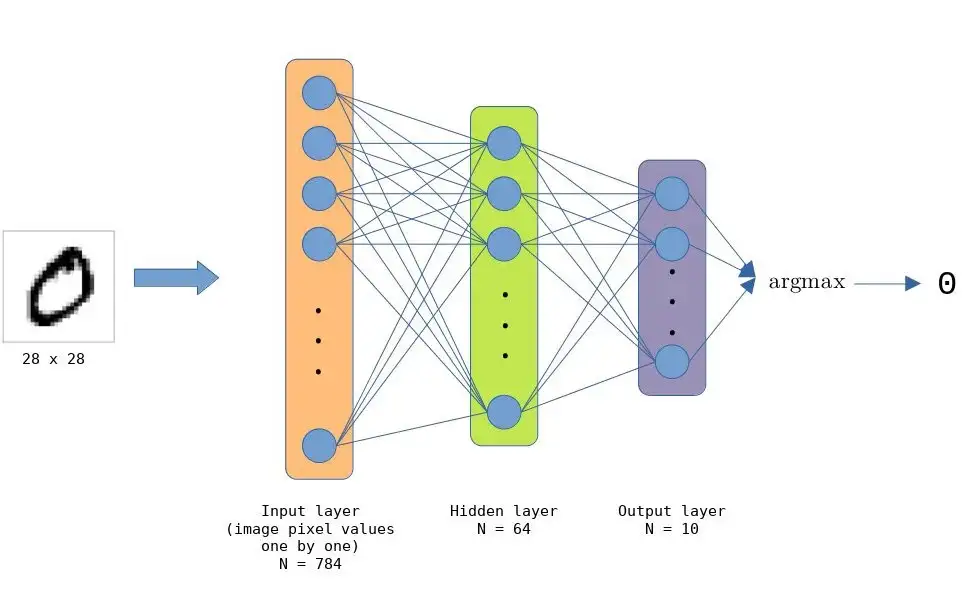
MNIST 手写数字的 DNN 由 784 (28 x 28) 个节点的输入层、64 个节点的隐藏层和 10 个节点的输出层(可能的类/数字的数量)组成。这些层都是全连接的,这使得网络总共包含 501760 (784 * 64 * 10) 个连接。
隐藏层中的节点使用 ReLU 激活函数。 Argmax 用于输出节点以获得正确的值,即分类的数字。
训练模型
DNN 使用 Keras 进行训练。通过我们概述的网络架构并使用 RMSprop 优化器进行训练,该模型能够在 50 个时期后达到 98% 的分类准确率。
import numpy as np
from tensorflow import keras
from tensorflow.keras import layers
# Model / data parameters
num_pixels = 28 * 28
num_nodes_hl = 64
num_classes = 10
batch_size = 469
epochs = 50
# Load the data and split it between train and test sets.
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
# Reshape images to [784, 1] and scale them to the [0, 1] range.
x_train = x_train.reshape(x_train.shape[0], num_pixels).astype("float32") / 255
x_test = x_test.reshape(x_test.shape[0], num_pixels).astype("float32") / 255
# Model
model = keras.Sequential([layers.Dense(num_nodes_hl, activation="relu"),
layers.Dense(num_classes, activation="softmax")
])
model.compile(loss="sparse_categorical_crossentropy", optimizer="rmsprop", metrics=["accuracy"])
model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.1)
训练模型后,必须以我们可以在 sCrypt 智能合约中使用的格式来导出权重和偏差。出于性能原因,我们将这些值编码为 bytes 字节,而不是数组。
实现
我们已经实现了上面的 DNN,类似于我们之前实现的单层神经网络(又名感知器)。完整的代码可以在 GitHub 上找到。
import "../train/modelParams.scrypt";
library Model {
static function applyWeights0(int[ModelParams.N_INPUTS] in) : int[ModelParams.N_NODES_HL] {
int[ModelParams.N_NODES_HL] res = repeat(0, ModelParams.N_NODES_HL);
loop (ModelParams.N_NODES_HL) : i {
int sum = 0;
loop (ModelParams.N_INPUTS) : j {
sum += (ModelParams.getWeight0(i, j) * in[j]) / 100000000;
}
res[i] = sum;
}
return res;
}
static function applyWeights1(int[ModelParams.N_NODES_HL] in) : int[ModelParams.N_NODES_OUT] {
int[ModelParams.N_NODES_OUT] res = repeat(0, ModelParams.N_NODES_OUT);
loop (ModelParams.N_NODES_OUT) : i {
int sum = 0;
loop (ModelParams.N_NODES_HL) : j {
sum += (ModelParams.getWeight1(i, j) * in[j]) / 100000000;
}
res[i] = sum;
}
return res;
}
static function addBiases0(int[ModelParams.N_NODES_HL] in) : int[ModelParams.N_NODES_HL] {
int[ModelParams.N_NODES_HL] res = repeat(0, ModelParams.N_NODES_HL);
loop (ModelParams.N_NODES_HL) : i {
res[i] = in[i] + ModelParams.getBias0(i);
}
return res;
}
static function addBiases1(int[ModelParams.N_NODES_OUT] in) : int[ModelParams.N_NODES_OUT] {
int[ModelParams.N_NODES_OUT] res = repeat(0, ModelParams.N_NODES_OUT);
loop (ModelParams.N_NODES_OUT) : i {
res[i] = in[i] + ModelParams.getBias1(i);
}
return res;
}
static function applyReLU(int[ModelParams.N_NODES_HL] in) : int[ModelParams.N_NODES_HL] {
int[ModelParams.N_NODES_HL] res = repeat(0, ModelParams.N_NODES_HL);
loop (ModelParams.N_NODES_HL) : i {
int inVal = in[i];
if (inVal > 0) {
res[i] = inVal;
}
}
return res;
}
static function predict(int[ModelParams.N_INPUTS] inputs) : int {
int[ModelParams.N_NODES_HL] step0 = applyWeights0(inputs);
int[ModelParams.N_NODES_HL] step1 = addBiases0(step0);
int[ModelParams.N_NODES_HL] step2 = applyReLU(step1);
int[ModelParams.N_NODES_OUT] step3 = applyWeights1(step2);
int[ModelParams.N_NODES_OUT] step4 = addBiases1(step3);
int idxMaxVal = 0;
int maxVal = step4[0];
loop (ModelParams.N_NODES_OUT) : i {
int outVal = step4[i];
if (outVal > maxVal) {
idxMaxVal = i;
maxVal = outVal;
}
}
return idxMaxVal;
}
}
函数 predict() 接受输入层的初始值。在我们的例子中,这是手写图像的序列化值。它返回一个代表分类结果的整数,即图像上的数字。
因为 sCrypt 不支持原生浮点数,所以我们通过简单地将值缩放 10⁸ 来使用定点表示。例如,0.86758491 变成整数 86758491。当将两个值相乘时,我们重新缩放结果,即除以 10⁸。
潜在用例
像这样的 DNN 可以在智能合约中以多种方式使用。例如,您可以训练模型以一定的准确度识别图像中是否包含热狗。鼓励用户在互联网上搜索此类照片,并自动通过提交这些照片获得比特币小额支付。可以收集这些照片来训练模型并提高其准确性。