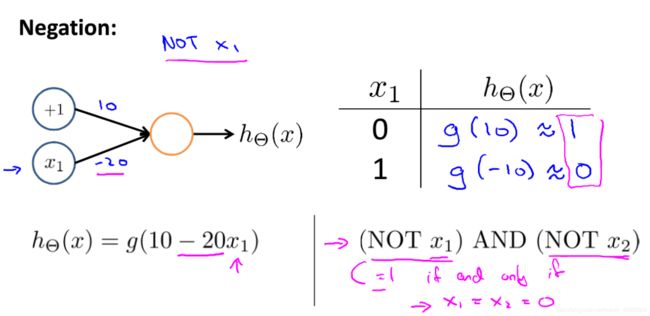吴恩达机器学习课程笔记——Ch9 神经网络
Chapeter 9 Neural Networks（神经网络：示例）
已经不能倍速看了==真实....
课程笔记总览传送门：https://blog.csdn.net/weixin_42900928/article/details/86523192
目录
Chapeter 9 Neural Networks（神经网络：示例）
9.1 Non-linear Hypotheses（非线性假设）
9.2 Model Representation（模型展示）
9.3 Examples and Intuitions（例子和直观解释）
9.4 Multiclass Classification（多类分类）
9.1 Non-linear Hypotheses（非线性假设）
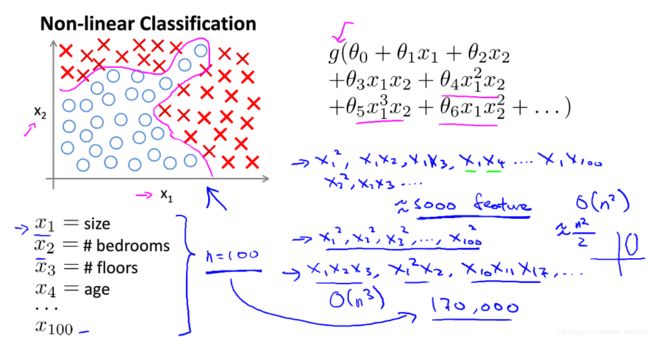
逻辑回归就是非线性假设，那么为什么要单独开一节呢？
首先，非线性假设肯定不止一种；其次，逻辑回归在模型不复杂的情况下还能用，但模型复杂程度上去后就会有计算方面的问题：
图 1-1 逻辑回归的问题
在只有两个变量x1、x2时，项数可以不多。但如果有100个变量时，二次的有约5000项、三次的更是超多，这时计算就会受阻。
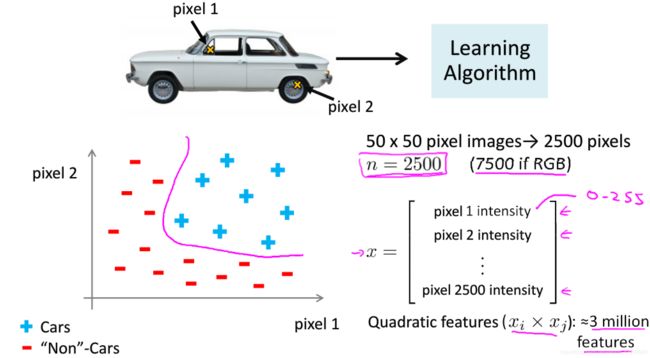
举个例子：
图 1-2 像素问题
一张50 x 50 像素的图片有2500个像素点（RGB，7500），就算只考虑二次项，它也会有约3百万个特征，这计算起来太慢了。
当遇到这种非线性假设时，需要新的知识更高效、快速的处理。也就是神经网络。
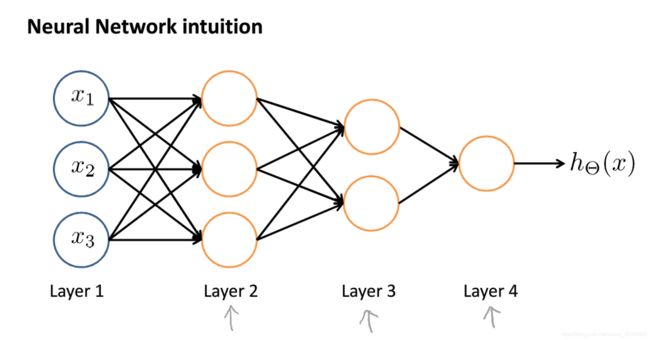
9.2 Model Representation（模型展示）
图 2-1 真·神经网络
简单说就是：输入神经元→神经元计算(处理)→传输进新神经元(当作输入)→神经元计算(处理)→...→输出。
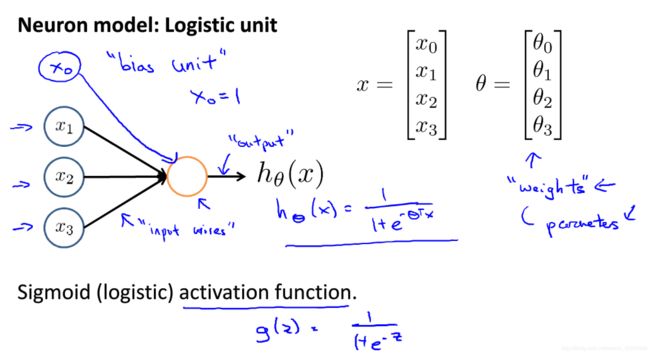
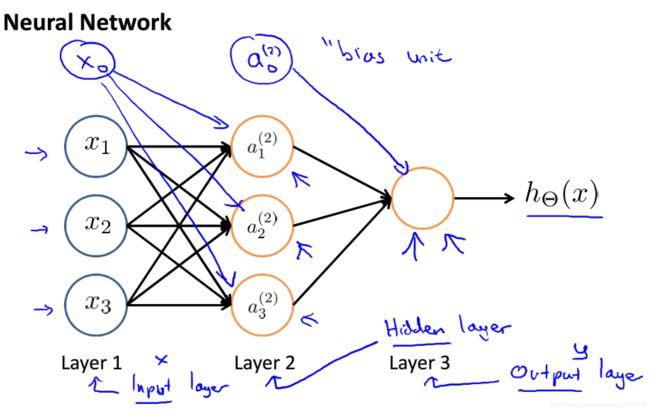
在计算机上运行的神经网络是什么样子的呢？先举一个简单的例子：
图 2-2 神经网络（一）
可以看出，神经网络似乎还是逻辑回归。
注：向量 
即可以继续被称为“参数”，也可以称为“权重”；x0称为“bias unit”=1，看情况决定加不加。
深入一些：
图 2-3 神经网络（二）
相比图2-2，图2-3的神经网络多了一层，引入层的概念：x为输入层，y（预测值,= 
）为输出层，中间的都是(这里只有1层)隐藏层。
注：上标可理解为处在第几层，下标就是排序（如 
代表第二层的第一个值）； 变成了 
，代表向量变成了矩阵，后面会提。
再深入一些，关键1：
图 2-4 模型解读
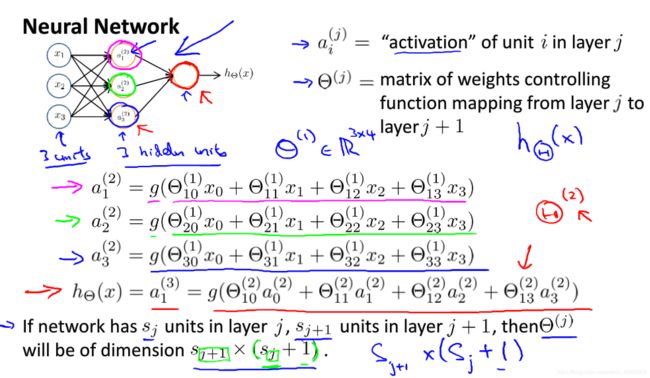
以图2-3的三层网络为例，做出如下解释：
—— 
称为“activation”(激活项)，这里的 j 代表所在的层数；
—— 
是前一层向后一层推进(计算)过程中用到的参数(权重)矩阵,，矩阵的内容如图，由g(z)的存在，得知这依旧是逻辑回归，这里的 j 代表所在层数的上一层，即 j = 层数 - 1。 不存在任何一层，它是一个中间过程，可以当作它在通道（线）中。
——最后2行关于 维数的例子，比如要看 
，就看第 1 层也就是向量 x 的项数（ 
=3）和第 2 层 
的项数（ 
=3），即3( ) x （3+1=）4( + 1)。
关键2：
图 2-5 模型简化
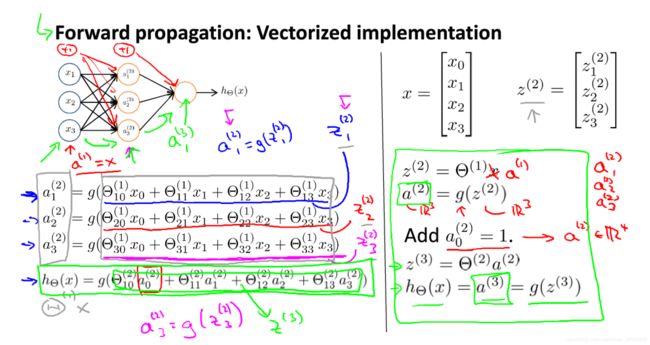
图2-4的模型太过复杂，尤其是参数量上去了以后，为了后续的处理，模型简化是十分必要的：
——首先令向量 x = 
；令 
= 
，因此， 
= 
；
—— 
。
实例如右半部分所示。
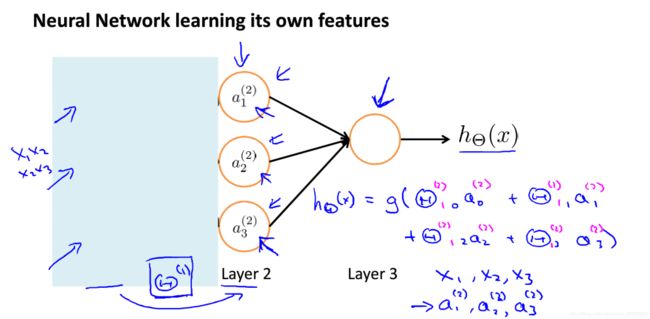
介绍完模型，再看看神经网络的本质：
图 2-6 神经网络的本质
如图，神经网络就是一个自己训练特征的，并用这些新特征进行逻辑回归的模型，这个过程称为向前传播。
9.3 Examples and Intuitions（例子和直观解释）
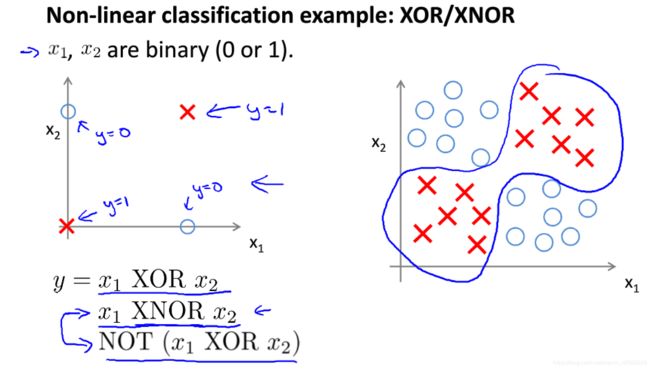
最终目标是解释一个较复杂的XNOR（0、1分类）：
图 3-1 XNOR
要想知道神经网络如何实现对左半部分的处理，要从几个简单的例子入手。
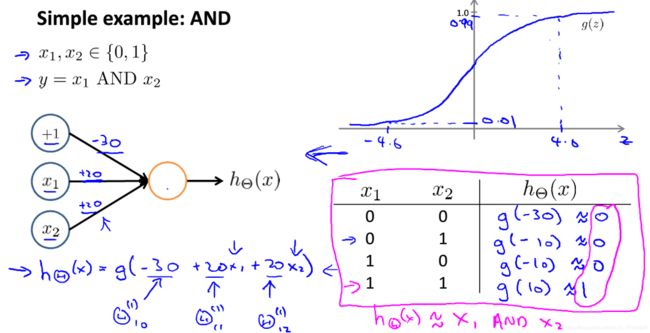
AND:
图 3-2 AND
OR:
图 3-3 OR
NOT:
图 3-4 NOT
从图3-2、3、4可以看出，训练神经网络是通过改变、赋予参数(权重)来达到目的的过程。
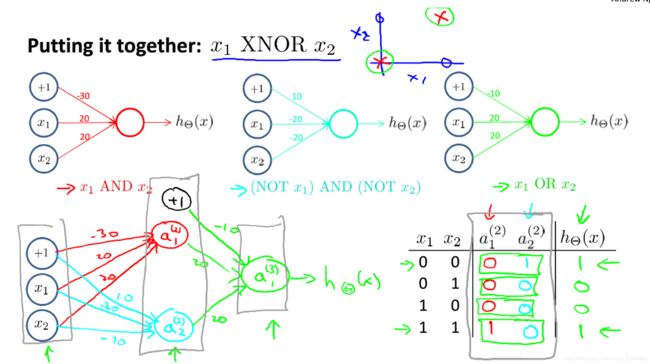
最后，看一下XNOR：
图 3-5 XNOR
复杂如斯。
图 3-6 神经网络（三）
综上，神经网络是一层比一层的存在，由简到繁，逐步深入。
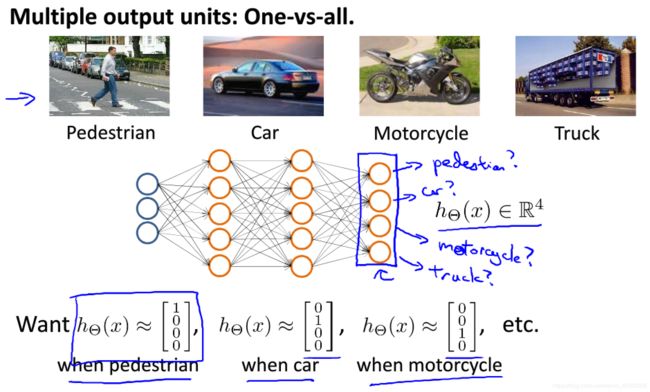
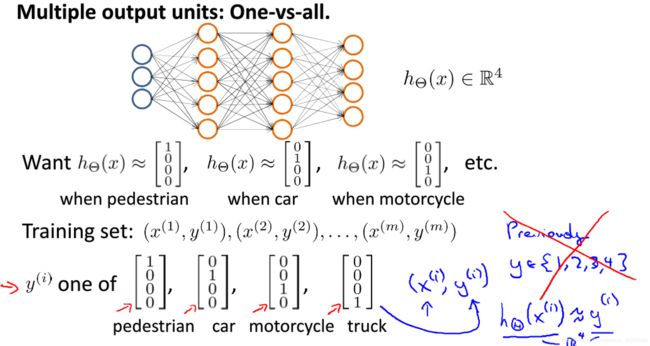
9.4 Multiclass Classification（多类分类）
图 4-1 多类分类
是 One-vs-all 的延伸。
图 4-2 多类分类的输出