哈夫曼树构造与编码

目录

一、哈夫曼树是什么？

二、哈夫曼树的构造过程

1.过程分析

2.过程代码实现

Select函数

三、哈夫曼编码的实现

完整代码

总结

---

一、哈夫曼树是什么？

哈夫曼树是又称最优树，是一类带权路径长度最短的树，在实际应用有着广泛的应用。哈夫曼树的定义，涉及路径、路径长度、权等概念。

---

二、哈夫曼树的构造过程

1.过程分析

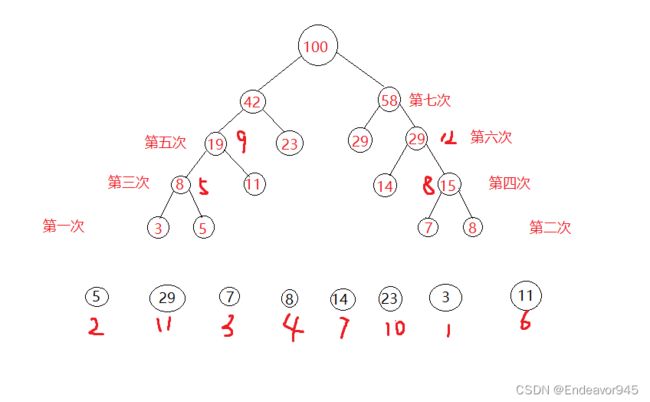
1、从一片森林中寻取到两棵节点权值最小的树作为左右子树构造一棵新的二叉树，并且已经选过的树不再进行选取

2、将新构造的二叉树与森林中的树再次进行比较，重复1过程

3、最后合并成为一棵二叉树

2.过程代码实现

        首先是初始化一棵二叉树，用来储存接下来要构造的二叉树。初始化的过程中应该动态申请2n个单元，然后循环2n-1次将单元中的所有都初始化为0

        其次是将森林中的树的权值储存到所创建的树中

        然后开始创建哈夫曼树

代码如下：

void CreateHaffmanTree(HaffmanTree &ht,int n)
{
	if (n <= 1) return ;
	int m = 2 * n - 1;
	ht = (HaffmanTree)malloc(sizeof(htNode)*(m+1));
	for (int i = 1; i <= m; i++)//初始化双亲结点和孩子节点的值
	{
		ht[i].parent = 0;
		ht[i].lchild = 0;
		ht[i].rchild = 0;
	}
	for (int i = 1; i <= n; i++)//将权值进行存储
	{
		int x;
		scanf("%d", &x);
		ht[i].weight = x;
	}
	//开始创建哈夫曼树
	for (int i = n+1; i <= m; i++)
	{
		int l=0, r=0;
		Select(ht, i-1, l,  r);//调用Select函数返回最小的两颗树的权值，并且返回下标
		ht[i].weight = ht[l].weight + ht[r].weight;
		ht[i].lchild = l;//将返回的下标作为新构造树的的左右孩子
		ht[i].rchild = r;
		ht[l].parent = i;//将新构造树的结点作为最小的两个树的双亲结点
		ht[r].parent = i;
	}
	visit(ht,m);
}

Select函数

通过此函数返回最小的两个树的权值和下标

代码如下：

void Select(HaffmanTree ht, int n, int &l, int &r)//此函数用于返回权值最小的两个数，并且返回这两个数的节点作为孩子节点
{
	int min1 = 9999999;
	int min2 = 999999;

	for (int i = 1; i <= n; i++)
	{
		if (ht[i].weight < min1 && ht[i].parent == 0)//返回最小的权值的节点作为左孩子
		{
			min1 = ht[i].weight;
			l = i;
		}
	}
	for (int i = 1; i <= n; i++)
	{
		if (ht[i].weight < min2 && ht[i].parent == 0)//返回第二小的权值的节点作为右孩子
		{
			int t = i;
			if (l!=t)//在这里卡了好久，没想到用下标来判断一组数据中最小的两个数
			{
				min2 = ht[i].weight;
				r = i;
			}
		}
	}
}

三、哈夫曼编码的实现

        构造哈夫曼树之后，求哈夫曼编码的主要思路：依次以叶子节点为出发点，向上回溯至根节点为止。回溯是规定左孩子为0有孩子为1

        由于每个哈夫曼编码是变长编码，因此使用一个指针来存放每个字符串编码的首地址。

代码如下：

void CreatHaffmanCode(HaffmanTree ht, HaffmanCode& hc, int n)
{
	hc = (HaffmanCode)malloc(sizeof(char*) * (n + 1));//分配存储n个编码的空间，其实用不到n个空间，但是为了想用的时候有，直接开辟n个空间就行
	char *cd = (char*)malloc(sizeof(char) * n);  //分配临时存放字符编码的动态数组空间
	cd[n - 1] = '\0';  //编码结束符
	for (int i = 1; i <= n; i++)
	{
		int start = n - 1;//回溯的过程是由下往上的，所以存储的时候直接由后往前存
		int c = i;//标记点，用来判断左右孩子
		int f = ht[i].parent;//f直接指向c的双亲结点，
		while (f!=0)
		{
			start--;
			if (ht[f].lchild == c)//找到第一个节点的双亲结点后判断左右孩子
			{
				cd[start] = '0';
			}
			else
			{
				cd[start] = '1';
			}
			c = f; 
			f = ht[f].parent;//递归的思想，继续往上回溯
		}
		hc[i] = (char*)malloc((n - start) * sizeof(char));//为第i个字符分配空间，即为了保存第i个字符的编码
		strcpy(hc[i], &cd[start]);//将求到的编码复制到ht空间去
	}
	free(cd);//释放临时空间
	visitCode(ht, hc, n);//开始打印
}

完整代码

#define _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
#include 
typedef struct
{
	int weight;
	int parent;
	int lchild;
	int rchild;
}htNode, * HaffmanTree;

typedef char** HaffmanCode;

void Select(HaffmanTree ht, int n, int &l, int &r)//此函数用于返回权值最小的两个数，并且返回这两个数的节点作为孩子节点
{
	int min1 = 9999999;
	int min2 = 999999;

	for (int i = 1; i <= n; i++)
	{
		if (ht[i].weight < min1 && ht[i].parent == 0)//返回最小的权值的节点作为左孩子
		{
			min1 = ht[i].weight;
			l = i;
		}
	}
	for (int i = 1; i <= n; i++)
	{
		if (ht[i].weight < min2 && ht[i].parent == 0)//返回第二小的权值的节点作为右孩子
		{
			int t = i;
			if (l!=t)//在这里卡了好久，没想到用下标来判断一组数据中最小的两个数
			{
				min2 = ht[i].weight;
				r = i;
			}
		}
	}
}

void visit(HaffmanTree ht, int m)
{
	for (int i = 1; i <= m; i++)
	{
		printf("%-12d%-12d%-12d%-12d\n", ht[i].weight, ht[i].parent, ht[i].lchild, ht[i].rchild);
	}
}

void CreateHaffmanTree(HaffmanTree &ht,int n)
{
	if (n <= 1) return ;
	int m = 2 * n - 1;
	ht = (HaffmanTree)malloc(sizeof(htNode)*(m+1));
	for (int i = 1; i <= m; i++)//初始化双亲结点和孩子节点的值
	{
		ht[i].parent = 0;
		ht[i].lchild = 0;
		ht[i].rchild = 0;
	}
	for (int i = 1; i <= n; i++)//将权值进行存储
	{
		int x;
		scanf("%d", &x);
		ht[i].weight = x;
	}
	//开始创建哈夫曼树
	for (int i = n+1; i <= m; i++)
	{
		int l=0, r=0;
		Select(ht, i-1, l,  r);
		ht[i].weight = ht[l].weight + ht[r].weight;
		ht[i].lchild = l;
		ht[i].rchild = r;
		ht[l].parent = i;
		ht[r].parent = i;
	}
	printf("初始权值    双亲结点    左孩子    右孩子\n");
	visit(ht,m);
}


void visitCode(HaffmanTree ht, char**hc,int n)
{

	printf("--------------------哈夫曼树的编码-------------------\n");
	printf("初始权值  哈夫曼编码\n");
	for (int i = 1; i <= n; i++)
	{
		printf("%-12d%-12s%\n", ht[i].weight, hc[i]);
	}
}


void CreatHaffmanCode(HaffmanTree ht, HaffmanCode& hc, int n)
{
	hc = (HaffmanCode)malloc(sizeof(char*) * (n + 1));//分配存储n个编码的空间，其实用不到n个空间，但是为了想用的时候有，直接开辟n个空间就行
	char *cd = (char*)malloc(sizeof(char) * n);  //分配临时存放字符编码的动态数组空间
	cd[n - 1] = '\0';  //编码结束符
	for (int i = 1; i <= n; i++)
	{
		int start = n - 1;//回溯的过程是由下往上的，所以存储的时候直接由后往前存
		int c = i;//标记点，用来判断左右孩子
		int f = ht[i].parent;//f直接指向c的双亲结点，
		while (f!=0)
		{
			start--;
			if (ht[f].lchild == c)//找到第一个节点的双亲结点后判断左右孩子
			{
				cd[start] = '0';
			}
			else
			{
				cd[start] = '1';
			}
			c = f; 
			f = ht[f].parent;//递归的思想，继续往上回溯
		}
		hc[i] = (char*)malloc((n - start) * sizeof(char));//为第i个字符分配空间，即为了保存第i个字符的编码
		strcpy(hc[i], &cd[start]);//将求到的编码复制到ht空间去
	}
	free(cd);//释放临时空间
	visitCode(ht, hc, n);//开始打印
}

int main()
{
	HaffmanTree ht;
	HaffmanCode hc;
	int n ;
	printf("请输入n个数的权值: ");
	scanf("%d", &n);
	printf("--------------------哈夫曼树的构造-------------------\n");
	printf("请输入每个数的权值：");
	int l = 0, r = 0;
	CreateHaffmanTree(ht, n);
	printf("\n");
	CreatHaffmanCode(ht, hc, n);
	return 0;
}

---

总结

以上就是对哈夫曼树构造以及编码的实现，在这个过程也发现了许多问题，比如比较大小的时候竟然不知道用下标比较，整个过程下来也是学到了很多东西