轮式里程计与激光雷达进行标定2--里程计运动学模型方法（理论+实现代码）

轮式里程计定义

什么是轮式里程计:
利用轮子转速来测量机器人行程的装置
原理如下图,简单直接

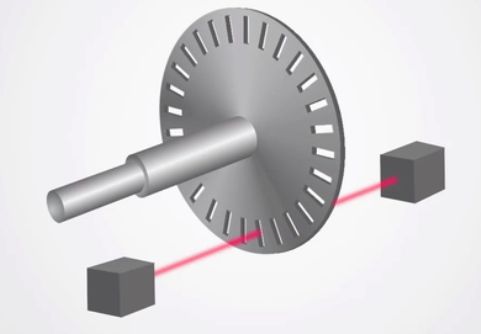
实物就张这个样子

机器人领域通常使用光电编码器来测量轮子转速,轮子转动时光电编码器接收到脉冲信号,脉冲数乘以系数可以得
知轮子转了多少圈。

两轮机器人,通过轮速不断的积分运算,可以得知机器人前进了多少,同时可以利用两轮速之差,算出机器人转了
多少度,从而实现机器人的航迹推算定位。

轮式里程计与激光SLAM的关系

激光SLAM的其中的一个步骤进行帧间匹配时就是通过两个时刻的点云匹配得到这两个时刻的相对位姿。

上面说了轮式里程计也可以通过统计电机的转速来计算得到机器人的位姿.

既然都可以得到位姿,那么就又涉及到了多传感器融合的问题了,谈到融合必然各传感器有各自的优缺点

激光SLAM在对于环境几何特征点少的情况下不适用,比如长走廊的情况下,显然轮式里程计和这个情况没有关系
轮式里程计在出现路面打滑情况下则会出现累计误差,显然激光SLAM不会有这种情况.既然两者各有各的长处,就融合呗.

融合的思想如下:
轮式里程计的定位可以为激光SLAM提供两个时刻之间匹配的初值,初值准确的情况下可以提升激光SLAM的精度。
此外,轮式里程计可以单独实现短距离航迹推算定位,激光SLAM也可以实现定位,两者融合可以加强定位的准确
性和鲁棒性.

轮式里程计标定前言

轮式里程计的基本原理就是利用两轮速之差,算出机器人转了多少度。这一前提是,已知车轮半径以及两轮间距。

所以在一下情况下需要对轮式里程计进行标定

• 轮速计硬件变形
• 车轮半径以及两轮间距发生变化
• 脉冲信号到轮速转换系数不准

标定方法可以分为两类

• 白盒标定:在已知传感器物理模型时,需要采用基于模型的方法
• 黑盒标定:在不知道传感器物理模型时,可尝试直接线性方法

轮式里程计与激光雷达标定数学建模

这里主要说的是两轮差速底盘的运动学模型

一般的室内机器人用这种,优势是

• 结构简单
• 成本低
• 模型简单

在设计标定的数学模型时,首先要确定已知哪些量
通过激光传感器的匹配结果可以知道 x位移 y位移 角度
通过轮速里程计可以得到两个轮子的旋转角速度.
那么也就是需要通过轮子的角速度,表示里程计计算的 x位移 y位移 角度

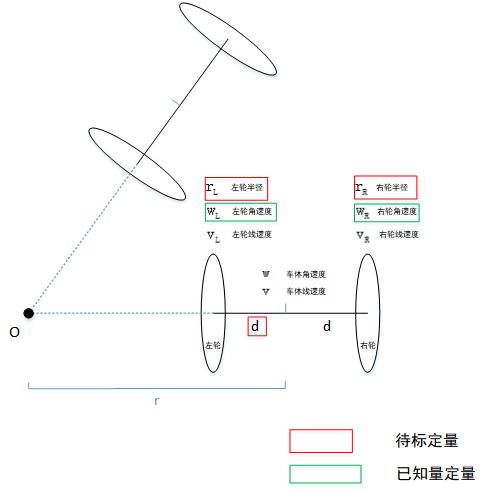
我们要标定的量是轮间距与轮子的半径，建立数学模型的公式目标方向就是用轮间距与轮半径去表示车体的角速度与线速度

如下图所示：

底盘中心相对于车体旋转中心转动的角速度,与两轮相对于车体旋转中心转动的角速度,是相等的。即

通过线速度与角速度关系，引入d

整理得到r

运动解算 求解w
将r带回，可以求得w为：

运动解算 求解v
通过w*r化简即可求得v为：

用轮子的角速度去表示车中心的线速度和角速度即

至此已经通过运动学模型建立的轮速里程计的角速度与车体的线速度、角速度的数学模型

在有了通过轮速里程计计算的车体角速度及线速度后，那么剩下的就需要和激光雷达的数据建立关系。
激光雷达通过匹配，可以知道相对帧之间的平移和旋转。那么通过对车体的角速度及线速度积分即为旋转和平移
需要注意的一点就是轮速里程计更新的频率高，那么就要积分激光雷达帧间所有里程计的数据
里程计在一次更新内进行匀速假设。

角速度积分关系如下

线速度积分关系如下

在实际中需要进行离散化

上式写成矩阵形式，方便使用最小二乘

上面是通过第i帧激光与其帧间的轮速里程计累加建立的数学方程。
那么m帧激光雷达数据和对应的轮速里程计数据建立的线性方程组即为如下形式：

这里即有了线性最小二乘的形式


至此即可求出J21和J22
之后通过平移关系，求解出D后，即可完成标定。

对于轮速里程计通过积分求解平移公式如下：

同样，在实际中需要进行离散化

上面的离散方程里D是待标定参数，J21和J22是上面已求出的，角速度和角度是可以计算得到的，所以D后面括号里的一大坨为已知量

与激光雷达的平移建立联系，可得下面方程租

这里又建立了线性最小二乘方程组，即可求出D
目前已知Ｄ、J21、J22

Code

首先通过采集及处理数据 得到

• 轮速里程计的信息 t_r(该段持续时间) w_L(该段左轮角速度) w_R(该段右轮角速度)
• 激光雷达的时间和匹配值 t_s(该段持续时间) s_x (x位移) s_y(y位移) s_th(角度)

int main(int argc, char** argv)
{
    // 放置激光雷达的时间和匹配值 t_s s_x s_y s_th
    vector<vector<double>> s_data;
    // 放置轮速计的时间和左右轮角速度 t_r w_L w_R
    vector<vector<double>> r_data;

    //通过 ifstream 读取txt文件
    ifstream fin_s(scan_match_file);
    ifstream fin_r(odom_file);

    //判断文件路径是否正确
    if (!fin_s || !fin_r)
    {
        cerr << "文件路径设置有问题" << endl;
        return 1;
    }

    // 读取激光雷达的匹配值
    //eof()判断是否读完
    while (!fin_s.eof()) {
        double s_t, s_x, s_y, s_th;
        fin_s >> s_t >> s_x >> s_y >> s_th;
        s_data.push_back(vector<double>({s_t, s_x, s_y, s_th}));
    }
    fin_s.close();

    // 读取两个轮子的角速度
    while (!fin_r.eof()) {
        double t_r, w_L, w_R;
        fin_r >> t_r >> w_L >> w_R;
        r_data.push_back(vector<double>({t_r, w_L, w_R}));
    }
    fin_r.close();

通过 ifstream 读取txt中的数据,并赋值给最前面声明的两个数据

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++

    //计算中间变量J_21和J_22
    Eigen::MatrixXd A;//声明线性最小二乘的矩阵A
    Eigen::VectorXd b;//声明线性最小二乘的矩阵B
    // 设置数据长度
    A.conservativeResize(5000, 2);//设置A的大小 5000*2
    b.conservativeResize(5000);//设置B的大小 5000*1
    A.setZero();//A矩阵清零
    b.setZero();//B矩阵清零

    size_t id_r = 0;//轮速里程计数据取值id
    size_t id_s = 0;//激光数据取值id
    double last_rt = r_data[0][0];//取出轮速里程计第一个数据的时间
    double w_Lt = 0;//里程计角度积分累加值
    double w_Rt = 0;
    while (id_s < 5000)
    {
        // 激光的匹配信息
        const double &s_t = s_data[id_s][0];//该组激光雷达的时间
        const double &s_th = s_data[id_s][3];//该组激光雷达的角度
        // 里程计信息
        const double &r_t = r_data[id_r][0];//该组里程计的时间
        const double &w_L = r_data[id_r][1];//该组里程计的左轮角速度
        const double &w_R = r_data[id_r][2];//该组里程计的右轮角速度

        //由于里程计更新的频率高,则选择里程计的时间刚大于激光雷达的时间的时候为匹配对
        ++id_r;//里程计的取值id加1

        // 在2帧激光匹配时间内进行里程计角度积分
        if (r_t < s_t)//如果轮速里程计的时间小于激光雷达的时间 则时间未匹配好
        {
            double dt = r_t - last_rt;//轮速里程计 该段数据的 dt
            w_Lt += w_L * dt;//累加该段的角速度
            w_Rt += w_R * dt;//累加该段的角速度
            last_rt = r_t;//更新时间
        }
        else//时间匹配上了
        {
            double dt = s_t - last_rt;//轮速里程计 该段数据的 dt
            w_Lt += w_L * dt;//累加该段的角速度
            w_Rt += w_R * dt;//累加该段的角速度
            last_rt = s_t;//更新时间
            // 填充A, b矩阵
            A(id_s, 0) = w_Lt;//填充A
            A(id_s, 1) = w_Rt;//填充A
            b[id_s] = s_th;//填充B
            w_Lt = 0;//清零一次激光雷达对应的 里程计角度值
            w_Rt = 0;//清零一次激光雷达对应的 里程计角度值
            ++id_s;//处理下一个激光雷达数据
        }
    }

首先用读入的数据填充A矩阵和B矩阵
上面每一行代码均已注释
注意:
和推导不同的是,轮速里程计的更新频率快,所以需要找到时间最为接近的数据作为填入值.
那么在一次的激光雷达更新,则里程计已更新多次,那么需要累加这几次的角度,即出现了
w_Lt += w_L * dt;//累加该段的角速度
w_Rt += w_R * dt;//累加该段的角速度

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

    // 进行最小二乘求解
    Eigen::Vector2d J21J22;
    J21J22 = A.bdcSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b);
    const double &J21 = J21J22(0);
    const double &J22 = J21J22(1);
    cout << "J21: " << J21 << endl;
    cout << "J22: " << J22 << endl;

通过最小二乘,求解 J21和J22
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

    // 求解轮间距b
    Eigen::VectorXd C;//声明线性最小二乘的矩阵A
    Eigen::VectorXd S;//声明线性最小二乘的矩阵b
    // 设置数据长度
    C.conservativeResize(10000);//5000个数据,需要5000*2的长度
    S.conservativeResize(10000);//5000个数据,需要5000*2的长度
    C.setZero();//A矩阵清零
    S.setZero();//b矩阵清零

    id_r = 0;//轮速里程计数据取值id
    id_s = 0;//激光雷达数据取值id
    last_rt = r_data[0][0];//取出轮速里程计第一个数据的时间
    double th = 0;//累加的轮速里程计 角度
    double cx = 0;//累加的轮速里程计 x
    double cy = 0;//累加的轮速里程计 y
    while (id_s < 5000)
    {
        // 激光的匹配信息
        const double &s_t = s_data[id_s][0];//该组激光雷达的时间
        const double &s_x = s_data[id_s][1];//该组激光雷达的x
        const double &s_y = s_data[id_s][2];//该组激光雷达的y
        // 里程计信息
        const double &r_t = r_data[id_r][0];//该组里程计的时间
        const double &w_L = r_data[id_r][1];//该组里程计的左轮角速度
        const double &w_R = r_data[id_r][2];//该组里程计的右轮角速度
        ++id_r;//里程计的取值id加1
        // 在2帧激光匹配时间内进行里程计位置积分
        if (r_t < s_t)//如果轮速里程计的时间小于激光雷达的时间 则时间未匹配好
        {
            double dt = r_t - last_rt;
            cx += 0.5 * (-J21 * w_L * dt + J22 * w_R * dt) * cos(th);//累加里程计该段时间的x
            cy += 0.5 * (-J21 * w_L * dt + J22 * w_R * dt) * sin(th);//累加里程计该段时间的y
            th += (J21 * w_L + J22 * w_R) * dt;//累加里程计该段时间的角度
            last_rt = r_t;//更新时间
        }
        else//时间匹配了
        {
            double dt = s_t - last_rt;
            cx += 0.5 * (-J21 * w_L * dt + J22 * w_R * dt) * cos(th);//累加里程计该段时间的x
            cy += 0.5 * (-J21 * w_L * dt + J22 * w_R * dt) * sin(th);//累加里程计该段时间的y
            th += (J21 * w_L + J22 * w_R) * dt;//累加里程计该段时间的角度
            last_rt = s_t;//更新时间
            // 填充C, S矩阵
            //TODO: (4~5 lines)
            C[id_s * 2] = cx;//填充A
            C[id_s * 2 + 1] = cy;//填充A
            S[id_s * 2] = s_x;//填充b
            S[id_s * 2 + 1] = s_y;//填充b
            //end of TODO
            cx = 0;//清零一次激光雷达对应的 里程计x
            cy = 0;//清零一次激光雷达对应的 里程计y
            th = 0;//清零一次激光雷达对应的 里程计角度
            ++id_s;//处理下一次激光雷达数据
        }
    }

和上面求J21和J22的时填充A和b类似.
每行已做注释
值得注意的就是需要积分激光雷达两帧时间段内的里程计的多次数据
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

    // 进行最小二乘求解，计算b, r_L, r_R
    double b_wheel;//轮间距
    double r_L;//左轮半径
    double r_R;//右轮半径
    
    b_wheel = C.colPivHouseholderQr().solve(S)[0];
    r_L = -J21 * b_wheel;
    r_R = J22 * b_wheel;
    
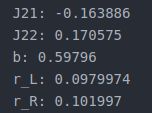
    cout << "b: " << b_wheel << endl;
    cout << "r_L: " << r_L << endl;
    cout << "r_R: " << r_R << endl;

    return 0;

进行最小二乘求解，计算b, r_L, r_R
完毕
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Result

一个数据标定结果如下: