数据结构(C语言版)——二叉树的顺序存储结构(代码版)
一、代码
#include 二、代码中重要的函数或语句
(一)、
typedef struct biTree{
char data[MAXSIZE];
}BITREE,*BITREEPOINTER;
上面定义了一个用于存取二叉树顺序结构的数组
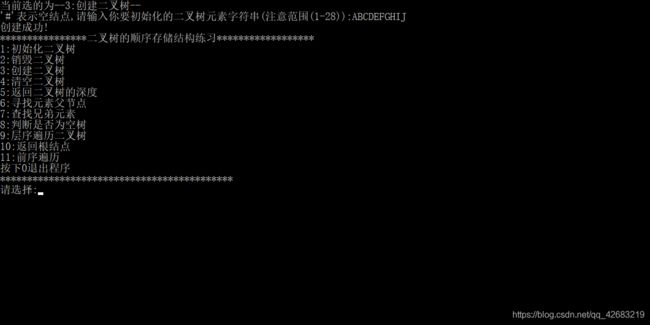
(二)、创建二叉树
char getChar[SIZE];
int inputLength,i;
printf("'#'表示空结点,请输入你要初始化的二叉树元素字符串(注意范围(1-%d)):",SIZE-2);
fflush(stdin);//清除缓冲区的换行符
fgets(getChar,SIZE,stdin);
if(getChar[strlen(getChar)-1]!='\n')
{//判断是否超过范围
printf("输入超过范围!\n");
fflush(stdin);
return ERROR;
}
getChar[strlen(getChar)-1]='\0'; //如果没有超过范围,去掉其中的换行符
inputLength=strlen(getChar);
(*T)->data[0]=inputLength;//存储二叉树链表的元素个数
for(i=1;i<=inputLength;i++)
{
(*T)->data[i]=getChar[i-1];
}
fflush(stdin);//清除缓冲区
printf("创建成功!\n");
在创建二叉树的时候,要注意fgets函数的特性,它会在输入一行结束后加上\n\0,在一个超过范围的输入时它会在一行中加入\0不加\n,所以你可以通过该特性判断输入的元素是否超过范围。
(*T)->data[0]在0的位置存入的是输入字符串的大小
(三)、返回二叉树的深度
int depth;
depthPre=log10((*T)->data[0])/log10(2);
depth=(int)ceil(depthPre);
在计算二叉树深度的时候,选用了log函数进行计算。计算的结果再向上取整,最后转换为int类型。因为二叉树的特殊性,在0号位置存储着二叉树元素的最大值。所以计算树的深度就可以log2((*T)->data[0])来计算。
注:#符号代表空元素(空树)
三、运行截图
①:初始化下图的二叉树,并返回根节点
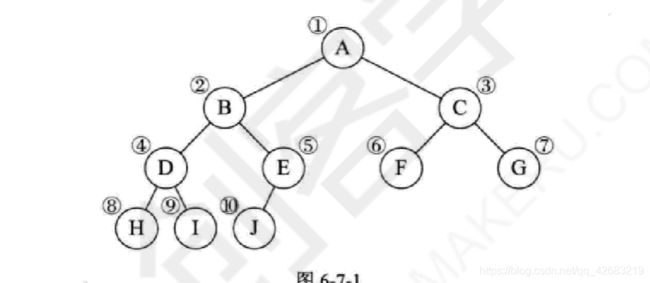
根节点为

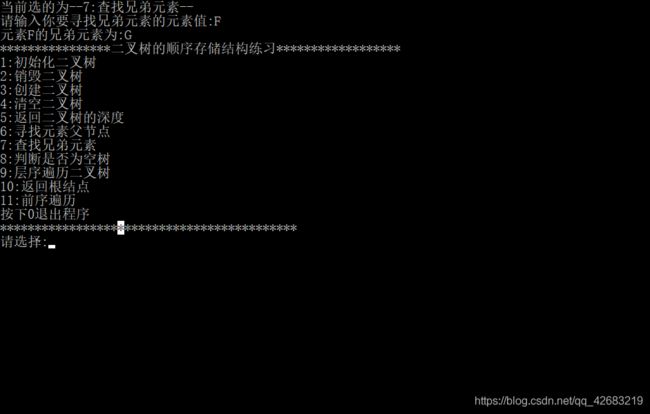
②:查看树的深度以后兄弟结点
如有错误欢迎指出