TensorFlow 手写实现卷积神经网络CNN
目录
一:卷积神经网络基础概念
二:MNIST数据集
三:卷积神经网络搭建过程
一:卷积神经网络基础概念
普通的深层神经网络,层与层之间通过全连接进行稠密矩阵运算,矩阵中的权重系数比较多(参数多),影响效率且容易出现过拟合
卷积神经网络的结构:卷积层、激活函数、池化层、全连接层
卷积层:将原始图片通过Filter(过滤器,权重矩阵,卷积核,观察窗口),分割出局部信息,过滤器经过多次平移取样(步长)形成一个个局部信息然后组成卷积层,卷积层中的每一个单位点对应前面层的局部信息;(卷积的意义:一个点与临近的点联系比较紧密,离得越远的点,联系越不紧密)当神经网络中的层数逐渐增加时,卷积层中的局部信息就会逐渐与全局信息产生联系;
过滤器大小一般设为3*3或5*5(奇数),步长1
(卷积核的计算过程:卷积核(权重矩阵)与输入图片的局部矩阵中的像素进行一一对应的线性相乘求和再加偏置得到卷积层中的一个单位值,卷积核进行平移继续得到卷积层中的全部值(2维)
可以有多个卷积核,多个卷积核的观察(计算)结果共同组成卷积层(3维)。如果图片是3通道,那么卷积核也是3通道,3个通道的计算结果再求和 加偏置形成卷积层中的单位点(卷积层形状的深度与通道数无关,只与卷积核的数量有关))
池化层:(下采样、欠采样,特征降维),减少矩阵的长和宽(也是通过观察窗口的形式实现),减少参数个数,避免过拟合。分为最大池化层和平均池化层(将观察窗口中的最大值或平均值作为其输出)
池化层中的观察窗口大小一般设为2*2,步长2
(池化层的计算过程:通过观察窗口截取卷积层,截取出的矩阵中的最大值(或平均值)作为池化层中的单位点,观察窗口进行平移形成整个池化层。池化只会减少卷积层形状的长和宽,并不会影响形状的深度)
激活函数:解决非线性划分问题,一般是一个非线性的函数,(神经网络的矩阵运算只是一个线性变化)
全连接层:前面的卷积和池化相当于做特征工程(并没有进行矩阵乘法,只是一一对应的线性相乘),后面的全连接相当于做真正的特征加权(矩阵乘法)
最后的全连接层在整个卷积神经网络中起到“分类器”的作用(如果卷积神经网络不是用于分类问题,那么可以不使用全连接层)
为什么要用Relu激活函数,而不用sigmoid激活函数?
第一,采用sigmoid激活函数,反向传播求误差梯度时,计算量相对大,而采用Relu激活函数,整个过程的计算量节省很多
第二,对于深层网络,sigmoid函数反向传播时,很容易就会出现梯度消失(梯度爆炸)的情况(求不出权重和偏置)
二:MNIST数据集
获取地址如下,下载下来即可
http://yann.lecun.com/exdb/mnist/
三:卷积神经网络搭建过程
1 准备输入数据的占位符
# 网络搭建
# 特征标签占位符
# 图片大小28*28=784
xs = tf.placeholder(tf.float32, shape=[None, input_size])
# 目标类别:10个类别。 one-hot编码形式表示
ys = tf.placeholder(tf.float32, shape=[None, num_class])
# -1任意张图片 size(28*28) 1深度
# 对x进行形状的改变(变成4阶张量) [None, 784]--->[None, 28, 28, 1]
x_image = tf.reshape(xs, [-1, 28, 28, 1])2 图片数据-》卷积层-》激活函数-》池化层
# CNN构建
# 图片数据-->卷积层-->激活函数-->池化层
# 第一层卷积层 卷积核5*5
# 随机初始化卷积核的矩阵权重 卷积核大小:5*5*1(1个通道,与输入图片通道数一致) 32个卷积核(决定卷积后形状的深度)
w_conv1 = tf.Variable(tf.random_normal(shape=[5, 5, 1, 32], stddev=0.01))
# 初始化偏置
b_conv1 = tf.Variable(tf.constant(0.01, shape=[32]))
# 卷积层
# 卷积、激活函数 输入的张量x_reshape必须四阶 [None, 28, 28, 1]---> [None, 28, 28, 32]
# padding="SAME"表示进行零填充,让卷积层的宽高与图片宽高一致(填充的围数自动计算,卷积核尺寸是奇数好计算)
# strides:卷积步长 上右下左 保证与原图像大小一致
conv1 = tf.nn.conv2d(x_image, w_conv1, strides=[1, 1, 1, 1], padding='SAME')
# 激活层
h_conv1 = tf.nn.relu(conv1 + b_conv1)
# 池化 窗口大小:2*2;步长:2 [None, 28, 28, 32]--->[None, 14, 14, 32] 池化只会改变形状的宽高,不会改变深度
h_pool1 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')3 再次卷积 深层神经网络
# 再次卷积(深层神经网络) 卷积层-->激活函数-->池化层
# 随机初始化卷积核的矩阵权重 卷积核大小:5*5*32 64个卷积核
w_conv2 = tf.Variable(tf.random_normal(shape=[5, 5, 32, 64], stddev=0.01))
# 初始化偏置 64个偏置
b_conv2 = tf.Variable(tf.constant(0.01, shape=[64]))
# 卷积、激活函数 [None, 14, 14, 32]---> [None, 14, 14, 64] padding="SAME":卷积只会改变形状的深度,不会改变宽高
conv2 = tf.nn.conv2d(h_pool1, w_conv2, strides=[1, 1, 1, 1], padding='SAME')
# 激活层 14*14*64
h_conv2 = tf.nn.relu(conv2 + b_conv2)
# 池化 窗口大小:2*2;步长:2 [None, 14, 14, 64]--->[None, 7, 7, 64] 池化只会改变形状的宽高,不会改变深度。
h_pool2 = tf.nn.max_pool(h_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')4 全连接层
# 全连接层 矩阵乘法:[None, 7, 7, 64]--->[None, 7*7*64]*[7*7*64, 10] + [10] = [None, 10] (目标类别数10,one-hot编码)
# 随机初始化全连接的权重矩阵 目标类别数
w_fc1 = tf.Variable(tf.random_normal(shape=[7 * 7 * 64, 1024]))
# 初始化偏置
b_fc1 = tf.Variable(tf.constant(0.01, shape=[1024]))
# 输出的是矩阵 行不需要 列7*7*64 -1任意行
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
# wx+b
h_fc1 = tf.matmul(h_pool2_flat, w_fc1) + b_fc1
# 激活
h_fc1 = tf.nn.relu(h_fc1)
# 全连层2 分类 看作输出层 返回每一种情况的概率
w_fc2 = tf.Variable(tf.random_normal(shape=[1024, num_class]))
b_fc2 = tf.Variable(tf.constant(0.01, shape=[num_class]))
h_fc2 = tf.matmul(h_fc1, w_fc2) + b_fc2
# 进行矩阵运算得出每个样本的10个目标类别结果(可以通过softmax函数转换成10个目标类别的概率,最大的概率即为预测类别)
y_predict = tf.nn.softmax(h_fc2)5 交叉熵损失计算
# 卷积神经网络模型定义结束
# 进行交叉熵损失计算
# 求出所有样本的交叉熵损失,然后tf.reduce_mean()计算平均值
# 构建损失函数
# 求平均交叉熵损失 y_predict是没有经过softmax函数处理的预测结果
loss = tf.reduce_mean(-tf.reduce_mean(ys * tf.log(y_predict), reduction_indices=[1]))
# 优化器 梯度下降优化损失
# 0.0001表示学习率 (学习率并不是一个超参数)(深层神经网络的学习率一般设很小)
Optimizer = tf.train.AdamOptimizer(0.0001).minimize(loss)6 开启会话 迭代训练
# 定义一个初始化变量的op
init = tf.global_variables_initializer()
# 创建会话
with tf.Session() as sess:
# 初始化变量
sess.run(init)
# 迭代训练,更新参数 (迭代1000次)
for i in range(1000):
# 取出训练集的特征值和目标值 (每次迭代取出100个样本)
batch_x, batch_y = mnist_data.train.next_batch(100)
# 运行Optimizer训练优化 (feed_dict:用实时的训练数据填充占位符)
sess.run(Optimizer, feed_dict={xs: batch_x, ys: batch_y})
# train_loss = sess.run(loss, feed_dict={xs: batch_x, ys: batch_y})
# print(train_loss)
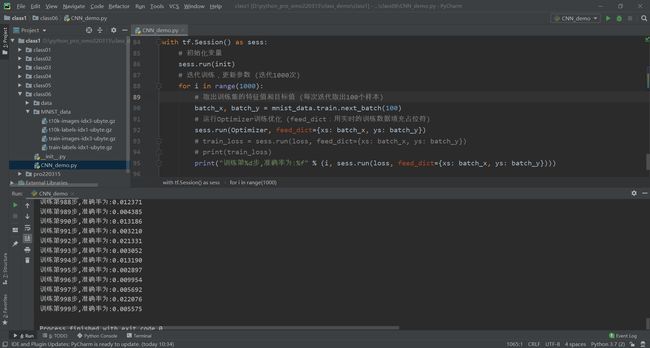
print("训练第%d步,准确率为:%f" % (i, sess.run(loss, feed_dict={xs: batch_x, ys: batch_y})))测试如下,准确率在0.005左右
完整源码分享
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 读取数据
# TensorFlow自带的数据集(手写数字图片,55000个训练样本,10000个测试样本,图片尺寸28*28=784)
mnist_data = input_data.read_data_sets("MNIST_data/", one_hot=True)
# print(mnist_data, type(mnist_data))
input_size = 28 * 28
num_class = 10
# 网络搭建
# 特征标签占位符
# 图片大小28*28=784
xs = tf.placeholder(tf.float32, shape=[None, input_size])
# 目标类别:10个类别。 one-hot编码形式表示
ys = tf.placeholder(tf.float32, shape=[None, num_class])
# -1任意张图片 size(28*28) 1深度
# 对x进行形状的改变(变成4阶张量) [None, 784]--->[None, 28, 28, 1]
x_image = tf.reshape(xs, [-1, 28, 28, 1])
# CNN构建
# 图片数据-->卷积层-->激活函数-->池化层
# 第一层卷积层 卷积核5*5
# 随机初始化卷积核的矩阵权重 卷积核大小:5*5*1(1个通道,与输入图片通道数一致) 32个卷积核(决定卷积后形状的深度)
w_conv1 = tf.Variable(tf.random_normal(shape=[5, 5, 1, 32], stddev=0.01))
# 初始化偏置
b_conv1 = tf.Variable(tf.constant(0.01, shape=[32]))
# 卷积层
# 卷积、激活函数 输入的张量x_reshape必须四阶 [None, 28, 28, 1]---> [None, 28, 28, 32]
# padding="SAME"表示进行零填充,让卷积层的宽高与图片宽高一致(填充的围数自动计算,卷积核尺寸是奇数好计算)
# strides:卷积步长 上右下左 保证与原图像大小一致
conv1 = tf.nn.conv2d(x_image, w_conv1, strides=[1, 1, 1, 1], padding='SAME')
# 激活层
h_conv1 = tf.nn.relu(conv1 + b_conv1)
# 池化 窗口大小:2*2;步长:2 [None, 28, 28, 32]--->[None, 14, 14, 32] 池化只会改变形状的宽高,不会改变深度
h_pool1 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# 再次卷积(深层神经网络) 卷积层-->激活函数-->池化层
# 随机初始化卷积核的矩阵权重 卷积核大小:5*5*32 64个卷积核
w_conv2 = tf.Variable(tf.random_normal(shape=[5, 5, 32, 64], stddev=0.01))
# 初始化偏置 64个偏置
b_conv2 = tf.Variable(tf.constant(0.01, shape=[64]))
# 卷积、激活函数 [None, 14, 14, 32]---> [None, 14, 14, 64] padding="SAME":卷积只会改变形状的深度,不会改变宽高
conv2 = tf.nn.conv2d(h_pool1, w_conv2, strides=[1, 1, 1, 1], padding='SAME')
# 激活层 14*14*64
h_conv2 = tf.nn.relu(conv2 + b_conv2)
# 池化 窗口大小:2*2;步长:2 [None, 14, 14, 64]--->[None, 7, 7, 64] 池化只会改变形状的宽高,不会改变深度。
h_pool2 = tf.nn.max_pool(h_conv2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# 全连接层 矩阵乘法:[None, 7, 7, 64]--->[None, 7*7*64]*[7*7*64, 10] + [10] = [None, 10] (目标类别数10,one-hot编码)
# 随机初始化全连接的权重矩阵 目标类别数
w_fc1 = tf.Variable(tf.random_normal(shape=[7 * 7 * 64, 1024]))
# 初始化偏置
b_fc1 = tf.Variable(tf.constant(0.01, shape=[1024]))
# 输出的是矩阵 行不需要 列7*7*64 -1任意行
h_pool2_flat = tf.reshape(h_pool2, [-1, 7 * 7 * 64])
# wx+b
h_fc1 = tf.matmul(h_pool2_flat, w_fc1) + b_fc1
# 激活
h_fc1 = tf.nn.relu(h_fc1)
# 全连层2 分类 看作输出层 返回每一种情况的概率
w_fc2 = tf.Variable(tf.random_normal(shape=[1024, num_class]))
b_fc2 = tf.Variable(tf.constant(0.01, shape=[num_class]))
h_fc2 = tf.matmul(h_fc1, w_fc2) + b_fc2
# 进行矩阵运算得出每个样本的10个目标类别结果(可以通过softmax函数转换成10个目标类别的概率,最大的概率即为预测类别)
y_predict = tf.nn.softmax(h_fc2)
# 卷积神经网络模型定义结束
# 进行交叉熵损失计算
# 求出所有样本的交叉熵损失,然后tf.reduce_mean()计算平均值
# 构建损失函数
# 求平均交叉熵损失 y_predict是没有经过softmax函数处理的预测结果
loss = tf.reduce_mean(-tf.reduce_mean(ys * tf.log(y_predict), reduction_indices=[1]))
# 优化器 梯度下降优化损失
# 0.0001表示学习率 (学习率并不是一个超参数)(深层神经网络的学习率一般设很小)
Optimizer = tf.train.AdamOptimizer(0.0001).minimize(loss)
# 定义一个初始化变量的op
init = tf.global_variables_initializer()
# 创建会话
with tf.Session() as sess:
# 初始化变量
sess.run(init)
# 迭代训练,更新参数 (迭代1000次)
for i in range(1000):
# 取出训练集的特征值和目标值 (每次迭代取出100个样本)
batch_x, batch_y = mnist_data.train.next_batch(100)
# 运行Optimizer训练优化 (feed_dict:用实时的训练数据填充占位符)
sess.run(Optimizer, feed_dict={xs: batch_x, ys: batch_y})
# train_loss = sess.run(loss, feed_dict={xs: batch_x, ys: batch_y})
# print(train_loss)
print("训练第%d步,准确率为:%f" % (i, sess.run(loss, feed_dict={xs: batch_x, ys: batch_y})))