PyTorch学习笔记-6.PyTorch的正则化

6.PyTorch的正则化

6.1.正则项

为了减小过拟合，通常可以添加正则项，常见的正则项有L1正则项和L2正则项

L1正则化目标函数：

L2正则化目标函数：

PyTorch中添加L2正则：PyTorch的优化器中自带一个参数weight_decay，用于指定权值衰减率，相当于L2正则化中的λ参数。

权值未衰减的更新公式：

权值衰减的更新公式：

下面，分别通过不添加L2正则与添加L2正则进行比较：

代码实现：

# -*- coding:utf-8 -*-
import torch
import numpy as np
import random
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.utils.tensorboard import SummaryWriter

def set_seed(seed=1):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)

set_seed(1)  # 设置随机种子

# 隐藏层神经单元数量
n_hidden = 200
# 迭代次数
max_iter = 2000
# 每200轮进行一次绘图
disp_interval = 200
# 学习率
lr_init = 0.01

# 1.准备数据
def get_data(num_data=10, x_range=(-1, 1)):

    # 定义权重
    w = 1.5
    # 定义训练集的x
    # *x_range表示将参数名为x_range的内容打散，即生成-1到1的10个数并扩展维度
    train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
    # 定义训练集的y，为w*x+正太分布的随机数
    train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
    # 生成测试集
    test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
    test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())

    return train_x, train_y, test_x, test_y

train_x, train_y, test_x, test_y = get_data(x_range=(-1, 1))

# 2.创建模型
class MLP(nn.Module):
    def __init__(self, neural_num):
        super(MLP, self).__init__()
        # 利用容器构建模型
        self.linears = nn.Sequential(
            # 创建线性层和激活函数
            nn.Linear(1, neural_num),
            nn.ReLU(inplace=True),
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),
            nn.Linear(neural_num, 1),
        )

    def forward(self, x):
        return self.linears(x)

# 创建两个模型，第一个不添加L2正则，第二个添加L2正则
net_normal = MLP(neural_num=n_hidden)
net_weight_decay = MLP(neural_num=n_hidden)

# 3.创建优化器
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)

# 4.定义损失函数
loss_func = torch.nn.MSELoss()

# 5.开始训练
# 定义tensorboard的输出路径
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):

    # 分别用两个模型对训练集训练，得到预测结果
    pred_normal, pred_wdecay = net_normal(train_x), net_weight_decay(train_x)
    # 分别获得损失
    loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)

    # 反向传播
    loss_normal.backward()
    loss_wdecay.backward()

    # 执行优化
    optim_normal.step()
    optim_wdecay.step()

    # 清空梯度
    optim_normal.zero_grad()
    optim_wdecay.zero_grad()

    #可视化和绘图
    if (epoch+1) % disp_interval == 0:

        # 可视化
        for name, layer in net_normal.named_parameters():
            # 绘制直方图，分别添加tag，value值，global_step即y轴
            writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
            writer.add_histogram(name + '_data_normal', layer, epoch)

        for name, layer in net_weight_decay.named_parameters():
            writer.add_histogram(name + '_grad_weight_decay', layer.grad, epoch)
            writer.add_histogram(name + '_data_weight_decay', layer, epoch)

        # 利用模型对测试集测试并得到预测结果
        test_pred_normal, test_pred_wdecay = net_normal(test_x), net_weight_decay(test_x)

        # 绘图
        plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
        plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
        plt.plot(test_x.data.numpy(), test_pred_normal.data.numpy(), 'r-', lw=3, label='no weight decay')
        plt.plot(test_x.data.numpy(), test_pred_wdecay.data.numpy(), 'b--', lw=3, label='weight decay')
        plt.text(-0.25, -1.5, 'no weight decay loss={:.6f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
        plt.text(-0.25, -2, 'weight decay loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})

        plt.ylim((-2.5, 2.5))
        plt.legend(loc='upper left')
        plt.title("Epoch: {}".format(epoch+1))
        plt.show()
        plt.close()

 

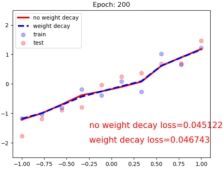
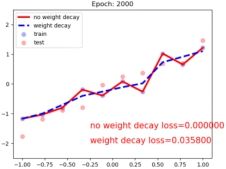
plt绘制图：

 

 

 

可以看出当设置正则后的拟合曲线更平滑，而没有正则的曲线发生了过拟合

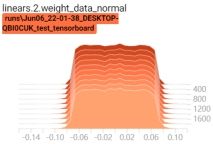
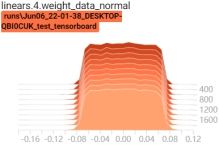
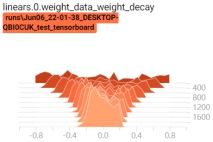
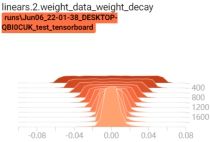
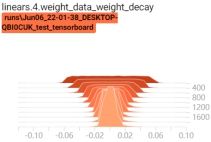
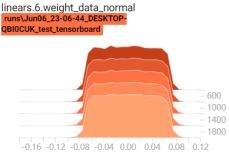
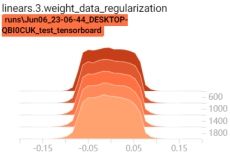
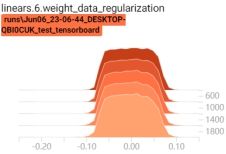
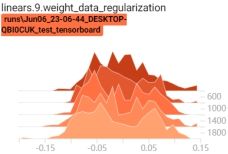
启动tensorboard客户端，查看权重变换过程：tensorboard --logdir=./

 

 

 

可以看到，当有正则项时，权重在不断变小

6.2.Dropout

Dropout：随机失活

指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。注意是暂时，对于随机梯度下降来说，由于是随机丢弃，故而每一个mini-batch都在训练不同的网络。

上图为Dropout的可视化表示，左边是应用Dropout之前的网络，右边是应用了Dropout的同一个网络。

 

PyTorch的Dropout

torch.nn.Dropout

功能：Dropout层

• p：被舍弃概率， 失活概率

torch.nn.Dropout(p=0.5, inplace=False)

实现细节：

Dropout 在训练时采用，是为了减少神经元对部分上层神经元的依赖，减少过拟合的风险。

而在测试时，应该用整个训练好的模型，因此不需要dropout。

因此，训练时权重均乘以 ，即除以，保证结果的尺度不变

测试时，所有权重乘以

代码实现：

# -*- coding:utf-8 -*-
import torch
import numpy as np
import random
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.utils.tensorboard import SummaryWriter

def set_seed(seed=1):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)

set_seed(1)  # 设置随机种子

n_hidden = 200
max_iter = 2000
disp_interval = 400
lr_init = 0.01

# 1.准备数据
def get_data(num_data=10, x_range=(-1, 1)):

    w = 1.5
    train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
    train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
    test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
    test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())

    return train_x, train_y, test_x, test_y

train_x, train_y, test_x, test_y = get_data(x_range=(-1, 1))

# 2.创建模型
class MLP(nn.Module):
    def __init__(self, neural_num, d_prob=0.5):
        super(MLP, self).__init__()
        self.linears = nn.Sequential(

            nn.Linear(1, neural_num),
            nn.ReLU(inplace=True),

            # 从第二层开始添加Dropout
            nn.Dropout(d_prob),
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),

            nn.Dropout(d_prob),
            nn.Linear(neural_num, neural_num),
            nn.ReLU(inplace=True),

            nn.Dropout(d_prob),
            nn.Linear(neural_num, 1),
        )

    def forward(self, x):
        return self.linears(x)

# 创建两个模型，一个不添加Dropout，另一个添加Dropout
net_prob_0 = MLP(neural_num=n_hidden, d_prob=0.)
net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5)

# 3.创建优化器
optim_normal = torch.optim.SGD(net_prob_0.parameters(), lr=lr_init, momentum=0.9)
optim_reglar = torch.optim.SGD(net_prob_05.parameters(), lr=lr_init, momentum=0.9)

# 4.创建损失函数
loss_func = torch.nn.MSELoss()

# 5.开始训练
writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):

    pred_normal, pred_wdecay = net_prob_0(train_x), net_prob_05(train_x)
    loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)

    loss_normal.backward()
    loss_wdecay.backward()

    optim_normal.step()
    optim_reglar.step()

    optim_normal.zero_grad()
    optim_reglar.zero_grad()

    if (epoch+1) % disp_interval == 0:

        # 将模型设置为测试状态，因为测试时不会使用dropout
        net_prob_0.eval()
        net_prob_05.eval()

        # 可视化
        for name, layer in net_prob_0.named_parameters():
            writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
            writer.add_histogram(name + '_data_normal', layer, epoch)

        for name, layer in net_prob_05.named_parameters():
            writer.add_histogram(name + '_grad_regularization', layer.grad, epoch)
            writer.add_histogram(name + '_data_regularization', layer, epoch)

        test_pred_prob_0, test_pred_prob_05 = net_prob_0(test_x), net_prob_05(test_x)

        # 绘图
        plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
        plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
        plt.plot(test_x.data.numpy(), test_pred_prob_0.data.numpy(), 'r-', lw=3, label='d_prob_0')
        plt.plot(test_x.data.numpy(), test_pred_prob_05.data.numpy(), 'b--', lw=3, label='d_prob_05')
        plt.text(-0.25, -1.5, 'd_prob_0 loss={:.8f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
        plt.text(-0.25, -2, 'd_prob_05 loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})

        plt.ylim((-2.5, 2.5))
        plt.legend(loc='upper left')
        plt.title("Epoch: {}".format(epoch+1))
        plt.show()
        plt.close()

        # 将模型设置回训练状态，即添加dropout
        net_prob_0.train()
        net_prob_05.train()

 

plt绘制图：

 

可以看出当设置Dropout后的拟合曲线更平滑，而没有Dropout的曲线发生了过拟合

启动tensorboard客户端，查看权重变换过程：tensorboard --logdir=./

 

 

6.3.Batch Normalization

Batch Normalization：批标准化，batch方向做归一化

批：一批数据，通常为mini-batch
标准化： 0均值， 1方差
计算方式：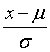

输入： x的一个mini-batch：

可学习的参数：

输出：

计算过程：

mini-batch的均值：

mini-batch的方差：

标准化：    其中为很小的数，防止分母为0

最终的结果：   这一步称为affine transform

其中为缩放因子，是可学习参数，使得模型更灵活，可以由模型判断数据是否需要标准化或者标准化程度。如：，时，

 

PyTorch的Batch Normalization：

PyTorch要实现Batch Normalization，是通过类实现的，PyTorch提供了3个类：

nn.BatchNorm1d
nn.BatchNorm2d
nn.BatchNorm3d

参数：

• num_features：一个样本特征数量（最重要）
• eps：分母修正项，即上面公式的
• momentum：指数加权平均估计当前mean/var，当前mini-batch的mean/var受前一批影响
• affine：是否需要affine transform
• track_running_stats：是训练状态，还是测试状态，训练状态会计算并使用当前批的mean/var，测试状态使用指数加权平均的running_mean和running_var

 

主要属性：

• running_mean：均值
• running_var：方差
• weight： affine transform中的gamma
• bias： affine transform中的beta

 

mean/var计算公式：

running_mean = (1 - momentum) * pre_running_mean + momentum * mean_t
running_var = (1 - momentum) * pre_running_var + momentum * var_t

即当前的mean/var由上一个mini-batch的mean/var和当前批的mean/var共同决定

 

1d/2d/3d的区别：

1d/2d/3d是针对每个特征的维度而言

1d：

即输入大小的形状可以是batch_size×num_features和batch_size×num_features×width都可以。（输入输出相同）

输入Shape：（N, C）或者(N, C, L)

输出Shape：（N, C）或者（N，C，L）

2d：

该期望输入的大小为batch_size×num_features×height×width（输入输出相同）

输入Shape：（N, C，H, W)

输出Shape：（N, C, H, W）

3d：

该期望输入的大小为batch_size×num_features×depth×height×width（输入输出相同）

输入Shape：（N, C, D, H, W）

输出Shape：（N, C, D, H, W）

下面，分别用代码实现nn.BatchNorm1d/2d/3d

代码实现：nn.BatchNorm1d

# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
import numpy as np
import random

def set_seed(seed=1):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)

set_seed(1)  # 设置随机种子

flag = 1
# flag = 0
if flag:

    # 设置批大小
    batch_size = 3
    # 设置每个样本的特征数
    num_features = 5
    # 设置指数加权平均系数
    momentum = 0.3

    # 特征的形状
    features_shape = (1)

    # 构建全是1的特征
    feature_map = torch.ones(features_shape)
    # 在特征前面增加特征数量维度，即5×1
    feature_maps = torch.stack([feature_map*(i+1) for i in range(num_features)], dim=0)
    # 在特征数量前面增加批大小维度，即3×5×1
    feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)
    # 打印数据及其维度
    print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))

    # 创建BatchNorm1d
    bn = nn.BatchNorm1d(num_features=num_features, momentum=momentum, track_running_stats=True)

    # 设置初始均值与方差，因为第一次计算时前面没有均值与方差
    running_mean, running_var = 0, 1

    for i in range(2):
        # 利用BatchNorm1d对数据进行处理
        outputs = bn(feature_maps_bs)

        # 打印第几次迭代以及迭代时的均值、方差
        print("\niteration:{}, running mean: {} ".format(i, bn.running_mean))
        print("iteration:{}, running var:{} ".format(i, bn.running_var))

        # 手动计算第二个特征的均值与方差
        mean_t, var_t = 2, 0

        running_mean = (1 - momentum) * running_mean + momentum * mean_t
        running_var = (1 - momentum) * running_var + momentum * var_t

        print("iteration:{}, 第二个特征的running mean: {} ".format(i, running_mean))
        print("iteration:{}, 第二个特征的running var:{}".format(i, running_var))

input data: tensor([[[1.],          [2.],          ...          [5.]]]) shape is torch.Size([3, 5, 1])   iteration:0, running mean: tensor([0.3000, 0.6000, 0.9000, 1.2000, 1.5000]) iteration:0, running var:tensor([0.7000, 0.7000, 0.7000, 0.7000, 0.7000]) iteration:0, 第二个特征的running mean: 0.6 iteration:0, 第二个特征的running var:0.7   iteration:1, running mean: tensor([0.5100, 1.0200, 1.5300, 2.0400, 2.5500]) iteration:1, running var:tensor([0.4900, 0.4900, 0.4900, 0.4900, 0.4900]) iteration:1, 第二个特征的running mean: 1.02 iteration:1, 第二个特征的running var:0.48999999999999994

 

代码实现：nn.BatchNorm2d

flag = 1
# flag = 0
if flag:

    batch_size = 3
    num_features = 6
    momentum = 0.3

    # 特征维度为2×2
    features_shape = (2, 2)

    feature_map = torch.ones(features_shape)    
    feature_maps = torch.stack([feature_map*(i+1) for i in range(num_features)], dim=0)    
    feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)      

    print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))

    # 创建BatchNorm2d
    bn = nn.BatchNorm2d(num_features=num_features, momentum=momentum)

    running_mean, running_var = 0, 1

    for i in range(2):
        outputs = bn(feature_maps_bs)

# 打印第几次迭代以及迭代时的均值、方差的shape
        print("\niter:{}, running_mean.shape: {}".format(i, bn.running_mean.shape))
        print("iter:{}, running_var.shape: {}".format(i, bn.running_var.shape))

        print("iter:{}, weight.shape: {}".format(i, bn.weight.shape))
        print("iter:{}, bias.shape: {}".format(i, bn.bias.shape))

input data: tensor([[[[1., 1.],           [1., 1.]],            [[2., 2.],           [2., 2.]],            ...          [[6., 6.],           [6., 6.]]]]) shape is torch.Size([3, 6, 2, 2])   iter:0, running_mean.shape: torch.Size([6]) iter:0, running_var.shape: torch.Size([6]) iter:0, weight.shape: torch.Size([6]) iter:0, bias.shape: torch.Size([6])   iter:1, running_mean.shape: torch.Size([6]) iter:1, running_var.shape: torch.Size([6]) iter:1, weight.shape: torch.Size([6]) iter:1, bias.shape: torch.Size([6])

 

代码实现：nn.BatchNorm3d

flag = 1
# flag = 0
if flag:

    batch_size = 3
    num_features = 4
    momentum = 0.3

    # 特征维度为2×2×3
    features_shape = (2, 2, 3)

    feature = torch.ones(features_shape)                            
    feature_map = torch.stack([feature * (i + 1) for i in range(num_features)], dim=0)  
    feature_maps = torch.stack([feature_map for i in range(batch_size)], dim=0)        

    print("input data:\n{} shape is {}".format(feature_maps, feature_maps.shape))

    # 创建BatchNorm3d
    bn = nn.BatchNorm3d(num_features=num_features, momentum=momentum)

    running_mean, running_var = 0, 1

    for i in range(2):
        outputs = bn(feature_maps)

        print("\niter:{}, running_mean.shape: {}".format(i, bn.running_mean.shape))
        print("iter:{}, running_var.shape: {}".format(i, bn.running_var.shape))

        print("iter:{}, weight.shape: {}".format(i, bn.weight.shape))
        print("iter:{}, bias.shape: {}".format(i, bn.bias.shape))

input data: tensor([[[[[1., 1., 1.],            [1., 1., 1.]],             [[1., 1., 1.],            [1., 1., 1.]]],             ...           [[4., 4., 4.],            [4., 4., 4.]]]]]) shape is torch.Size([3, 4, 2, 2, 3])   iter:0, running_mean.shape: torch.Size([4]) iter:0, running_var.shape: torch.Size([4]) iter:0, weight.shape: torch.Size([4]) iter:0, bias.shape: torch.Size([4])   iter:1, running_mean.shape: torch.Size([4]) iter:1, running_var.shape: torch.Size([4]) iter:1, weight.shape: torch.Size([4]) iter:1, bias.shape: torch.Size([4])

 

6.4.常见Normalization

常见的Normalization有：

1. Batch Normalization（ BN）

2. Layer Normalization（ LN）
3. Instance Normalization（ IN）

4. Group Normalization（ GN）

它们的共同点是计算方式相同，都是：

        

不同点是：均值和方差求取方式不同。

 

1. Layer Normalization
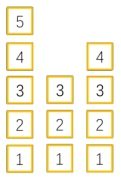
起因： BN不适用于变长的网络，如RNN
思路： channel方向做归一化，逐层计算均值和方差

注意事项：
不再有running_mean和running_var
gamma和beta为逐元素的

变长的网络如下：

nn.LayerNorm
主要参数：
• normalized_shape：该层特征形状
• eps：分母修正项
• elementwise_affine：是否需要affine transform

nn.LayerNorm(normalized_shape, eps=1e-05,
elementwise_affine=True)

 

代码实现：

# -*- coding: utf-8 -*-
import torch
import numpy as np
import random
import torch.nn as nn

def set_seed(seed=1):
    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)

set_seed(1)  # 设置随机种子

flag = 1
# flag = 0
if flag:
    # 批大小
    batch_size = 8
    # 特征数
    num_features = 6

    # 每个特征的shape
    features_shape = (3, 4)

    # 构建数据，最终为B * C * H * W
    feature_map = torch.ones(features_shape)
    feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)
    feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)

    # 输入特征为C * H * W，去掉了B
    ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)  #False
    # 或者从后向前指定维度作为特征设置，注意指定时必须从后向前匹配
    # ln = nn.LayerNorm([3, 4])

    output = ln(feature_maps_bs)

    # 打印权重的shape、输入、输出
    print("Layer Normalization")
    print(ln.weight.shape)
    print(feature_maps_bs[0, ...])
    print(output[0, ...])

Layer Normalization torch.Size([6, 3, 4]) tensor([[[1., 1., 1., 1.],          [1., 1., 1., 1.],          [1., 1., 1., 1.]],           ...         [[6., 6., 6., 6.],          [6., 6., 6., 6.],          [6., 6., 6., 6.]]]) tensor([[[-1.4638, -1.4638, -1.4638, -1.4638],          [-1.4638, -1.4638, -1.4638, -1.4638],          [-1.4638, -1.4638, -1.4638, -1.4638]],           [[-0.8783, -0.8783, -0.8783, -0.8783],          [-0.8783, -0.8783, -0.8783, -0.8783],          [-0.8783, -0.8783, -0.8783, -0.8783]],           ...         [[ 1.4638,  1.4638,  1.4638,  1.4638],          [ 1.4638,  1.4638,  1.4638,  1.4638],          [ 1.4638,  1.4638,  1.4638,  1.4638]]], grad_fn=)

 

注意：这里计算时是按照一层的输入特征所以值进行标准化

 

2. Instance Normalization
起因： BN在图像生成（ Image Generation）中不适用
思路： 一个channel内做归一化，逐Instance（ channel） 计算均值和方差

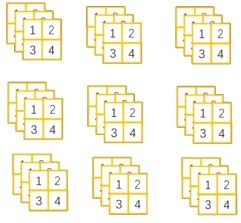
例如：对于下图，在生成图像时，每张图片的风格不同，不能对多个图像进行标准化。

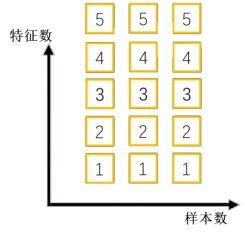
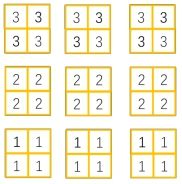
Instance Normalization会在每个样本的每个通道进行标准化，如下面数据中，对其中每个田字格数据分别进行标准化

nn.InstanceNorm
主要参数：
• num_features：一个样本特征数量（最重要）
• eps：分母修正项
• momentum：指数加权平均估计当前mean/var
• affine：是否需要affine transform
• track_running_stats：是训练状态，还是测试状态

nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1,
affine=False, track_running_stats=False)

 

代码实现：

flag = 1
# flag = 0
if flag:

    batch_size = 3
    num_features = 3
    momentum = 0.3

    features_shape = (2, 2)

    feature_map = torch.ones(features_shape)
    feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)
    feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)

    print("Instance Normalization")
    print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))

    instance_n = nn.InstanceNorm2d(num_features=num_features, momentum=momentum)

    outputs = instance_n(feature_maps_bs)

    print(outputs)
    print("\niter:{}, running_mean.shape: {}".format(i, instance_n.running_mean))

Instance Normalization input data: tensor([[[[1., 1.],           [1., 1.]],            ...          [[3., 3.],           [3., 3.]]]]) shape is torch.Size([3, 3, 2, 2]) tensor([[[[0., 0.],           [0., 0.]],            [[0., 0.],           [0., 0.]],           ...          [[0., 0.],           [0., 0.]]]])

 

由于主通道计算，也就是标准化时是按照一个features_shape的大小进行标准化，由于每个features_shape中的数据都是相同的，因此最终输出都是0。

 

3. Group Normalization
起因：小batch样本中， BN估计的值不准
思路：将channel方向分group，然后每个group内做归一化
注意事项：
不再有running_mean和running_var
gamma和beta为逐通道（ channel）的
应用场景：大模型（小batch size）任务

细节：

Group Normalization介于Instance Normalization和Layer Normalization之间，其首先将channel分为许多组（group），对每一组做归一化，BN会受到batchsize大小的影响。如果batchsize太小，算出的均值和方差就会不准确，如果太大，显存又可能不够用。GN算的是channel方向每个group的均值和方差，和batchsize没关系，自然就不受batchsize大小的约束。随着batchsize的减小，GN的表现基本不受影响，而BN的性能却越来越差。

 

如下面数据中，Group Normalization对每个样本特征进行分组，如分为两组，然后再按组进行标准化

 

nn.GroupNorm
主要参数：
• num_groups：分组数，通常设置为2,4,8,16...
• num_channels：通道数（特征数）
• eps：分母修正项
• affine：是否需要affine transform

nn.GroupNorm(num_groups, num_channels,
eps=1e-05, affine=True)

 

代码实现：

flag = 1
# flag = 0
if flag:

    batch_size = 2
    num_features = 4
    # 分组数，注意分组数要能被num_features整除
    num_groups = 2   # 3

    features_shape = (2, 2)

    feature_map = torch.ones(features_shape)
    feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)
    feature_maps_bs = torch.stack([feature_maps * (i + 1) for i in range(batch_size)], dim=0)

    gn = nn.GroupNorm(num_groups, num_features)
    outputs = gn(feature_maps_bs)

    print("Group Normalization")
    # 打印权重，由于gamma和beta为逐通道（ channel）的，所以大小与num_features数量一致
    print(gn.weight.shape)
    print(feature_maps_bs[0])
    print(outputs[0])

Group Normalization torch.Size([4]) tensor([[[1., 1.],          [1., 1.]],           [[2., 2.],          [2., 2.]],           [[3., 3.],          [3., 3.]],           [[4., 4.],          [4., 4.]]]) tensor([[[-1.0000, -1.0000],          [-1.0000, -1.0000]],           [[ 1.0000,  1.0000],          [ 1.0000,  1.0000]],           [[-1.0000, -1.0000],          [-1.0000, -1.0000]],           [[ 1.0000,  1.0000],          [ 1.0000,  1.0000]]], grad_fn=)

 

这里分为两个组，计算均值与方差是按照分组后的数据进行计算的。

 

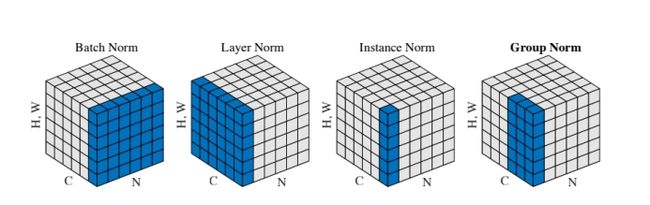
小结：四种Normalization的工作方式如下图：

BatchNorm：batch方向做归一化，算N*H*W的均值
LayerNorm：channel方向做归一化，算C*H*W的均值
InstanceNorm：一个channel内做归一化，算H*W的均值
GroupNorm：将channel方向分group，然后每个group内做归一化