Hermite(埃尔米特)插值法
Hermite(埃尔米特)插值法
Hermite插值法是解决数学建模中预测类问题的最常用的方法,可以有效的解决“已知数据”数量不够的问题。
但是,直接使用Hermite插值得到的多项式次数较高,也存在着“龙格现象(Runge phenomenon)”。因此,在实际应用中,往往使用分段三次Hermite插值多项式(PCHIP),来提高“模拟数据的准确性”。
这里要说明一下“龙格现象(Runge phenomenon)”,
龙格现象(Runge phenomenon)
简单的解释为:插值多项式的震荡,即在两段处波动极大,产生明显的震荡。
Hermite插值法的含义
保持插值曲线在节点处有切线(光滑),使得插值函数和被插值函数的密合程度更好。
不但要求在节点处上的函数值相等,而且还要求对应的导数值也相等,甚至要求高阶导数也相等,满足这种要求的插值多项式就是“Hermite插值多项式”。
Hermite插值原理
Hermite插值法的代码实现
Matlab中的pchip函数
在Matlab中,内置有Hermite插值多项式(PCHIP)函数
格式:“p=pchip(x,y,new_x)”
其中:x是已知的样本点的横坐标,y是已知的样本点的纵坐标,new_x是要插入处的横坐标。
因此,new_x可以是一个区间。
Matlab中的代码实现:
%插值算法 (常用)
%Hermite(埃尔米特)插值法
a=0;
a=input('请输入数据矩阵的行数:');
b=0;
b=input('请输入数据矩阵的列数:');
%初始化目标矩阵
c=zeros(a,b);
c=input('请依次输入数据矩阵:');
disp('数据矩阵:');
disp(c);
%确定插值区间
d=0;
d=input('请输入插值区间:');
%进行插值
e(1,:)=d;
[n,m]=size(c);
for i=2:n
e(i,:)=pchip(c(1,:),c(i,:),d);
end
%目标矩阵
disp('Hermite插值后的矩阵:');
disp(e);
Hermite插值法的例题应用
题目“第六届mathorcup大学生数学建模挑战赛A题目”中的数据:
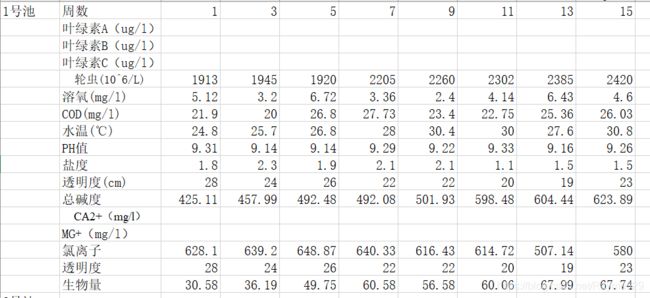
可以看出,题目中的数据只给出了“奇数周”,缺少“偶数周”的实验数据,因此需要进行“完善数据”。
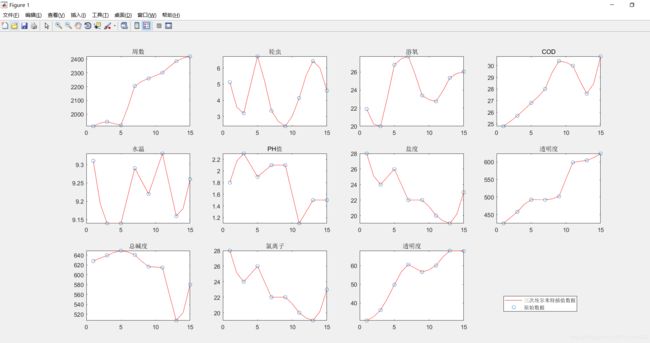
Matlab代码实现:
%第一种方法:Hermite(埃尔米特)插值法
%确定数据矩阵的大小
A=[1:15];
B(1,:)=A;
for i=2:12
B(i,:)=pchip(h(1,:),h(i,:),B(1,:));
end
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};
for j=2:12
subplot(3,4,j-1),
plot(B(1,:),B(j,:),'r');
hold on;
plot(h(1,:),h(j,:),'o');
axis([0 15,-inf,inf])
title(ylab{j-1})
end
legend('三次埃尔米特插值数据','原始数据','Location','SouthEast')