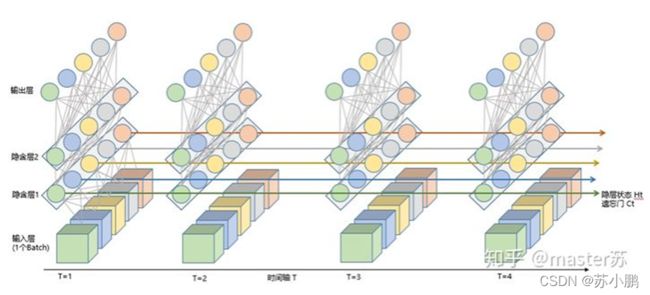
使用深度学习中的循环神经网络（LSTM）进行股价预测

tushare ID:468684

一、开发环境：

• 操作系统：Windows10
• 开发工具：PyCharm 2021.1.1 (Professional Edition)
• Python版本：Python3.6
• 深度学习框架TensorFlow2.6.2
• 数据来源：tushare
• 使用的库：tushare、Numpy、tensorflow.keras.layers 、matplotlib.pyplot 、pandas 、sklearn.preprocessing、sklearn.metrics 、math、tensorflow 、tensorflow.python.client 、os

二、TensorFlow安装与简介

略

三、LSTM简介与动手实现

 

四、tushare简介与使用

略

五、代码实现

使用TensorFlow API:tf.keras搭建网络六步法：

1. import
2. train，test
3. model=tf.keras.models.Sequential
4. model.compile
5. model.fit
6. model.summary

第一步，导入相关包

import numpy as np
from tensorflow.keras.layers import Dropout, Dense, LSTM
import tushare as ts
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
import tensorflow as tf
from tensorflow.python.client import device_lib
import os

第二步，获取数据并划分训练集和测试集

df1 = ts.get_k_data('股票代码', ktype='D', start='开始日期', end='结束日期')
datapath1 = "./股票代码.csv"
df1.to_csv(datapath1)

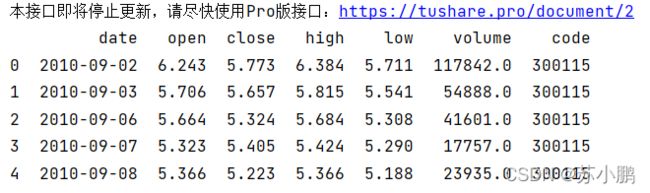
print(df1.head())

data = pd.read_csv('./股票代码.csv')  # 读取股票文件
training_set = data.iloc[0:2426 - 300, 2:3].values  # 前(2426-300=2126)天的开盘价作为训练集,表格从0开始计数，2:3 是提取[2:3)列，前闭后开,故提取出C列开盘价
test_set =data.iloc[2426 - 300:, 2:3].values  # 后300天的开盘价作为测试集

# 归一化
sc = MinMaxScaler(feature_range=(0, 1))  # 定义归一化：归一化到(0，1)之间
training_set_scaled = sc.fit_transform(training_set)  # 求得训练集的最大值，最小值这些训练集固有的属性，并在训练集上进行归一化
test_set = sc.transform(test_set)  # 利用训练集的属性对测试集进行归一化

x_train = []
y_train = []

x_test = []
y_test = []

第三步，model=tf.keras.models.Sequential

class MyModel(Model):

        def __init__(self):

        super(MyModel, self).__init__()         

        定义网络结构块

        def call(self, x):         

        调用网络结构块，实现前向传播

        return y

model = MyModel(）

第四步，model.compile

model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
              loss='mean_squared_error')  # 损失函数用均方误差
# 该应用只观测loss数值，不观测准确率，所以删去metrics选项，一会在每个epoch迭代显示时只显示loss值

checkpoint_save_path = "./checkpoint/LSTM_stock.ckpt"

if os.path.exists(checkpoint_save_path + '.index'):
    print('-------------load the model-----------------')
    model.load_weights(checkpoint_save_path)

cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
                                                 save_weights_only=True,
                                                 save_best_only=True,
                                                 monitor='val_loss')

第五步，model.fit

history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
                    callbacks=[cp_callback])

第六步，model.summary

model.summary()

此外，还可以loss可视化

file = open('./weights_changyingjingmi.txt', 'w')  # 参数提取
for v in model.trainable_variables:
    file.write(str(v.name) + '\n')
    file.write(str(v.shape) + '\n')
    file.write(str(v.numpy()) + '\n')
file.close()

loss = history.history['loss']
val_loss = history.history['val_loss']

plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()

################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从（0，1）反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从（0，1）反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='XXXXX Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted XXXXX Stock Price')
plt.title('Changyingjingmi Stock Price Prediction(LSTM)')
plt.xlabel('Time')
plt.ylabel('XXXXX Stock Price')
plt.legend()
plt.show()

##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值-真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE]    (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值）
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)

运行效果截图：

---

---

---

 

---

 

 参考文献：

1.Sepp Hochreiter,Jurgen Schmidhuber.LONG SHORT-TERM MEMORY.Neural Computation,December 1997

2.浙江大学慕课《深度学习》，胡浩基

3.北京大学慕课《人工智能实践：TensorFlow笔记》，曹健

4.知乎《LSTM模型结构的可视化》，master苏

5.复旦大学慕课《深度学习及其应用》，赵卫东，董亮

6.浙江大学慕课《人工智能：模型与算法》，吴飞

7.微信公众号数盟，《深度解析LSTM神经网络的设计原理》