GLSL-TBN矩阵

TBN矩阵

一、简述

1.1 TBN矩阵作用

我们研究一个矩阵的时候通常需要了解一个矩阵是从哪一个空间或者说矩阵而来的。如果搜索一下TBN矩阵运算公式可以发现其决定于物体坐标系下的顶点和纹理坐标系下的纹理坐标。想到这里我们需要明确TBN运算的输入和输出是什么。

• 先说输入：输入是一张纹理的rgb，分别代表纹理坐标系下的xyz轴上的分量，而TBN是一一对应于xyz的。
• 再说输出：输出是物体坐标系下的法线向量。

然后我们很容易得出了结论，TBN是将一个点从纹理空间变换到物体空间的一个矩阵。这么解释对吗？纹理空间、切线空间、物体空间，如何通过个矩阵找到对应关系。TBN的坐标轴的坐标值是物体空间下的，所以TBN其实就是从切线空间到物体空间的对应关系。而根据公式已经将纹理空间的xyz和TBN建立了对应关系，那么即可通过rgb在TBN空间下找到一条向量。所以纹理坐标对TBN：有求解关系，无对应变换关系。这样即通过公式将纹理空间和切线空间合二为一，剩下的就好理解了。

因此TBN构成一个变换矩阵，即每一个坐标轴是对应矩阵的一列。就可将切线空间下的法线变换到物体空间下的法线。

1.2 切线空间

法线贴图中存储的法线最初是定义在世界空间中，但在实际中，这种方式很少见，因为只要物体移动，法线贴图则不再有效。另一种方式就是将法线存储在物体的局部空间中，物体可以进行刚体变换（平移，旋转，缩放），法线贴图依旧有效，但是这种方法并不能应对任何方式的变换，并且法线贴图不能在不同物体进行复用，增加了美工的负担。所以，现在现在普遍采用的解决方案是将法线存储在切线空间中。

简单的来说，切线空间可以理解为纹理空间的u，v方向和法向量n，这3个方向构成了切线空间，一般使用T、B和N表示，如图3所示。具体解释见http://blog.csdn.net/bonchoix/article/details/8619624，这个博客解释的很好，没见过的童鞋可以看一看，第一次理解可能会有点困难。
　　
直观地讲，模型顶点中的纹理坐标，就定义于切线空间。普通2维纹理坐标包含U、V两项，其中U坐标增长的方向， 即切线空间中的tangent轴，V坐标增加的方向，为切线空间中的bitangent轴。模型中不同的三角形，都有对应的切线空间，其tangent轴和bitangent轴分别位于三角形所在平面上，结合三角形面对应的法线，我们称tangant轴（T）、bitangent轴（B）及法线轴（N）所组成的坐标系，即切线空间（TBN）。

在立方体中，每个面都有对应的切线空间，每个面由两个三角形组成，该两个三角形中的纹理坐标就基于相应的切线空间。

1.3 纹理坐标与位置坐标的关系

纹理坐标与位置坐标，可以通过切线空间联系起来。如下图所示：

该图显示了一个三角形及其所在的切线空间。已知该三角形三个顶点的位置坐标：V0, V1,V2, 以及对应的纹理坐标：(u0,v0,), (u1, v1), (u2, v2)。 定义三角形的两条边为E0 = V1 –V0，E1= V2 – V0，对应的纹理坐标差值：(t1, b1) = (u1 – u0, v1– v0)， (t2, b2) = (u2 – u0, v2– v0)。 我们有如下关系式：

E0 =t1T+ b1B

E1 = t2T+ b2B

二、推导应用

一条法线是一个三维向量，一个三维向量由x, y, z等3个分量组成，在法线贴图中，把(x, y, z)当作RGB3个颜色的值存储（如图2），并将其每个分量映射到[-1, 1]。例如，对于x, y, z各有8位的纹理，[0， 128， 255]表示法向量(-1, 0, 1)。利用彩色通道存储法线贴图如下：

在使用法线贴图（normal mapping）等技术时时，最关键的一个矩阵就是TBN矩阵，该矩阵用于将存储在纹理空间中的法向量转换到模型空间中（实际使用相反，为了减少计算量，是将光线从模型空间转换到了纹理空间，然后计算反射光线，因为光线条数远远少于法向量数目）。

下图展示法线贴图的含义，图中的蓝色部分为一块法线纹理，上面的黑色小木棒（灵魂手绘）是每个像素的rgb代表的法线向量。就像一块海绵上插了无数歪歪扭扭的针一样……这样当计算反射光线时，这些法向量模拟凹凸不平的表面，最后产生真实的感觉。

2.1 两空间转换矩阵原理

首先考虑向量空间中坐标表示的问题，给定一个三维坐标系的一组基：(向量X，向量Y，向量Z)，那么该坐标系中的任意向量A(a1,a2,a3)的坐标的含义为：

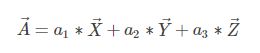
，即A用基向量表示时各分量的值。如果再给定另外一个坐标系的一组基:：(向量U，向量V，向量W)，并且给出XYZ向量在这个坐标系中的表示xyz，那么就可以很方便得到A向量在第二个坐标系中的表示，(a1,a2,a3)∗[x,y,z]T。因此，[x,y ,z ]T可以看作是这两个空间的转换矩阵。

2.2 TBN矩阵推导

如上图所示，假定△ABC纹理映射到模型中△abc这块三角形上，纹理中存储的rgb分量代表该点处法线在纹理空间中的坐标，我们要将左边的纹理空间中的法向量转换到右边的模型空间中（这里先只讨论uv二维的坐标，第三维直接取模型空间的法向量即可），已知顶点的UV坐标，模型坐标以及法向量，根据上面的讨论，现在要求出U ,V这两个向量基在模型空间中的坐标，即右边 T,B的坐标。我们可以列出一个方程组：

然后解出T,B即可。加上第三维坐标时，一般会选择垂直于TB平面的法向量N，这个向量是已知的。最后再将T,B,N归一化，就得到了转换矩阵。

但是开头说过了，实际我们使用的变换是将光线从模型空间变换到纹理空间，因此要求的实际是逆过程的转换矩阵，好在TBN矩阵是正交阵，转置一下就得到了[T,B,N]−1。