推荐算法论文笔记01-《Sequential Recommendation with Graph Neural Networks》

一、论文概括

来自于清华大学发表于2021SIGIR的一篇论文，主要内容是通过计算用户在会话中的主要兴趣并计算兴趣聚簇来解决顺序推荐问题。

二、介绍

1. 顺序推荐能够捕获用户（兴趣）的演变和动态偏好
2. 现有工作从三个角度解决快速变化短期偏好建模问题：

• 早期采用预设规则或注意机制为历史交互的项目分配时间衰减的权重,
• 第二类利用递归神经网络来总结行为序列，但是难以建模长期依赖关系，
• 最近的解决方案联合建模长期和短期利益，以避免忘记长期利益

3. 根据以上，存在以下两方面的问题：

• 长序列中的用户行为反映了隐式的和有噪声的偏好信号
• 由于用户偏好的多样性，用户偏好总是随着时间的推移而变化

对于上述问题，作者提出SURGE网络(Sequential Recommendation with Graph Neural Networks)：（1）从新角度解决顺序推荐,考虑隐信号行为和快速变化的偏好（2）通过物品-物品兴趣图,使用GNN网络将隐式信号转化为显式信号,设计动态池化来过滤和保留主要偏好以供推荐

三、方法

浪涌模型由以上四个部分组成，接下来将一个一个地详细阐述：

A.Interest Graph Construction（兴趣图构建）

通过基于度量学习将松散的项目序列重构为紧密的项目-项目兴趣图，作者明确地整合和区分了长期用户行为中不同类型的偏好，作者将松散的项目序列转换为紧密的项目-项目兴趣图,但是项目对之间的稀疏性不足以为每个用户生成连通图，因此作者提出了一种基于度量学习的新方法：

原始图形结构

通过将每个用户的交互历史表示为一个图表，可以更容易地区分他们的核心兴趣和外围兴趣。核心兴趣节点的连接程度高于外围兴趣节点具有更高的程度，相似兴趣的频率越高，子图越密集越大。这样，就构造了一个先验框架，即邻居节点相似，密集子图是用户的核心兴趣。

节点相似度度量学习

作者将图学习问题转化为节点相似度度量学习，并与下游推荐任务进行联合训练，作者为了平衡表达性和复杂性，我们采用加权余弦相似度作为度量函数，公式如下：
$$M_{ij}=\cos \left(\mathbf{w}\odot h_i,\mathbf{w}\odot h_j\right)$$
$$M_{ij}^{\delta }=\cos \left({\mathbf{w}}_{\delta }\odot h_i,{\mathbf{w}}_{\delta }\odot h_j\right),M_{ij}=\frac{1}{\delta }\sum _{\delta =1}^{\varphi }{M}_{ij}^{\delta }$$

通过ε-稀疏化来实现图的稀疏化

从邻接矩阵M中通过只考虑具有最重要连接的节点对来提取对称稀疏非负邻接矩阵A。为了使提取阈值的超参数不敏感，且不破坏图的稀疏性分布，作者采用了对整个图的相对排序策略。具体地说屏蔽掉M中小于非负阈值的元素，这是通过对M中的度量值进行排序得到的。
$$A_{ij}=\{\begin{array}{ll}1,& M_{ij}>={\mathrm{Rank}}_{\epsilon n^2}(M)\\ 0,& \text{ otherwise }\end{array}$$

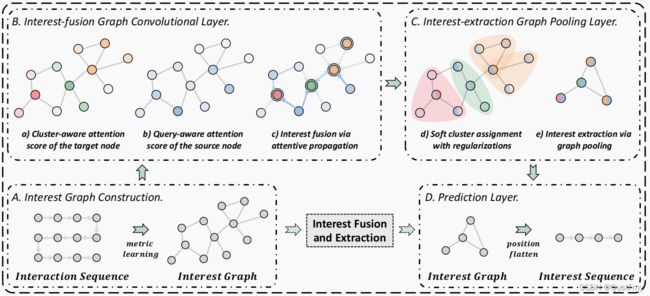
B.Interest-fusion Graph Convolutional Layer(兴趣融合图卷积层)

为了将弱信号收集到能够准确反映用户偏好的强信号，在构建的图中聚合信息。

通过图形注意卷积进行兴趣融合

提出了一个感知集群（cluster-aware）和查询（query-aware）的图注意卷积层，用来感知信息聚合过程中用户的核心兴趣，计算对齐得分Eij来映射目标节点vi在其邻居节点vj上的重要性：
$$h_i^{\prime }=\sigma \left({\mathbf{W}}_{\mathbf{a}}\cdot \text{ Aggregate }\left(E_{ij}\ast h_j\mid j\in {\mathcal{N}}_i\right)+h_i\right)$$

这里的聚合函数作者采用了和函数，为了稳定注意机制的学习过程，作者采用了多头注意力：
$$h_i^{\prime }={\Vert }_{\delta =1}^{\varphi }\sigma \left({\mathbf{W}}_{\mathbf{a}}^{\delta }\cdot \text{ Aggregate }\left(E_{ij}^{\delta }\ast h_j\mid j\in {\mathcal{N}}_i\right)+h_i\right)$$

集群和查询感知的注意

在整合兴趣时加强重要信号削弱噪声信号，在消息传递过程中，利用注意系数来重新分配边缘信息的权重。注意机制考虑了以下两个方面：
首先，作者假设目标节点vi的邻域将形成一个簇，并将图中的目标节点视为簇c(vi)的medoid。将目标节点vi的k跳邻域定义为聚类的接受域。集群中嵌入的所有节点的平均值$h_i$的平均值表示集群的平均信息。为了确定目标节点是否为聚类的中心，我们使用目标节点的嵌入及其聚类的嵌入来计算以下注意力得分，
$${\alpha }_i={\text{ Attention }}_c\left({\mathbf{W}}_{\mathbf{c}}{h}_i\Vert h_{i_c}\Vert {\mathbf{W}}_{\mathbf{c}}{h}_i\odot h_{i_c}\right)$$
考虑源节点嵌入hj与目标项目嵌入ht之间的相关性。如果源节点与查询项的相关性更强，那么它在向目标节点的聚合中的权重将更重要，反之亦然。只保留相关的信息，而在聚合过程中，不相关的信息将会被丢弃。
$${\beta }_j={\text{ Attention }}_q\left({\mathbf{W}}_{\mathbf{q}}{h}_j\Vert h_t\Vert {\mathbf{W}}_{\mathbf{q}}{h}_j\odot h_t\right)$$
为了使系数易于在不同节点之间进行比较，使用softmax函数对j的所有选择进行归一化
$$E_{ij}={\mathrm{softmax}}_j\left({\alpha }_i+{\beta }_j\right)=\frac{\exp \left({\alpha }_i+{\beta }_j\right)}{{\sum }_{k\in {\mathcal{N}}_i}\exp \left({\alpha }_i+{\beta }_k\right)}$$

C.Interest-extraction Graph Pooling Layer

使用图池方法来进一步提取融合的信息,目的是合理地缩小图的大小。通过对所构造的图结构的粗化，将松散兴趣转化为紧密兴趣，并保持其分布。

通过图形池提取兴趣

作者将n个项目的表征用S矩阵分为m个类,