Python实现快速计算24点游戏的示例代码

目录

• 24 点游戏规则
• 回溯算法计算思路
• 生成表达式

24 点游戏规则

有4个范围在 [1,9] 的数字，通过「加、减、乘、除」四则运算能够获得24，认为有解。

4个范围在 [1,9] 的数字能够产生495种可能，其中404中组合情况都是有解的，有解概率高达81.62%。

下面我们用python来验证它，首先计算组合数：

from scipy.special import comb

comb(9, 4, repetition=True)

495.0

可以看到python计算出9个数字有重复的组合情况数是495。

下面我们需要一个方法，判断4个数字能否组合成为24点，这里我采用回溯算法进行计算。

回溯算法计算思路

首先从4个数字中选择2个数字，然后再选择一种运算操作，然后用得到的结果取代选出的2个数字。然后在剩下的3个数字中，进行同样的操作。依次类推，最终计算到只剩一个数字，看结果是否为24即可。

开始编码：

from operator import add, mul, sub, truediv

ops = [add, mul, sub, truediv]


def judgePoint24(nums) -> bool:
    if not nums:
        return False
    n = len(nums)
    if n == 1:
        return round(nums[0], 3) == 24
    for i, j in permutations(range(n), 2):
        # 选2个数字
        x, y = nums[i], nums[j]
        newNums = []
        # 选择加减乘除 4 种运算操作之一，用得到的结果取代选出的 2 个数字
        for k, z in enumerate(nums):
            if k != i and k != j:
                newNums.append(z)
        for k in range(4):
            if k < 2 and i > j:
                # 加法和乘法满足交换律,跳过第二种顺序
                continue
            if k == 3 and round(y, 3) == 0:
                # 除法运算除数不能为0
                continue
            newNums.append(ops[k](x, y))
            if judgePoint24(newNums):
                return True
            newNums.pop()
    return False

然后我们遍历所有的组合进行判断：

from scipy.special import comb

​​​​​​​total = int(comb(9, 4, repetition=True))
cnt = sum(judgePoint24(nums)
          for nums in combinations_with_replacement(range(1, 10), 4))
print(f'{cnt}/{total}={cnt/total:.2%}')

最终一秒内计算出结果：

生成表达式

下面我们加大难度，要求在求解时，能够同时返回可行的表达式。暴力遍历固然可以实现，但是耗时太长，能否在这种回溯算法的基础上实现呢？

我的思路是加个变量记录每次的选择，最终再通过一定的技巧进行还原，最终编码：

from operator import add, mul, sub, truediv
from itertools import permutations, combinations_with_replacement
from collections import defaultdict


def judgePoint24(nums) -> bool:
    ops = [add, mul, sub, truediv]
    op_char = "+*-/"
    record = []

    def solve(nums) -> bool:
        if not nums:
            return False
        n = len(nums)
        if n == 1:
            return round(nums[0], 3) == 24
        for i, j in permutations(range(n), 2):
            # 选2个数字
            x, y = nums[i], nums[j]
            newNums = []
            # 选择加减乘除 4 种运算操作之一，用得到的结果取代选出的 2 个数字
            # 先添加未选择的数字
            newNums = [z for k, z in enumerate(nums) if k not in (i, j)]
            for k in range(4):
                if k < 2 and i > j:
                    # 加法和乘法满足交换律,跳过第二种顺序
                    continue
                if k == 3 and (round(y, 3) == 0):
                    # 除法运算除数不能为0
                    continue
                v = ops[k](x, y)
                newNums.append(v)
                record.append(([round(x, 3), round(y, 3)],
                              op_char[k], round(v, 3)))
                if solve(newNums):
                    return True
                newNums.pop()
                record.pop()
        return False
    flag = solve(nums)
    if not flag:
        return False, ""
    cache = defaultdict(list)
    for ns, op, v in record:
        for i in range(2):
            if cache[ns[i]]:
                ns[i] = "("+cache[ns[i]].pop()+")"
        a, b = ns
        cache[v].append(f"{a}{op}{b}")
    return flag, cache[24][0]+"=24"

然后开始遍历：

total = cnt = 0
for nums in combinations_with_replacement(range(1, 10), 4):
    total += 1
    r, expression = judgePoint24(nums)
    if r:
        print(expression, end="\t")
        cnt += 1
        if cnt % 8 == 0:
            print()
print()
print(f'{cnt}/{total}={cnt/total:.2%}')

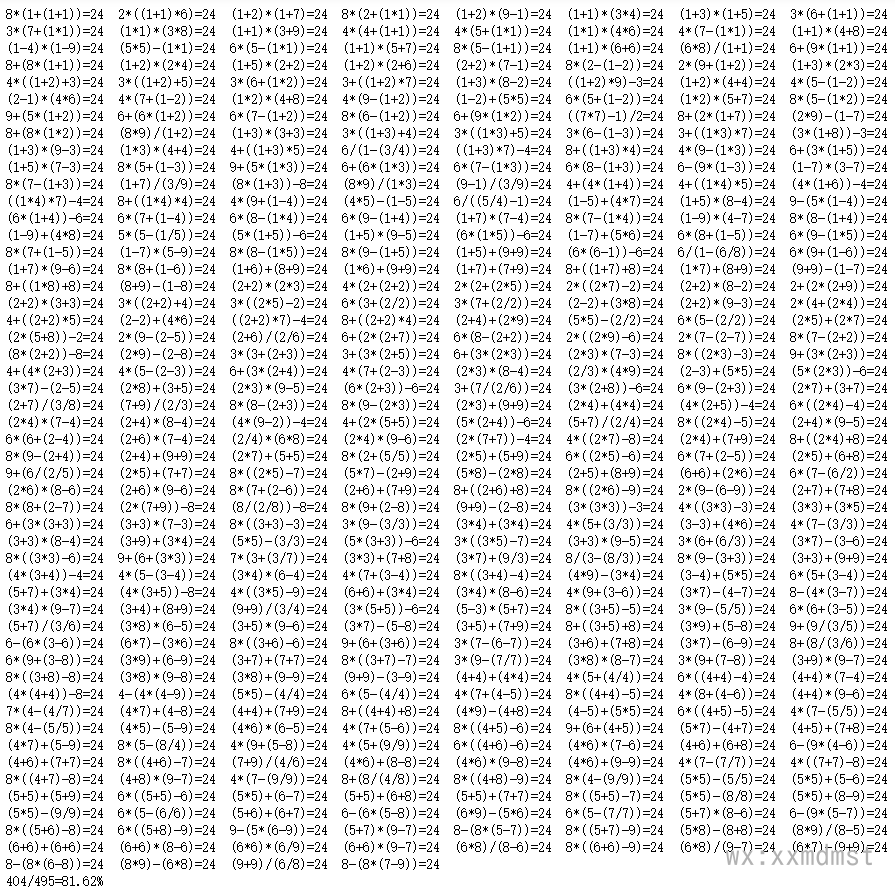
最终结果：

可以看到，我们已经得到了404个24点的有效解表达式。

到此这篇关于Python实现快速计算24点游戏的示例代码的文章就介绍到这了,更多相关Python计算24点游戏内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家！